
平面向量数量积的运算律
1.交换律:a × b = b × a
证:设a,b夹角为q,则a × b = |a||b|cosq,b × a = |b||a|cosq
∴a × b = b × a
7.判断下列各题正确与否:
1°若a = 0,则对任一向量b,有a×b = 0 ( √ )
2°若a ¹ 0,则对任一非零向量b,有a×b ¹ 0 ( × )
3°若a ¹ 0,a×b = 0,则b = 0 ( × )
4°若a×b = 0,则a 、b至少有一个为零 ( × )
5°若a ¹ 0,a×b = a×c,则b = c ( × )
6°若a×b = a×c,则b = c当且仅当a ¹ 0时成立 ( × )
7°对任意向量a、b、c,有(a×b)×c ¹ a×(b×c) ( × )
8°对任意向量a,有a2 = |a|2 ( √ )
5.两个向量的数量积的性质:
设a、b为两个非零向量,e是与b同向的单位向量
1°e×a = a×e =|a|cosq;2°a^b Û a×b = 0
3°当a与b同向时,a×b = |a||b|;当a与b反向时,a×b = -|a||b|
特别的a×a = |a|2或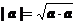
4°cosq =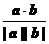 ;5°|a×b| ≤ |a||b|
;5°|a×b| ≤ |a||b|
4.向量的数量积的几何意义:
数量积a×b等于a的长度与b在a方向上投影|b|cosq的乘积
3.“投影”的概念:作图
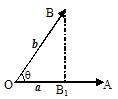
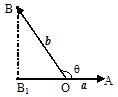
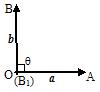
定义:|b|cosq叫做向量b在a方向上的投影
投影也是一个数量,不是向量;当q为锐角时投影为正值;当q为钝角时投影为负值;当q为直角时投影为0;当q = 0°时投影为 |b|;当q = 180°时投影为 -|b|
1.两个非零向量夹角的概念
已知非零向量a与b,作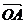 =a,
=a,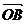 =b,则∠AOB=θ(0≤θ≤π)叫a与b的夹角
=b,则∠AOB=θ(0≤θ≤π)叫a与b的夹角
|
(0≤θ≤π)并规定0与任何向量的数量积为0
18..解:(Ⅰ)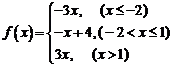 ,令
,令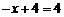 或
或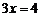 ,
,
得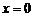 ,
,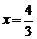 ,所以,不等式
,所以,不等式 的解集是
的解集是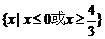 .-------6分
.-------6分
(Ⅱ)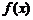 在
在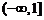 上递减,
上递减,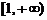 递增,所以,
递增,所以,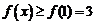 ,
,
由于不等式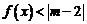 的解集是非空的集合,所以
的解集是非空的集合,所以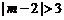 ,
,
解之,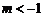 或
或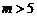 ,即实数
,即实数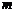 的取值范围是
的取值范围是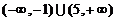 .------10分
.------10分
17.解:(Ⅰ)由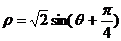 得,
得,
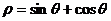 ,两边同乘
,两边同乘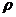 得,
得,
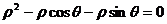 ,
,
再由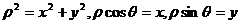 ,
,
得曲线C的直角坐标方程是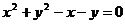 …………5分
…………5分
(Ⅱ)将直线参数方程代入圆C方程得,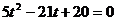
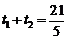 ,
,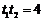 ,
,
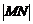
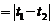
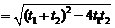
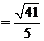 .-------10分
.-------10分
16. 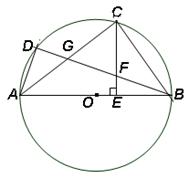 证明:(Ⅰ)∵
证明:(Ⅰ)∵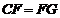 ,
,
∴ 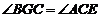 ,
,
∵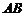 是
是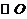 的直径,
的直径,
∴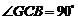
∵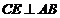
∴ 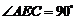 ,
,
∴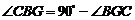
15.证明::(法一:综合法)∵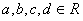 ,
,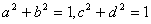
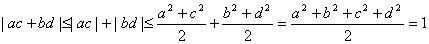
∴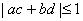
(法二:综合法)∵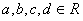 ,
,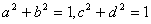
∴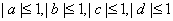
设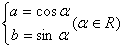 ,
,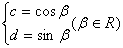
∴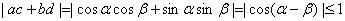
∴原不等式成立。
(法三:比较法)先证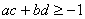
∵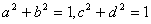
∴
=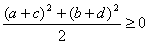
∴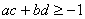 再证
再证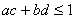
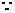
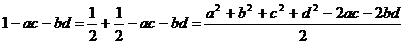
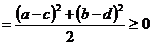
∴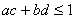 综上所述知
综上所述知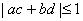
(法四:分析法)
要证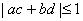
只要证
只需证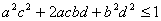
∵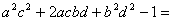
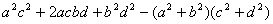
=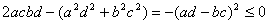
∴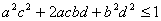
∴原不等式成立。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com