
25. He _____ for a taxi, so he walked home.
A. had some money B. had any money
C. didn’t have some money D. didn’t have any money
24. --- I’m going to Hawaii with my aunt this month for my holiday.
---________.
A .Have a good time B. Best wishes to you
C. Congratulations D. Please go
23. Do you enjoy _______ books about history?
A. seeing B. reading C. looking D. to read
22. Listen ! Someone _______ the door.
A. knocks on B. is knocking C. is knocking on D. knock on
Ⅴ. 单项填空(15分)
21. Once upon a time, there _______ a girl ________ Gina in a village.
A. is, called B. was , call C. was , called D. is, call
Ⅰ.根据所听到的句子的先后顺序,给图片排序,句子读两遍。(5分)
A B C D E





Ⅱ.情景反应,选出能回答你所听到的句子的选项。(5分)
6. A. In 1996. B. In Nanjing. C. 13 years old.
7. A .I’m sorry. B .Goodbye. C .Yes, I’d like some apples.
8. A .Yes, I do. B.Yes, I am. C .Yes, it is.
9. A. She is watching TV. B. She likes dancing. C. She will do her homework.. 10. A. Watched TV. B. Yes, she did. C. No ,she wasn’t.
Ⅲ. 听对话,选答案。你将听到五段对话,每段对话读两遍。请在每小题所给的A B C三个选项中选出一个最佳选项。(5分)
11. How does David like to travel?
A. By train B. By air C. By bike
12. Who did the boy go to visit ?
A .his aunt B .his uncle C .her uncle
13. Where is the fruit shop ?
A .It’s near the hospital . B. It’s next to a shop . C. It’s near the school.
14. Who runs slowest?
A. Lin Tao. B. Mr Hu. C. Lucy.
15. Where was the man last year?
A. In Shanghai. B. In Tianjin. C. In Beijing.
Ⅳ. 短文理解(共5小题;每小题1分,满分5分)
你将听到一篇短文,短文后有五个小题。请根据短文内容,在每小题所给的A、B、C三个选项中选出一个最佳选项。短文读两遍。
16. John is Jim’s _________.
A. friend B. brother C. classmate
17. What did their parents want them to do ?
A. To do their homework. B. To buy some books. C. To clean their home.
18. Where did their parents go ?
A. They went to work. B. They went to a park. C. Then went to a party.
19. Who was ill?
A. Jim. B. John. C. Nobody.
20. What do you think of Jim and John?
A. Very good. B. Very lazy(懒惰). C. Not clever.
1下列叙述不正确的是( )
A向量的数量积满足交换律 B向量的数量积满足分配律
C向量的数量积满足结合律 Da·b是一个实数
2已知|a|=6,|b|=4,a与b的夹角为60°,则(a+2b)·(a-3b)等于( )
A72 B-72 ?C36 ?D-36
3|a|=3,|b|=4,向量a+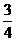 b与a-
b与a-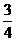 b的位置关系为( )
b的位置关系为( )
A平行
B垂直 C夹角为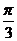 ?D不平行也不垂直
?D不平行也不垂直
4已知|a|=3,|b|=4,且a与b的夹角为150°,则(a+b)2=
5已知|a|=2,|b|=5,a·b=-3,则|a+b|=______,|a-b|=
6设|a|=3,|b|=5,且a+λb与a-λb垂直,则λ=
例1 已知a、b都是非零向量,且a + 3b与7a - 5b垂直,a - 4b与7a - 2b垂直,求a与b的夹角
解:由(a + 3b)(7a - 5b) = 0 Þ 7a2 + 16a×b -15b2 = 0 ①
(a - 4b)(7a - 2b) = 0 Þ 7a2 - 30a×b + 8b2 = 0 ②
两式相减:2a×b = b2
代入①或②得:a2 = b2
设a、b的夹角为q,则cosq =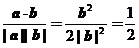 ∴q = 60°
∴q = 60°
例2 求证:平行四边形两条对角线平方和等于四条边的平方和
解:如图:
 ABCD中,
ABCD中,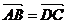 ,
, ,
,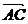 =
=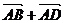
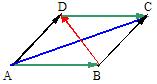 ∴|
∴|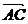 |2=
|2=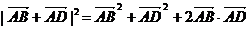
而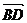 =
=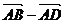
∴|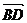 |2=
|2=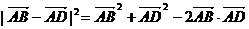
∴|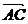 |2
+ |
|2
+ |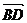 |2
= 2
|2
= 2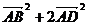 =
= 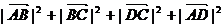
例3 四边形ABCD中,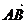 =a,
=a,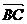 =b,
=b,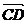 =с,
=с,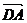 =d,且a·b=b·с=с·d=d·a,试问四边形ABCD是什么图形?
=d,且a·b=b·с=с·d=d·a,试问四边形ABCD是什么图形?
分析:四边形的形状由边角关系确定,关键是由题设条件演变、推算该四边形的边角量
解:四边形ABCD是矩形,这是因为:
一方面:∵a+b+с+d=0,
∴a+b=-(с+d),∴(a+b)2=(с+d)2
即|a|2+2a·b+|b|2=|с|2+2с·d+|d|2
由于a·b=с·d,
∴|a|2+|b|2=|с|2+|d|2①
同理有|a|2+|d|2=|с|2+|b|2②
由①②可得|a|=|с|,且|b|=|d|即四边形ABCD两组对边分别相等
∴四边形ABCD是平行四边形
另一方面,由a·b=b·с,有b(a-с)=0,而由平行四边形ABCD可得a=-с,代入上式得b·(2a)=0
即a·b=0,∴a⊥b也即AB⊥BC
综上所述,四边形ABCD是矩形
评述:(1)在四边形中,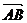 ,
,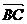 ,
,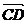 ,
,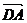 是顺次首尾相接向量,则其和向量是零向量,即a+b+с+d=0,应注意这一隐含条件应用;
是顺次首尾相接向量,则其和向量是零向量,即a+b+с+d=0,应注意这一隐含条件应用;
(2)由已知条件产生数量积的关键是构造数量积,因为数量积的定义式中含有边、角两种关系
3.分配律:(a + b)×c = a×c + b×c
在平面内取一点O,作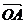 = a,
= a, 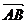 = b,
= b,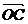 = c,
= c,
∵a + b (即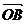 )在c方向上的投影等于a、b在c方向上的投影和,
)在c方向上的投影等于a、b在c方向上的投影和,
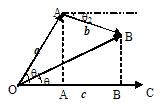 即 |a
+ b|
cosq = |a|
cosq1 + |b| cosq2
即 |a
+ b|
cosq = |a|
cosq1 + |b| cosq2
∴| c | |a + b| cosq =|c| |a| cosq1 + |c| |b| cosq2
∴c×(a + b) = c×a + c×b 即:(a + b)×c = a×c + b×c
说明:(1)一般地,(a·b)с≠a(b·с)
(2)a·с=b·с,с≠0a=b
(3)有如下常用性质:a2=|a|2,
(a+b)(с+d)=a·с+a·d+b·с+b·d
(a+b)2=a2+2a·b+b2
2.数乘结合律:( a)×b =
a)×b = (a×b) = a×(
(a×b) = a×( b)
b)
证:若 > 0,(
> 0,( a)×b =
a)×b = |a||b|cosq,
|a||b|cosq,
 (a×b) =
(a×b) = |a||b|cosq,a×(
|a||b|cosq,a×( b)
=
b)
= |a||b|cosq,
|a||b|cosq,
若 < 0,(
< 0,( a)×b =|
a)×b =| a||b|cos(p-q) = -
a||b|cos(p-q) = - |a||b|(-cosq) =
|a||b|(-cosq) = |a||b|cosq,
|a||b|cosq,
 (a×b) =
(a×b) = |a||b|cosq,
|a||b|cosq,
a×( b)
=|a||
b)
=|a|| b|cos(p-q) = -
b|cos(p-q) = - |a||b|(-cosq) =
|a||b|(-cosq) = |a||b|cosq
|a||b|cosq
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com