3、作常用辅助线的方法。

[课后作业]

班级　　 姓名　　　　　 学号　　　

2、掌握了切线的性质；

1、理解切线的判定方法以及适用情况；

6.总结

切线的性质定理：圆的切线垂直于经过切点的半径 。

(3)小结切线的性质：

性质一：直线与圆唯一公共点

　　 性质二：数量关系--“d = r”

性质三：圆的切线垂直于经过切点的半径 。

例2.如图，AB是⊙O的直径，AC＝AB，⊙O交BC于D。DE⊥AC于E，DE是⊙O的切线吗？为什么？

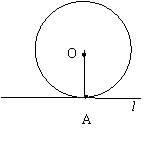
5.切线性质的探索

(1)如果已知直线与圆相切，那么能得到哪些结论？

　　 性质一：直线与圆唯一公共点

　　　 性质二：数量关系--“d = r”

(2)如图，直线l与⊙O相切于点A，直线l与

O A是否一定垂直？为什么？

4.典型例题

例1.如图，O是∠ABC的平分线上的一点，OD⊥BC于D，

以O为圆心、OD为半径的圆与AB相切吗？为什么？

例题小结：

①常用辅助线--判定直线与圆相切时，作出半径是常用辅助线

②当直线与圆的公共点已知时，用判定定理，即只要证明直线与过公共点的半径垂直即可证明是切线；当直线与圆公共点未知时，用“d = r” 证明直线是圆的切线。

3.交流

判定直线与圆相切的方法：

方法一：定义--唯一公共点

　 方法二：数量关系--“d = r”

　 方法三：判定定理--2个条件：

①直线与圆有公共点、

②直线与过公共点的半径垂直。

2.总结

切线的判定定理：经过半径的外端并且垂直于这条半径的直线是圆的切线。

1.思考

(1)在上述画图过程中，你画图的依据是什么？(“d = r”)

(2)根据上述画图，你认为直线l具备什么条件就是⊙O的切线了？

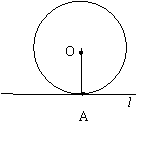
3、如图， A为⊙O上一点，你能经过

点A画出⊙O的切线吗？