
6.过直线l1:A1x+B1y+C1=0,l2:A2x+B2y+C2=0交点的直线系方程为:
A1x+B1y+C1+λ(A2x+B2y+C2)=0(λ∈R)(除l2外)。
5.直线方程的五种形式
点斜式: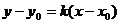 , (斜率存在)
, (斜率存在)
斜截式: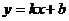 (斜率存在)
(斜率存在)
两点式: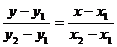 ,(不垂直坐标轴)
,(不垂直坐标轴)
截距式: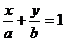 (不垂直坐标轴,不过原点)
(不垂直坐标轴,不过原点)
一般式: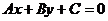
4.直线的倾斜角、斜率、方向向量都是刻划、描述直线的倾斜成度的。
每一条直线都有倾斜角和方向向量,但不是每一条直线都有斜率,要注意三者之间的内在联系。
3.直线的方向向量:设F1(x1,y1)、F2(x2,y2)是直线上不同的两点,则向量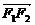 =(x2-x1,y2-y1)称为直线的方向向量
=(x2-x1,y2-y1)称为直线的方向向量
向量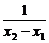
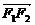 =(1,
=(1,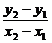 )=(1,k)也是该直线的方向向量,k是直线的斜率.特别地,垂直于
)=(1,k)也是该直线的方向向量,k是直线的斜率.特别地,垂直于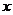 轴的直线的一个方向向量为
轴的直线的一个方向向量为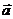 =(0,1)
=(0,1)
2.直线的斜率:倾斜角α不是90°的直线,它的倾斜角的正切叫做这条直线的斜率,常用k表示,即k=tanα(α≠90°)
倾斜角是90°的直线没有斜率;倾斜角不是90°的直线都有斜率,斜率的取值范围是(-∞,+∞)
1.直线的倾斜角:在平面直角坐标系中,对于一条与x轴相交的直线,如果把x轴绕着交点按逆时针方向旋转到和直线重合时所转的最小正角记为α,那么α就叫做直线的倾斜角
当直线和x轴平行或重合时,我们规定直线的倾斜角为0°
可见,直线倾斜角的取值范围是0°≤α<180°
3.能根据条件熟练地求出直线方程.
2.掌握直线方程的点斜式、两点式和直线方程的一般式,掌握由一点和斜率导出直线方程的方法;
1.理解直线的倾斜角和斜率的概念,掌握过两点的直线的斜率公式,
31.(15分) I、为了研究在大豆种子萌发和生产过程中糖类和蛋白质的相互关系,某研究小组在25℃、黑暗、无菌、湿润的条件下萌发种子,然后测定在不同的种子和幼苗中相关物质的含量,结果如图所示:
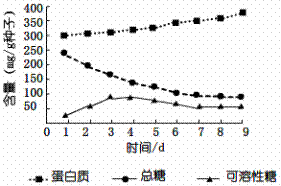
(1)在观察时间内,图中可溶性糖含量的变化是 ,
萌发前营养物质主要储存在大豆子的 中,此结构最初由 发育而来。
(2)上图表明,糖类和蛋白质之间的关系是 。
糖类在 过程中产生一些中间产物,可以通过 作用生成相对应的 。
(3)如果在同样条件下继续培养,预测上图曲线的最终变化是 。其原因是 。
II 、在上述定量测定之前,进行了蛋白质含量变化的预测实验,请填充实验原理;判断实验步骤中划线部分是否正确,并更正错误之处;写出实验结果。
(1)实验原理:蛋白质 ,其颜色深浅与蛋白质含量成正比。
(2)实验步骤:
①将三份等量大豆种子分别萌发1、5、9天后取出,各加入适量蒸馏水,研碎、提取、定容后离心得到蛋白质制备液;
②取3支试管,编号1、2、3,分别加入等量的萌发1、5、9蛋白质制备液;
③在上述试管中各加入等量的双缩脲试剂A和B(按比例配制)的混合液,振荡均匀后, a
在沸水中加热观察颜色变化。
b
a: 。
b: 。
(3)实验结果:
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com