
1直线的倾斜角、斜率及直线在坐标轴上的截距是刻画直线位置状态的基本量,应正确理解和运用;
2.直线方程有五种形式.其中点斜式、两点式、斜截式、截距式都是直线方程的特殊形式,点斜式是最基本的、重要的,其他形式的方程皆可由它推导.直线方程的特殊形式都具有明显的几何意义,但又都有一些特定的限制条件,应用时要注意它们各自适用的范围,以避免漏解.常需要分类讨论.
[例1]已知△ABC的三个顶点是A(4,-1)、B(0,3)、C(7,3),
(1)求AB边的中线所在直线的方程;
(2)求∠C的一平分线的方程.
解(1)由中点公式得AB中点D(2,1),中线CD所在直线的方程为
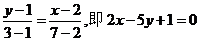 .
.
(2)由两点间距离公式得|AC|=5, |BC|=7.
设∠C的平分线与边AB的交点为E,由三角形内角平分线的性质知E分有向线段AB所成的比λ=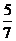 ,由定比分点公式得
,由定比分点公式得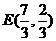 ,
,
由两点式方程得,直线CE的方程为:x-2y-1=0.
∴∠C的平分线的方程为:x-2y-1=0 (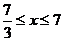 ).
).
[例2] 已知两点A(-1,2)、B(m,3)
(1)求直线AB的斜率k与倾斜角α;
(2)求直线AB的方程;
(3)已知实数m∈[-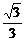 -1,
-1,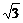 -1],求直线AB的倾斜角α的取值范围.
-1],求直线AB的倾斜角α的取值范围.
解:(1)当m=-1时,直线AB的斜率不存在,倾斜角α= .
.
当m≠-1时,k=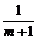 ,
,
当m>-1时,α=arctan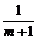 ,
,
当m<-1时,α=π+arctan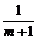 .
.
(2)当m=-1时,AB:x=-1,
当m≠1时,AB:y-2=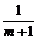 (x+1).
(x+1).
(3)①当m=-1时,α= ;
;
②当m≠-1时,
∵k=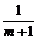 ∈(-∞,-
∈(-∞,-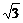 ]∪[
]∪[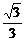 ,+∞),
,+∞),
∴α∈[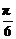 ,
, )∪(
)∪( ,
,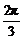 ]
]
故综合①、②得,直线AB的倾斜角α∈[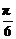 ,
,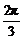 ]
]
[例3]已知两直线a1x+b1y+1=0和a2x+b2y+1=0的交点为P(2,3),求过两点Q1(a1,b1)、Q2(a2,b2)(a1≠a2)的直线方程
分析:利用点斜式或直线与方程的概念进行解答
解:∵P(2,3)在已知直线上,
∴ 2a1+3b1+1=0,2a2+3b2+1=0
∴2(a1-a2)+3(b1-b2)=0,即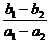 =-
=-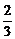
∴所求直线方程为y-b1=-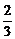 (x-a1)
(x-a1)
∴2x+3y-(2a1+3b1)=0,即2x+3y+1=0
◆提炼方法:1.由已知求斜率; 2.运用了整体代入的思想,方法巧妙.
[例4]一条直线经过点P(3,2),并且分别满足下列条件,求直线方程:
(1)倾斜角是直线x-4y+3=0的倾斜角的2倍;
(2)与x、y轴的正半轴交于A、B两点,且△AOB的面积最小(O为坐标原点)
解:(1)设所求直线倾斜角为θ,已知直线的倾斜角为α,则θ=2α,且tanα=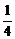 ,tanθ=tan2α=
,tanθ=tan2α=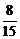 ,
,
从而方程为8x-15y+6=0
(2)设直线方程为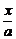 +
+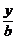 =1,a>0,b>0,
=1,a>0,b>0,
代入P(3,2),得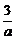 +
+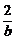 =1≥2
=1≥2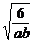 ,得ab≥24,
,得ab≥24,
从而S△AOB=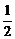 ab≥12,
ab≥12,
此时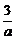 =
=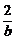 ,∴k=-
,∴k=- =-
=-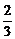
∴方程为2x+3y-12=0
◆解法点评:此题(2)也可以转化成关于a或b的一元函数后再求其最小值
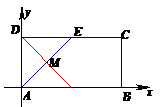
[研讨.欣赏](2005广东) 在平面直角坐标系中,已知矩形ABCD的长为2,宽为1,AB、AD边分别在x轴、y轴的正半轴上,A点与坐标原点重合(如图5所示).将矩形折叠,使A点落在线段DC上.
在平面直角坐标系中,已知矩形ABCD的长为2,宽为1,AB、AD边分别在x轴、y轴的正半轴上,A点与坐标原点重合(如图5所示).将矩形折叠,使A点落在线段DC上.
(Ⅰ)若折痕所在直线的斜率为k,试写出折痕所在直线的方程;
(Ⅱ)求折痕的长的最大值.
解:设点A关于拆痕的对称点E,由于点E在线段DC上,故可设点E的坐标为(t,1)(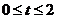 ).
).
(图3) (图4)
(图5) (图6)
(Ⅰ)若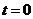 ,则“拆痕”所在的直线为线段AD的中垂线,它的方程为
,则“拆痕”所在的直线为线段AD的中垂线,它的方程为  ;
;
若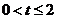 ,由
,由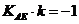 ,则
,则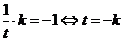 ,
,
从而线段AE的中点M的坐标为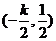 ,故“拆痕”所在直线的方程为
,故“拆痕”所在直线的方程为 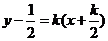 .
.
综上所述,“拆痕”所在直线的方程为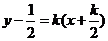 .
.
(Ⅱ)设“拆痕”的长为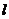 .
.
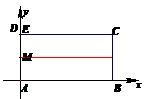
(1)当“折痕”过AD的中点时(如图3), ;
;
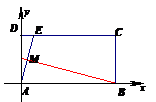
当“折痕”过点B时(如图4),由于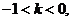 求得
求得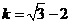 .所以,当
.所以,当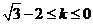 时,“折痕”与y轴及
时,“折痕”与y轴及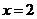 均有交点,分别求得为
均有交点,分别求得为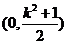 、
、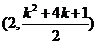 .
.
此时, 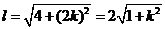 .
.
由于l是关于k的函数,它在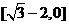 上是减函数,所以,当
上是减函数,所以,当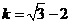 时,
时,
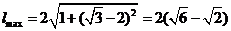 .
.
(2)当“折痕”过点D时(如图5),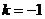 .所以,当
.所以,当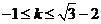 时,“折痕”与y轴及
时,“折痕”与y轴及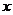 轴均有交点,分别求得为
轴均有交点,分别求得为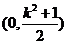 、
、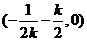 .
.
此时, 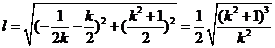 .
.
设 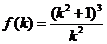 ,则
,则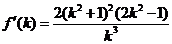 ,由此得:
,由此得:
当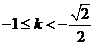 时,
时,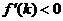 ;当
;当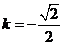 时,
时,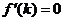 ;当
;当 时,
时,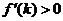 .所以,
.所以,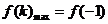 ,或
,或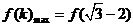 .
.
由于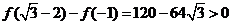 ,所以,
,所以,
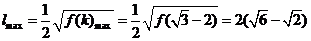 .
.
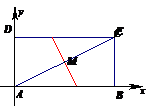
(3)当“折痕”过AC的中点时(如图6),求得 .所以,当
.所以,当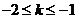 时,“折痕”与
时,“折痕”与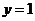 及
及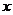 轴均有交点,分别求得为
轴均有交点,分别求得为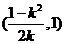 、
、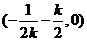 .
.
此时, 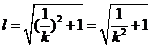 .
.
由于l是关于k的函数,它在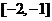 上是增函数,所以,当
上是增函数,所以,当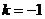 时,
时,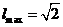 .
.
由于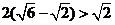 ,所以“拆痕”的长的最大值为
,所以“拆痕”的长的最大值为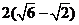 .
.
6.解析:由方向向量定义即得a1为(2,1)或(1,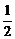 ).
).
a1·a2=0,即a1⊥a2.
也就是l1⊥l2,即k1·k2=-1.
再由点斜式可得l2的方程为2x+y-3=0.
答案:(2,1)或(1,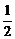 ) 2x+y-3=0
) 2x+y-3=0
4.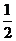 ; 5.(x+y=3或y=x/2)强调:截距式的使用范围
; 5.(x+y=3或y=x/2)强调:截距式的使用范围
3.解析:对命题①④,方程不能表示倾斜角是90°的直线,对命题③,当直线平行于一条坐标轴时,则直线在该坐标轴上截距不存在,故不能用截距式表示直线,只有②正确。
6.(2005北京东城检测)已知直线l1:x-2y+3=0,那么直线l1的方向向量a1为____________(注:只需写出一个正确答案即可);l2过点(1,1),l2的方向向量a2,且a1·a2=0,则l2的方程为____________.
简答:1-3.DBB;
5.过点A(2,1),且在x,y轴上截距相等的直线方程是
4.(2006北京11)若三点 共线,则
共线,则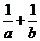 的值等于______.
的值等于______.
3.下列四个命题:①经过定点P0(x0,y0)的直线都可以用方程y-y0=k(x-x0)表示;②经过任意两个不同的点P1(x1,y1)、P2(x2,y2)的直线都可以用方程(x2-x1)(x-x1)=(y2-y1)(y-y1)表示;③不经过原点的直线都可以用方程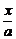 +
+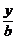 =1表示;④经过定点A(0,b)的直线都可以用方程y=kx+b表示其中真命题的个数是
=1表示;④经过定点A(0,b)的直线都可以用方程y=kx+b表示其中真命题的个数是
A.0 B.1 C.2 D.3
1.直线xtan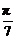 +y=0的倾斜角是
+y=0的倾斜角是
A.-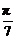 B.
B.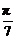 C.
C.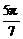 D.
D.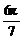
2直线xcosα+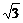 y+2=0的倾斜角范围是
y+2=0的倾斜角范围是
A[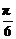 ,
, )∪(
)∪( ,
,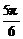 ] B[0,
] B[0,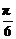 ]∪[
]∪[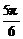 ,π)
,π)
C[0,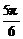 ]
D[
]
D[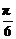 ,
,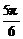 ]
]
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com