
5.气体摩尔体积
⑴概念: 。
⑵符号:
⑶单位: 。
⑷标准状况下的气体摩尔体积
①标准状况是指: 温度 ℃,压强 Pa。
②标准状况下的气体摩尔体积是: 。
⑸影响物质体积大小的因素:
①
②
③
4.摩尔质量
⑴概念: 。
⑵符号: ⑶单位: 。
⑷注意点:与相对分子质量、式量和1mol物质的质量的异同:含义上 同,数值上 同。
3.阿伏加德罗常数
⑴含义: 。
⑵符号: ⑶单位: 。
⑷注意点:
①阿伏加德罗常数的基准是12g 中的原子个数。
②现阶段常取 为阿伏加德罗常数的近似值。
2.摩尔
⑴概念: 。
⑵符号: ⑶基准 。
⑷注意点:
①当描述物质的物质的量(使用摩尔)时,必须指明物质微粒的 。
②常见的微观粒子有: 或它们特定的组合。
1.物质的量
⑴概念: 。
⑵符号: ⑶单位: 。
10. 某房地产公司要在荒地ABCDE(如下图)上划出一块长方形地面(不改变方位)建造一幢八层的公寓楼,问如何设计才能使公寓占地面积最大?并求出最大面积.(精确到1 m2)

解:如下图,在线段AB上任取一点P,
分别向CD、DE作垂线划得一块长方形土地,建立如下图所示的直角坐标系,则AB的方程为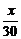 +
+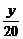 =1.设P(x,20-
=1.设P(x,20-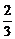 x),则长方形面积S=(100-x)[80-(20-
x),则长方形面积S=(100-x)[80-(20-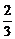 x)]
(0≤x≤30).
x)]
(0≤x≤30).

化简得S=-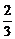 x2+
x2+ x+6000(0≤x≤30).
x+6000(0≤x≤30).
配方,易得x=5,y=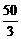 时,S最大,其最大值为6017 m2.
时,S最大,其最大值为6017 m2.
[探索题](2005天津)
某人在一山坡P处观看对面山项上的一座铁塔,如图所示,塔高BC=80(米),塔所在的山高OB=220(米),OA=200(米),图中所示的山坡可视为直线l且点P在直线l上,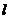 与水平地面的夹角为
与水平地面的夹角为 ,
,  试问此人距水平地面多高时,观看塔的视角∠BPC最大(不计此人的身高)
试问此人距水平地面多高时,观看塔的视角∠BPC最大(不计此人的身高)

解:如图所示,建立平面直角坐标系,
则A(200,0),B(0,220),C(0,300),
直线l的方程为 设点P的坐标为(x,y),
设点P的坐标为(x,y),
则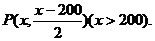
由经过两点的直线的斜率公式 

由直线PC到直线PB的角的公式得


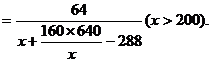
要使tanBPC达到最大,只须 达到最小,由均值不等式
达到最小,由均值不等式
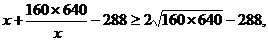
当且仅当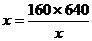 时上式取得等号,故当x=320时tanBPC最大,这时,点P的纵坐标y为
时上式取得等号,故当x=320时tanBPC最大,这时,点P的纵坐标y为

由此实际问题知, 所以tanBPC最大时,∠BPC最大,故当此人距水平地面60米高时,观看铁塔的视角∠BPC最大.
所以tanBPC最大时,∠BPC最大,故当此人距水平地面60米高时,观看铁塔的视角∠BPC最大.
9. 在直线方程y=kx+b中,当x∈[-3,4]时,y∈[-8,13],求此直线方程.
解:当x的区间的左端点与y的区间的左端点对应,x的区间的右端点与y的区间的右端点对应时,得

∴直线方程为y=3x+1.
当x的区间的左端点与y的区间的右端点对应,x的区间右端点与y的区间的左端点对应时,得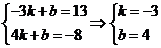
∴所求的直线方程为y=-3x+4或y=3x+1.
8.过点P(2,1)作直线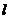 分别交x,y轴正并轴于A,B两点
分别交x,y轴正并轴于A,B两点
(1)当ΔAOB面积最小时,求直线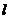 的方程;
的方程;
(2)当|PA|´|PB|取最小值时,求直线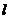 的方程
的方程
解:(1)设所求的直线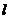 方程为
方程为 (a>0,b>0),
(a>0,b>0),
由已知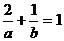

于是 =
=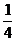 ,∴SΔ AOB=
,∴SΔ AOB= ³4,
³4,
当且仅当 ,即a=4,b=2时取等号,
,即a=4,b=2时取等号,
此时直线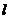 的方程为
的方程为 ,即x+2y─4=0
,即x+2y─4=0
(2):设直线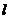 :y─1=k(x─2),分别令y=0,x=0,得A(2─
:y─1=k(x─2),分别令y=0,x=0,得A(2─ ,0), B(0,1─2k)
,0), B(0,1─2k)
则|PA|´|PB|= =
=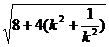 ³4,当且仅当k2=1,即k=±1时,取最小值, 又k<0,
³4,当且仅当k2=1,即k=±1时,取最小值, 又k<0,
∴k=─1, 此时直线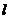 的方程为x+y─3=0
的方程为x+y─3=0
7.已知两点A(-1,2)、B(m,3)
(1)求直线AB的斜率k与倾斜角α;
(2)求直线AB的方程;
(3)已知实数m∈[-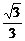 -1,
-1,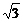 -1],求直线AB的倾斜角α的取值范围.
-1],求直线AB的倾斜角α的取值范围.
解:(1)当m=-1时,直线AB的斜率不存在,倾斜角α=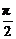 .
.
当m≠-1时,k=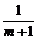 ,
,
当m>-1时,α=arctan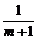 ,
,
当m<-1时,α=π+arctan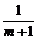 .
.
(2)当m=-1时,AB:x=-1,
当m≠1时,AB:y-2=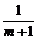 (x+1).
(x+1).
(3)①当m=-1时,α=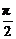 ;
;
②当m≠-1时,
∵k=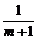 ∈(-∞,-
∈(-∞,-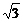 ]∪[
]∪[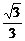 ,+∞),
,+∞),
∴α∈[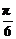 ,
,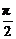 )∪(
)∪(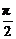 ,
,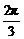 ]
]
故综合①、②得,直线AB的倾斜角α∈[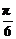 ,
,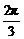 ]
]
6.解:由于将直线平移不影响其斜率的值,故可设点O(0,0)在直线上,则依题意O点经平移后的坐标为P(─3,1), 故直线l过两点P,O,求出斜率即可
[解答题]
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com