
4、农村地区人口过度增长带来的过度开垦,进而森林草场破坏、水土流失、土地沙化、河湖淤塞等相关的生态问题。以及农村年轻劳力外出打工造成的劳力短缺问题。
农村剩余劳力大量拥入城市(即城市化过程),民工的盲目流动带来的交通紧张、社会治安变差,住房紧张及其它社会问题。
3、与人口结构有关的问题及解决办法。如人口的年龄结构、性别结构、学历结构、就业结构、城乡结构等,与现实密切相关的就业结构,与人口增长相关的是年龄结构,与未来发展相关的是学历结构。
2、归因于人口零及负增长带来的人口老龄化问题,包括老龄化的形成机制,对社会福利制度的影响,劳力的短缺,社会伦理观念的转化,以及政府相应的政策等。其中以西欧,北欧,北美诸国表现比较突出。
人口问题是当今世界面临的难题之一。它既包括由于人口过度增长带来的教育普及、就业因难、住房紧张、社会保险不足、人均收入和健康状况下降的困难(主要表现在亚、非、拉三大洲发展中国家);也包括由于人口零增长或负增长带来的劳动力不足、老龄人口福利水平下降的新难题(主要表现在欧美的发达国家);同时还包括由于人口分布的经济发展和经济发展不平衡造成的人口迁移。站在全球的角度来讲,人口的过度增长是所有人口问题的根源之一。由于地球的人口负担过重,世界出现了相应的耕地、粮食、能源不足,环境污染严重等现实问题。树立正确的人口观及其人均意识是中学地理教学的主要任务之一,因为地理学研究的重点就是人地关系。历年高考地理试题都重视考生对人口问题的观点和知识考查,主要的考查方式与内容有:
1、归因于人口过度增长带来的人均耕地、人均资源、人均粮食、人均能源、人均国民生产总值及人均收入,人均住房面积等不断下降的形成机制,地区差异及解决措施等。其中以中国和印度等亚、非、拉发展中国家表现最为突出。
22. 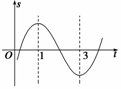 解
解  =3t2+2bt+c.
=3t2+2bt+c.
由图象可知,s(t)在t=1和t=3处取得极值.
则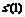 =0,
=0, 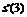 =0.
=0.
即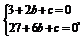 解得
解得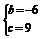
∴ =3t2-12t+9=3(t-1)(t-3).
=3t2-12t+9=3(t-1)(t-3).
当t∈[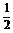 ,1)时,
,1)时, >0.
>0.
当t∈(1,3)时, <0.
<0.
当t∈(3,4)时, >0.
>0.
则当t=1时,s(t)取得极大值为4+d.
又s(4)=4+d,
故t∈[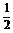 ,4]时,s(t)的最大值为4+d.
,4]时,s(t)的最大值为4+d.
已知s(t)<3d2在[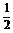 ,4]上恒成立,
,4]上恒成立,
∴s(t)max<3d2.即4+d<3d2.
解得d>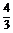 或d<-1.∴d的取值范围是{d|d>
或d<-1.∴d的取值范围是{d|d>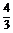 或d<-1}.
或d<-1}.
21. 解 设P(x0,y0),则y0= ,
,
∴过点P的切线斜率k=x0,
当x0=0时不合题意,∴x0≠0.
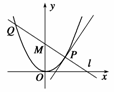 ∴直线l的斜率kl=-
∴直线l的斜率kl=-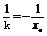 ,
,
∴直线l的方程为y-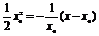 .
.
此式与y=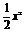 联立消去y得
联立消去y得
x2+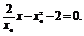
设Q(x1,y1),M(x,y).∵M是PQ的中点,
∴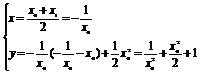
消去x0,得y=x2+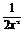 +1 (x≠0)就是所求的轨迹方程.由x≠0知x2>0,
+1 (x≠0)就是所求的轨迹方程.由x≠0知x2>0,
∴y=x2+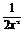 +1≥2
+1≥2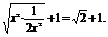
上式等号仅当x2=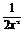 ,即x=±
,即x=±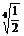 时成立,
时成立,
所以点M到x轴的最短距离是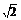 +1.
+1.
20.解 (1)∵函数F(x)=f(x)-3x2是奇函数,
∴F(-x)=-F(x),化简计算得b=3.
∵函数f(x)在x=-1处取极值,∴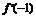 =0.
=0.
f(x)=-2x3+3x2+cx,
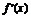 =-6x2+6x+c
=-6x2+6x+c
∴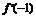 =-6-6+c=0,c=12.
=-6-6+c=0,c=12.
∴f(x)=-2x3+3x2+12x,
(2)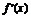 =-6x2+6x+12=-6(x2-x-2).
=-6x2+6x+12=-6(x2-x-2).
令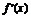 =0,得x1=-1,x2=2,
=0,得x1=-1,x2=2,
|
x |
-3 |
(-3,-1) |
-1 |
(-1,2) |
2 |
(2,3) |
3 |
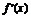 |
|
- |
0 |
+ |
0 |
- |
|
|
f(x) |
45 |
↘ |
-7 |
↗ |
20 |
↘ |
9 |
∴函数f(x)在[-3,-1]和[2,3]上是减函数,
函数f(x)在[-1,2]上是增函数.
19.解 f(x)=x(x-1)(x-a)=x3-(a+1)x2+ax
∴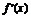 =3x2-2(a+1)x+a
=3x2-2(a+1)x+a
要使函数f(x)=x(x-1)(x-a)在(2,+∞)上是增函数,只需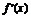 =3x2-2(a+1)x+a在(2,+∞)上满足
=3x2-2(a+1)x+a在(2,+∞)上满足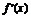 ≥0即可. ∵
≥0即可. ∵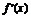 =3x2-2(a+1)x+a的对称轴是x=
=3x2-2(a+1)x+a的对称轴是x=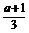 ,
,
∴a的取值应满足: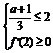 或
或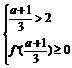
解得:a≤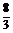 .∴a的取值范围是a≤
.∴a的取值范围是a≤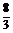 .
.
18.解 命题p:由原式得f(x)=x3-ax2-4x+4a,
∴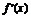 =3x2-2ax-4,y′的图象为开口向上且过点(0,-4)的抛物线.
=3x2-2ax-4,y′的图象为开口向上且过点(0,-4)的抛物线.
由条件得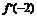 ≥0且
≥0且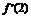 ≥0,
≥0,
即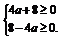 ∴-2≤a≤2.
∴-2≤a≤2.
命题q: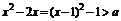
∵该不等式的解集为R,∴a<-1.
当p正确q不正确时,-1≤a≤2;
当p不正确q正确时,a<-2.
∴a的取值范围是(-∞,-2)∪[-1,2].
17.解 (1)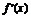 =3x2-x+b,因f(x)在(-∞,+∞)上是增函数,则
=3x2-x+b,因f(x)在(-∞,+∞)上是增函数,则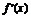 ≥0.即3x2-x+b≥0,
≥0.即3x2-x+b≥0,
∴b≥x-3x2在(-∞,+∞)恒成立.设g(x)=x-3x2.
当x=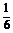 时,g(x)max=
时,g(x)max=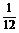 ,∴b≥
,∴b≥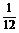 .
.
(2)由题意知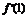 =0,即3-1+b=0,∴b=-2.
=0,即3-1+b=0,∴b=-2.
x∈[-1,2]时,f(x)<c2恒成立,只需f(x)在[-1,2]上的最大值小于c2即可.因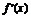 =3x2-x-2,令
=3x2-x-2,令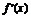 =0,得x=1或x=-
=0,得x=1或x=-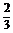 .∵f(1)=-
.∵f(1)=- +c,
+c,
f(-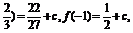 f(2)=2+c.
f(2)=2+c.
∴f(x)max=f(2)=2+c,∴2+c<c2.解得c>2或c<-1,所以c的取值范围为(-∞,-1)∪(2,+∞).
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com