253. 　如图所示，正三棱锥S-ABC的侧棱与底面的边长相等，如果E、F分别为SC、AB的中点，求异面直线EF与SA所成的角.

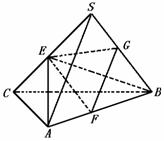
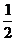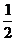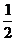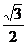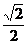解析：计算EF、SA所成的角，可把SA平移，使其角的顶点在EF上.为此取SB之中点G，连GE、GF、BE、AE，由三角形中位线定理：GE＝BC，GF＝SA，且GF∥SA，所以∠GFE就是EF与SA所成的角.若设此正三棱锥棱长为a，那么GF＝GE＝a,EA＝EB＝a,EF＝＝a，因为ΔEGF为等腰直角三角形.∠EFG＝45°，所以EF与SA所成的角为45°.

说明　 异面直线所成角的求法：

利用定义构造角，可固定一条，平移另一条，或同时平移到某个特殊的位置，顶点选在特殊的位置上，通过证明所作的角就是所求的角或者补角，解三角形，可求.

252.　 如图，在棱长为a的正方体ABCD-A₁B₁C₁D₁中，异面直线AA₁和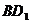的中点分别是E、F.

(1)证明EF是AA₁与BD₁的公垂线段；

(2)求异面直线AA₁和BD₁间的距离.

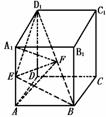
解析：(1)连接ED₁、EB，

则显然ED₁＝EB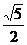＝a

又F为BD₁之中点.

∴　 EF⊥BD₁；

连接FA₁，FA.

∵　 F为正方体的中心，

∴　 FA＝FA₁，又E为AA₁之中点，

∴　 EF⊥A₁A.

故EF为AA₁与BD₁的公垂线段.

(2)在RtΔEFD₁中

EF＝＝.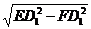

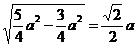故AA₁到BD₁间的距离是.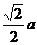

评析：今后学习了线面的位置关系之后，可以利用“转化”的思想求距离.

251.　 已知两平面α，β相交于直线a，直线b在β内与直线a相交于A点，直线c在平面α内与直线a平行，请用反证法论证b,c为异面直线.

解析：这题规定用反证法，提出与结论相反的假定后，要注意分可能的几种情况讨论.

证：用反证法.

假设b,c共面，则b∥c或b,c相交.

(1)若b∥c,∵　 c∥a,　 ∴　 a∥b这与b∩a＝A的已知条件矛盾；

(2)若b∩c＝P,∵　 bβ，∴　 P∈β.

又∵　 cα，∴　 P∈α.　 ∴　 P∈α∩β而α∩β＝a.

∴　 P∈a，这样c,a有了公共点P，这与a∥c的已知条件矛盾.

综上所述，假设不成立，所以b、c为异面直线.

说明　 本题如不指明用反证法，也可以考虑用平面直线的判定定理来证明.

14．下面是某同学的一篇演讲稿的开头段，请找出其中的语病加以修改。(4分)

每个时代的年轻人都有自己的精神偶像。在这些偶像身上，闪烁着时代精神的光芒。无论是他们的个性特征、事业成就，还是他们的生活情趣、奋斗经历，都令人们佩服敬慕、钦仰并将其作为自己的人生榜样，从而使他们成为在人生旅途中不断奋进的“永动机”。

修改：