
3.吸进人体内的O2有2%转化为氧化性极强的活性氧副产物,如·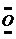 ·等,这些活性氧能加速人体衰老,被称为“夺命杀手”。我国科学家尝试用含硒化合物Na2SeO3消除人体内的活性氧,在消除活性氧时,Na2SeO3的作用是( )
·等,这些活性氧能加速人体衰老,被称为“夺命杀手”。我国科学家尝试用含硒化合物Na2SeO3消除人体内的活性氧,在消除活性氧时,Na2SeO3的作用是( )
A.还原剂 B.氧化剂
C.既是氧化剂,又是还原剂 D.以上均不是
2.氨与重水(D2O)形成的碱与盐酸反应,这一反应生成的盐中阳离子的化学式是
A.NH3D+ B.NH2D2+ C.ND3H+ D.NH4+
1.氮的固定是指: ( )
A.植物从土壤中吸收含氮养料;
B.豆科植物根瘤菌将含氮化合物转变为植物蛋白质;
C.将氨转变成硝酸及其它氮的化合物;
D.将空气中的氮气转变为含氮化合物。
260. .若a、b为异面直线,P为空间一点,过P且与a、b所成角均为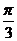 的直线有( )
的直线有( )
A.二条 B.二条或三条
C.二条或四条 D.二条、三条或四条
解析:D
259. 已知异面直线a与b所成的角为50°,P为空间一定点,则过点P且与a、b所成的角都是30°的直线有且仅有( )
A.1条 B.2条 C.3条 D.4条
解析: 过P点分别作直线a′∥a,b′∥b,则a′与b′的夹角为50°,由异面直线所成的角的定义可知,过P点与a′,b′成30°角的条数,就是所求的条数.
画图可知,过P点与a′、b′成30°角的直线只有两条.
∴ 应选B.
258. 在棱长为1的正方体ABCD-A1B1C1D1中,M和N分别为A1B1和BB1的中点,那么直线AM与CN所成角的余弦值是( )
A.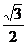 B.
B.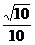 C.
C.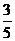 D.
D.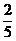

解析:由图所示,AM与CN是异面直线,过N作平行于AM的平行线NP,交AB于P,由定义可知∠PNC就是AM与CN所成的角.因ΔPBC,ΔPBN,ΔCBN皆为直角三角形,且BP=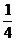 ,BN=
,BN=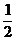 ,BC=1,故PN2=(
,BC=1,故PN2=(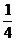 )2+(
)2+(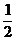 )2=
)2=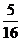 ,CN2=(
,CN2=(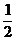 )2+12=
)2+12= ,PC2=(
,PC2=(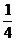 )2+12=
)2+12=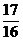 ,在ΔPCN中cos∠PNC=
,在ΔPCN中cos∠PNC= ,所以cos∠PNC=
,所以cos∠PNC=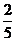 ,因此应选D.
,因此应选D.
257. 如图,ABCD-A1B1C1D1是正方体,B1E1=D1F1= ,则BE1与DF1所成角的余弦值是( )
,则BE1与DF1所成角的余弦值是( )
A. B.
B.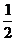 C.
C.
 D.
D.
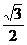
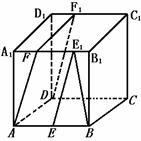
解析:过A点在平面ABB1A1内作AF,使A1F=D1F1,则ADF1F是平行四边形,∴FA∥DF1,再过E1在平面ABB1A1内作E1E∥FA,则∠BE1E即是BE1与DF1所成的角,由已知BE1=DF1= ,ABCD-A1B1C1D1是正方体,∴ E1E=
,ABCD-A1B1C1D1是正方体,∴ E1E=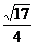 A1B1,
A1B1,
又DF1=AF=E1E,DF1=BE1.
∴
E1E=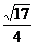 A1B1,EB=
A1B1,EB=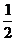 A1B1
A1B1
在ΔBE1E中,cos∠BE1E=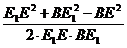 =
= .
.
∴ 应选A.
256.分别和两条异面直线AB、CD同时相交的两条直线AC、BD一定是异面直线,为什么?
证明:假设AC、BD不异面,则它们都在某个平面α内,这时A、B、C、D四点都在α上,由公理1知A、B、C、D α,这与已知AB与CD异面矛盾,所以AC、BD一定是异面直线.
α,这与已知AB与CD异面矛盾,所以AC、BD一定是异面直线.
255.已知:直线a和直线b是异面直线,直线c∥a,直线b与c不相交,求证:b、c是异面直线.
证:因为b,c不相交,b、c的位置关系有b∥c或b、c异面两种可能.
假设b∥c,∵ c∥a,∴ a∥b,这与已知a,b是异面直线矛盾.
所以b与c不能平行,又b、c不相交
所以b,c是异面直线.
254. 在空间四边形ABCD中,M、N、P、Q分别是四边上的点,且满足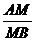 =
=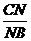 =
=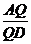 =
=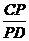 =k.
=k.
(1)求证:M、N、P、Q共面.
(2)当对角线AC=a,BD=b,且MNPQ是正方形时,求AC、BD所成的角及k的值(用a,b表示)
解析:(1)∵ 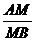 =
=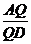 =k
=k
∴
MQ∥BD,且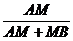 =
=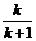
∴
 =
=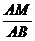 =
=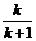
∴
MQ=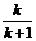 BD
BD
又
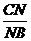 =
=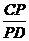 =k
=k
∴
PN∥BD,且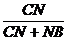 =
=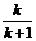
∴
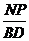 =
=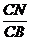 =
=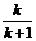 从而NP=
从而NP=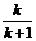 BD
BD
∴ MQ∥NP,MQ,NP共面,从而M、N、P、Q四点共面.
(2)∵ 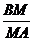 =
=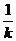 ,
,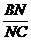 =
=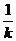
∴
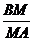 =
=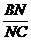 =
=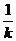 ,
,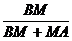 =
=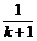
∴ MN∥AC,又NP∥BD.
∴ MN与NP所成的角等于AC与BD所成的角.
∵ MNPQ是正方形,∴ ∠MNP=90°
∴ AC与BD所成的角为90°,
又AC=a,BD=b,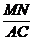 =
=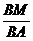 =
=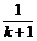
∴
MN=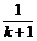 a
a
又
MQ=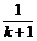 b,且MQ=MN,
b,且MQ=MN,
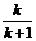 b=
b=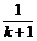 a,即k=
a,即k=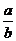 .
.
说明:公理4是证明空间两直线平行的基本出发点.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com