
15、(12分)如图所示,质量为m的物体放在半径为 1m的光滑半圆槽内,当小球和半圆槽一起以a=7.5m/s2的加速度在水平地面向右加速度时,求小球离圆槽底的高度(g=10m/s2).
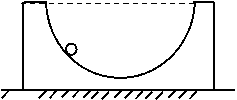 ·
·

14、(12分)如图所示,物体的质量为m=4kg,与水平地面间的动摩擦因数为0.2,在倾角为370,F=10N的恒力作用下,由静止开始运动,当t=5s时撤去F,求(1)物体做加速运动时的加速度;(2)物体一共运动了多远。(g=10m/s2)
 F
F
 370
370


13、(10分)在火车站台上有一观察者,在列车
开动时恰好站在第一节车厢的最前端,列车起动
后做匀加速运动,经过4s第一节车厢通过观察者,
整个列车通过他的时间为20s,设每节车厢等长,
车厢连接处长度不计,求:(1)这列列车共有多少节车厢;(2)最后9节车厢通过观察者所经历的时间。
12、(10分)
(1)请在右边坐标系中画图:
(2)__________________________。
(3)__________________________。
(4)__________________________。
11、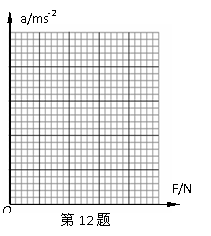 (9分)_______________; _____________________;_____________________。
(9分)_______________; _____________________;_____________________。
12、(10分)某同学在“探究加速度与力,加速度与质量关系”的实验中,测得加速度a与拉力F的数据如下表所示:
|
F(N) |
0.20 |
0.30 |
0.40 |
0.50 |
0.60 |
|
a(m/s2) |
0.11 |
0.19 |
0.29 |
0.40 |
0.51 |
(1)根据表格中的数据在坐标图上作出a-F图像;(2)图像斜率的物理意义是__________。
(3)图像(或延长线)与F轴的截距的物理意义是________________。
(4)小车和砝码的总质量为_________kg
第Ⅱ卷:非选择题部分(共82分)
11、(9分)某同学利用打点计时器所记录的纸带,来研究做匀变速直线运动小车的运动情况,实验中获得一条纸带,如图所示,各计数点中间还有4个点没有画出来,已知所用电源的频率为50HZ,测得x1=3.18cm,x2=6.75cm,x3=10.70cm,x4=15.05cm,,则在打B点时小车的速度为VB=_____________;小车运动的加速度表达式为a=_______________;代入数据后算出加速度大小为___________________。(计算结果保留三位有效数字)。

O A B C D




 · ·
·
·
·
· ·
·
·
·
 x1
x1
 x2
x2

x3

x4
20、(本大题满分16分)
解:(1)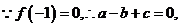

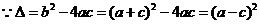 当
当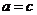 时
时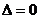 ,
,
函数 有一个零点;当
有一个零点;当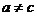 时,
时,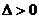 ,函数
,函数 有两个零点。………4分
有两个零点。………4分
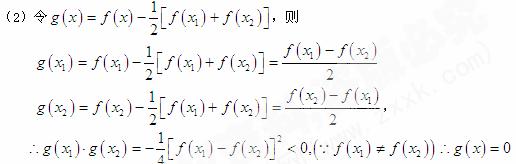
在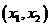 内必有一个实根。即
内必有一个实根。即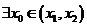 ,使
,使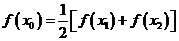 成立。
成立。
………………10分
(3)假设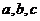 存在,由①知抛物线的对称轴为x=-1,且
存在,由①知抛物线的对称轴为x=-1,且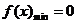
∴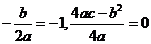
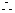
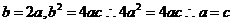
由②知对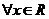 ,都有
,都有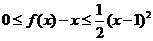
令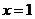 得
得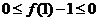
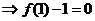
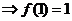
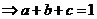 ……………13分
……………13分
由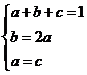 得
得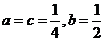 , ………………………………………………15分
, ………………………………………………15分
当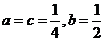 时,
时,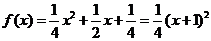 ,其顶点为(-1,0)满足条件①,又
,其顶点为(-1,0)满足条件①,又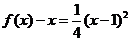
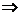 对
对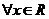 ,都有
,都有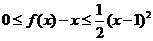 ,满足条件②。∴存在
,满足条件②。∴存在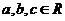 ,使
,使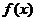 同时满足条件①、②。…………………………16分
同时满足条件①、②。…………………………16分
19、(本大题满分16分)
(Ⅰ)∵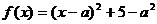 (
(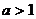 ),∴
),∴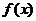 在
在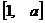 上是减函数,
上是减函数,
又定义域和值域均为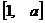 ,∴
,∴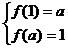 , 即
, 即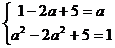 ,
解得
,
解得 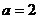 .
.
(II) ∵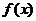 在区间
在区间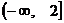 上是减函数,∴
上是减函数,∴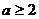 ,
,
又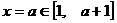 ,且,
,且,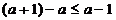
∴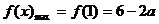 ,
,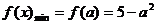 .
.
∵对任意的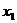 ,
,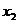
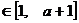 ,总有
,总有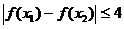 ,
,
∴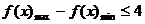 ,
,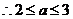 .
.
18、(本大题满分16分)
解:(1)由题意,得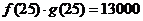 ,即
,即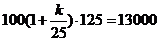 ,解得
,解得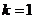 ……3分
……3分
(2)
=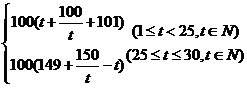
(3)①当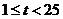 时,因为
时,因为 ,所以当
,所以当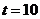 时,
时,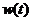 有最小值12100
有最小值12100
②当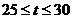 时,∵
时,∵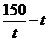 在
在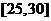 上递减,∴当
上递减,∴当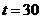 时,
时,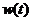 有最小值12400
有最小值12400
∵12100〈12400,∴当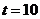 时,该商品的日销售金额
时,该商品的日销售金额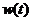 取得最小值为12100
取得最小值为12100
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com