

3.由完全相同的两只灵敏电流表改装成的量程不同的电流表并联起来接入同一条电路测量电流强度,两表皆正常工作,下列说法正确的是( )
A.两表指针偏角相同,读数一样
B.两表指针偏角、读数都不同
C.两表指针偏角相同,读数不一样
D.两表指针偏角不同,读数一样
解析:改装成的两电流表并联起来接入电路,两表头上的电压相同,内阻相同,所以流过表头的电流相同,指针偏角也相同.但由于两电流表的量程不同,读数一定不同.
答案:C
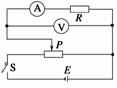
图20
2.将一块内阻为600 Ω、满偏电流为50 μA的电流表G改装成量程为0.6 A的电流表,应该( )
A.串联一个7.2×106 Ω的电阻
B.并联一个7.2×106 Ω的电阻
C.串联一个0.05 Ω的电阻
D.并联一个0.05 Ω的电阻
解析:将电流表的量程扩大,应并联电阻
由IgRg=(I-Ig)R得
R== Ω≈0.05 Ω.
答案:D
1.如图19所示,用一个量程为15 V的电压表,串联一只3.0 kΩ的固定电阻后,
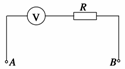
图19
再去测量一个电压为20 V的电路两端电压,表的示数恰为15 V,则此电压表的内阻RV( )
A.3 kΩ B.6 kΩ
C.9 kΩ D.12 kΩ
解析:电压表内阻RV上分压15 V,R上分压5 V,所以RV=3R=9 kΩ.
答案:C
21.(本小题满分14分) 已知椭圆E的中心在坐标原点,焦点在x轴上,离心率为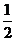 ,且椭圆E上一点到两个焦点距离之和为4;
,且椭圆E上一点到两个焦点距离之和为4;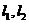 是过点P(0,2)且互相垂直的两条直线,
是过点P(0,2)且互相垂直的两条直线,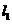 交E于A,B两点,
交E于A,B两点,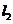 交E交C,D两点,AB,CD的中点分别为M,N。
交E交C,D两点,AB,CD的中点分别为M,N。
(Ⅰ)求椭圆E的方程;
(Ⅱ)求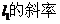 k的取值范围;
k的取值范围;
(Ⅲ)求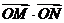 的取值范围。
的取值范围。
解:(Ⅰ)设椭圆方程为 ,由
,由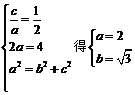
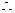 椭圆方程为
椭圆方程为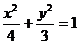
(2)由题意知,直线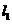 的斜率存在且不为零
的斜率存在且不为零 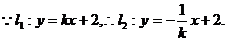
由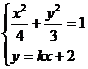 消去
消去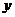 并化简整理,得
并化简整理,得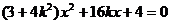
根据题意, ,解得
,解得
同理得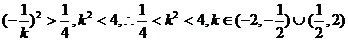
(Ⅲ)设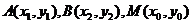 那么
那么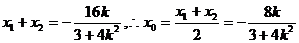
 同理得
同理得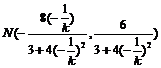 ,即
,即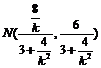

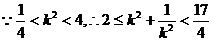
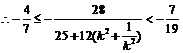
即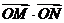 的取值范围是
的取值范围是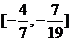
20.(本小题满分13分)已知函数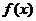 的定义域为[0,1]且同时满足:①对任意
的定义域为[0,1]且同时满足:①对任意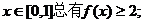 ②
②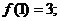 ③若
③若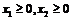 且
且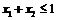 ,则有
,则有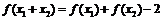
(I)求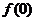 的值; (II)求
的值; (II)求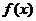 的最大值;
的最大值;
(III)设数列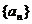 的前n项和为Sn,且
的前n项和为Sn,且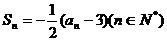 ,求
,求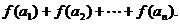
解:(Ⅰ)令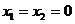 ,由③知
,由③知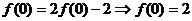
(Ⅱ)任取 ,则
,则
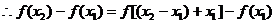
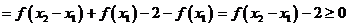
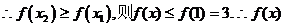 的最大值为3。
的最大值为3。
(Ⅲ)由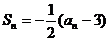 知,
知,
当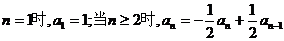
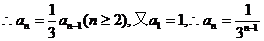
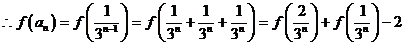
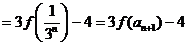
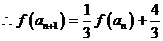
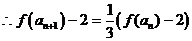
又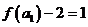
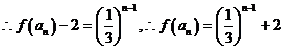
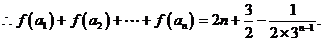
19.(本小题满分12分)已知数列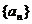 满足
满足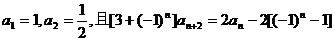
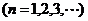
(1)求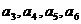 的值及数列
的值及数列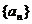 的通项公式;
的通项公式;
(2)令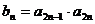 ,记数列
,记数列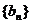 的前
的前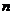 项和为
项和为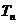 ,求证
,求证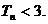
解:(1)分别令 可求得:
可求得:
当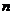 为奇数时,不妨设
为奇数时,不妨设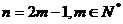 ,则
,则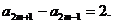
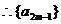 为等差数列,
为等差数列,
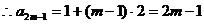 即
即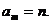
当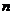 为偶数时,设
为偶数时,设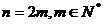 ,则
,则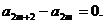
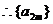 为等比数列,
为等比数列,
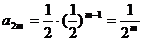 ,故
,故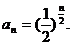
综上所述,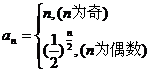
(2)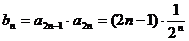
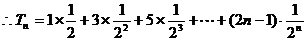
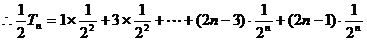 ,
,
两式相减: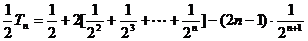
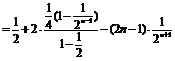
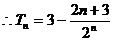 ,故
,故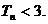
18. (本小题满分12分)已知二次函数
(本小题满分12分)已知二次函数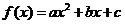 (
(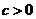 )的导函数的图象如图所示:
)的导函数的图象如图所示:
(Ⅰ)求函数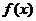 的解析式;
的解析式;
(Ⅱ)令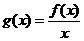 ,求
,求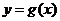 在
在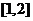 上的最大值.
上的最大值.
解析:(Ⅰ)因为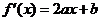 ,由图可知,
,由图可知,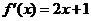 ,
,
∴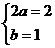 ,得
,得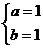 ,故所求函数解析式为
,故所求函数解析式为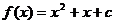 .
.
(Ⅱ)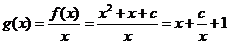 ,
,
则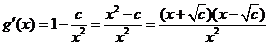 .
.
法一:①若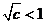 ,即
,即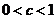 时,
时, ,
,
∴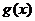 在
在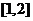 上是增函数,故
上是增函数,故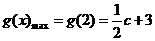 .
.
②若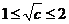 ,即
,即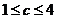 ,当
,当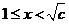 时,
时,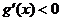 ;当
;当 时,
时, ;
;
∵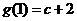 ,
,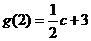 ,
,
∴当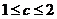 时,
时,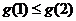 ,
,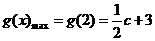 ;
;
当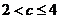 时,
时,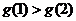 ,
,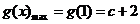 .
.
③若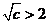 ,即
,即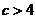 时,
时,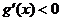 ,
,
∴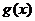 在
在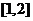 上是减函数,故
上是减函数,故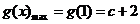 .
.
综上所述,当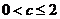 时,
时,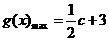 ;当
;当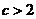 时,
时,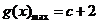 .
.
法二: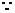 当
当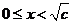 时,
时,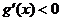 ;当
;当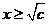 时,
时, ;
;
∴当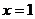 或
或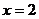 时,
时,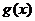 取得最大值,其中
取得最大值,其中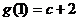 ,
,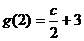 ,
,
当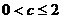 时,
时,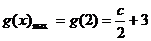 ;当
;当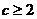 时,
时,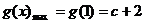 .
.
17.(本小题满分12分)在锐角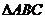 中 ,三个内角A、B、C的对边分别为a、b、c,且满足
中 ,三个内角A、B、C的对边分别为a、b、c,且满足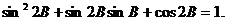
(1)求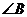 的值;
的值;
(2)若b=3,求a+c的最大值。
解:(1)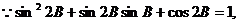
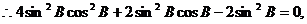
即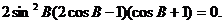
又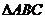 为锐角三角形,
为锐角三角形,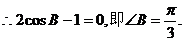
(2)由(1)知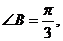
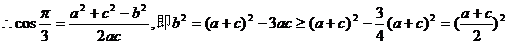
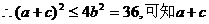 的最大值为6。
的最大值为6。
16.(本小题满分12分)已知锐角三角形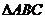 内角A、B、C对应边分别为a,b,c。
内角A、B、C对应边分别为a,b,c。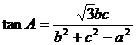
(Ⅰ)求A的大小; (Ⅱ)求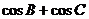 的取值范围。
的取值范围。
解:(Ⅰ)由余弦定理知,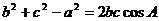 ∴
∴
∵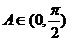 ∴
∴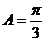
(Ⅱ)∵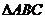 为锐角三角形且
为锐角三角形且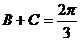 ∴
∴
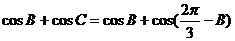
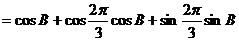
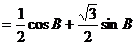
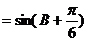
∵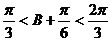 ∴
∴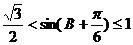 即
即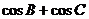 的取值范围是
的取值范围是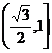
15.给出下列五个命题:
①命题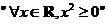 的否定是
的否定是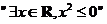 ;
;
②若等差数列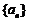 前
前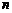 项和为
项和为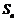 ,则三点
,则三点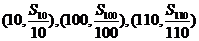 共线;
共线;
③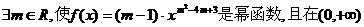 上单调递减;
上单调递减;
④在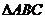 中,若
中,若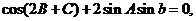 则
则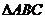 一定是等腰三角形。
一定是等腰三角形。
⑤函数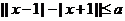 恒成立,则实数
恒成立,则实数 的取值范围是
的取值范围是 。
。
其中假命题的序号是 。(填上所有假命题的序号) ①④
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com