
3.化简: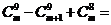 0 ; 4.若
0 ; 4.若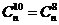 ,则
,则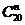 的值为 190 ;
的值为 190 ;
2.式子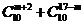 (
(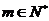 )的值的个数为 (A)
)的值的个数为 (A)
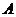 .
.
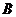 .
.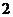
 .
.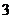
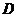 .
.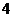
1.方程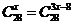 的解集为 (D)
的解集为 (D)
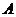 .
.
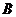 .
.
 .
.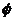
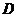 .
.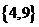
3.常用的等式: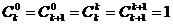 .
.
2.从特殊到一般的归纳思想;
补充:证明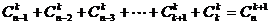 ;
;
其等价形式为: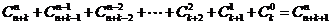 .
.
(二)新课讲解:
1.组合数的性质1: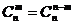 .
.
理解:一般地,从n个不同元素中取出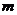 个元素后,剩下
个元素后,剩下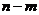 个元素.因为从n个不同元素中取出m个元素的每一个组合,与剩下的n - m个元素的每一个组合一一对应,所以从n个不同元素中取出m个元素的组合数,等于从这n个元素中取出n - m个元素的组合数,即:
个元素.因为从n个不同元素中取出m个元素的每一个组合,与剩下的n - m个元素的每一个组合一一对应,所以从n个不同元素中取出m个元素的组合数,等于从这n个元素中取出n - m个元素的组合数,即: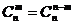 .
.
在这里,我们主要体现:“取法”与“剩法”是“一一对应”的思想。
证明:∵
又 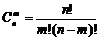 ,∴
,∴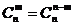 。
。
说明:①规定: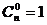 ;
;
②等式特点:等式两边下标同,上标之和等于下标;
③此性质作用:当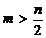 时,计算
时,计算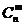 可变为计算
可变为计算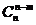 ,能够使运算简化,
,能够使运算简化,
例如: =
=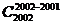 =
=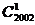 =2002;
=2002;
④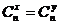
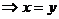 或
或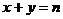 .
.
2.示例:(课本101例4)一个口袋内装有大小不同的7个白球和1个黑球,
(1)从口袋内取出3个球,共有多少种取法?
(2)从口袋内取出3个球,使其中含有1个黑球,有多少种取法?
(3)从口袋内取出3个球,使其中不含黑球,有多少种取法?
解:(1)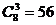 ;(2)
;(2)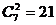 ;(3)
;(3)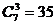 .
.
引导学生发现: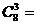
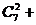
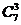 ,并要求用组合的知识解释,根据计算的结果猜想一般的结论,并予以证明。
,并要求用组合的知识解释,根据计算的结果猜想一般的结论,并予以证明。
我们可以这样解释:从口袋内的8个球中所取出的3个球,可以分为两类:一类含有1个黑球,一类不含有黑球.因此根据分类计数原理,上述等式成立。
一般地,从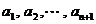 这n+1个不同元素中取出m个元素的组合数是
这n+1个不同元素中取出m个元素的组合数是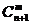 ,这些组合可以分为两类:一类含有元素
,这些组合可以分为两类:一类含有元素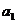 ,一类不含有
,一类不含有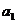 .含有
.含有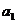 的组合是从
的组合是从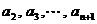 这n个元素中取出m -1个元素与
这n个元素中取出m -1个元素与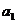 组成的,共有
组成的,共有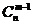 个;不含有
个;不含有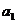 的组合是从
的组合是从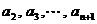 这n个元素中取出m个元素组成的,共有
这n个元素中取出m个元素组成的,共有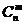 个.根据分类计数原理,可以得到组合数的另一个性质.在这里,我们主要体现从特殊到一般的归纳思想,“含与不含其元素”的分类思想.
个.根据分类计数原理,可以得到组合数的另一个性质.在这里,我们主要体现从特殊到一般的归纳思想,“含与不含其元素”的分类思想.
3.组合数的性质2: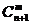 =
=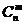 +
+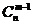 .
.
证明: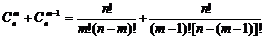
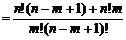
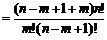
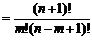

∴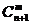 =
=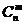 +
+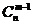 .
.
说明:①公式特征:下标相同而上标差1的两个组合数之和,等于下标比原下标多1而上标与大的相同的一个组合数;
②此性质的作用:恒等变形,简化运算。
4.例题分析:
例1 (1)计算: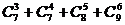 ;
;
(2)求证: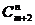 =
=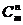 +
+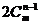 +
+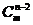 .
.
解:(1)原式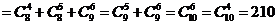 ;
;
证明:(2)右边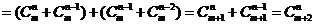
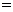 左边。
左边。
例2 解方程:(1)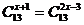 ;(2)解方程:
;(2)解方程: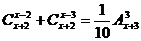 .
.
解:(1)由原方程得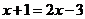 或
或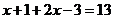 ,∴
,∴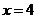 或
或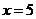 ,
,
又由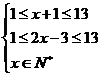 得
得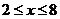 且
且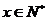 ,∴原方程的解为
,∴原方程的解为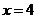 或
或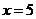 。
。
注:上述求解过程中的不等式组可以不解,直接把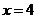 和
和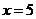 代入检验,这样运算量小得多.
代入检验,这样运算量小得多.
(2)原方程可化为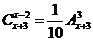 ,即
,即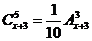 ,∴
,∴ ,
,
∴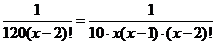 ,∴
,∴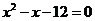 ,解得
,解得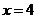 或
或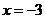 ,
,
经检验: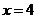 是原方程的解。
是原方程的解。
2.进一步理解排列与组合的区别和联系,熟练掌握组合数的计算公式,并且能够运用公式解决一些简单的应用问题。
假定你是李华, 你的英国朋友Peter来信向你咨询如何才能学好中文. 请你根据下列要点写回信.
要点: 1. 参加中文学习班; 2. 看中文书刊、电视; 3. 学唱中文歌曲; 4. 交中国朋友。
注意: 1.词数100左右; 2. 可适当增加细节,以使行文连贯; 3. 开头语已为你写好。
June 8, 2008
Dear Peter,
I'm glad to recerve your letter asking for my advice on how to learn Chinese well.
Best wishes,
Li Hua

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com