8．(本小题满分10分)已知某类型的高射炮在它们控制的区域内击中具有某种速度敌机的概率为20%.

①假定有5门这种高射炮控制某个区域，求敌机进入这个区域后被击中的概率；

②要使敌机一旦进入这个区域内有90%以上的概率被击中，至少需要布置几门这类高射炮？

解．①设敌机被各炮击中的事件分别记为A1、A2、A3、A4、A5，那么5门炮都来击中敌机的事件为

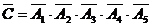，因各炮射击的结果是相互独立的，所以

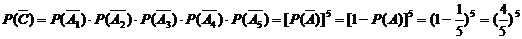
因此敌机被击中的概率为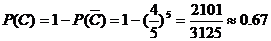……………………5分

②设至少需要置n门高射炮才能有90%以上的概率击中敌机，由①可知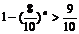 即8n＜10n－1

两边取常用对数，得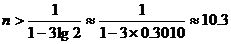　 ∴n≥11.

即至少需布置11门高射炮才能有90%以上的概率击中敌机.…………………………………………10分

7．有如图连接的6个元件，它们断电的概率第一个为P1=0.6，第二个为P2=0.2，其余四个都为P=0.3.求电器断电的概率.

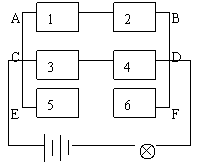
解．分别证AB、CD、EF三线路断电事件为M、N、G，每个线路断电二个元件至少有一个断电，且它们

　　 是相互独立的，于是P(M)=1－(1－0.6)(1－0.2)=1－0.4×0.8=0.68…………………………3分

P(N)=P(G)=1－(1－0.3)(1－0.3)=1－0.7×0.7=0.51…………………………………………7分

由于事件M、N、G相互独立，所以电器断电的概率P(M·N·G)=0.68×0.51×0.51=0.177…10分

6．某城市的发电厂有五台发电机组，每台机组在一个季度内停机维修

率为.已知两台以上机组停机维修，将造成城市缺电.计算：

①该城市在一个季度内停电的概率； ②该城市在一个季度内缺电的概率.

解．①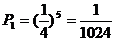，即五台机组都维修停电的概率为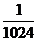…………………………………3分

②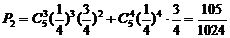，即两台以上机组维修缺电的概率为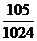……9分

5．(本小题满分9分)6位同学到A、B、C三处参加社会实践，求：

①每处均有2位同学的概率；　 ②A处恰有3位同学的概率.

解．①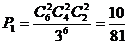，即每处均有2位同学的概率为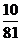……………………………………4分

②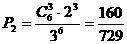，即A处恰有3位同学的概率为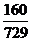…………………………………9分

4．甲袋内有8个白球，4个红球；乙袋内有6个白球，4个红球.现从两个袋内各取1个球.计算：

①取得两个球颜色相同的概率；

②取得两个球颜色不相同的概率.

解．①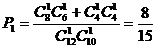，即取得两个球颜色相同的概率为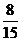…………………………4分

②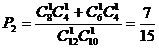，即取得两个球颜色不相同的概率为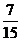………………………8分

3.某人进行打靶练习，共射击10次，其中有2次中10环，有3次中9环，有4次中8环，有1次未中靶. 试计算此人中靶的概率；假若此人射击一次，试问

中靶8环以上的概率是多少？

解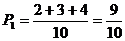．　 即中靶的概率为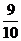………………………………………………4分

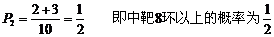　　　　 …………………………………………8分

2.甲射中目标的概率是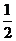,乙射中目标的概率是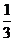,丙射中目标的概率是.

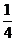现在三人同时射击目标,则目标被击中的概率.,

解.设A=甲射中目标,B=乙射中目标,C=丙射中目标,∵A,B,C相互独立,目标被击中则A,B,C中至少一个发生,它的对立事件是目标未击中即:

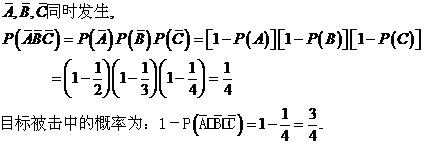
1.甲乙两人独立地破译一个密码,他们能破译密码的概率分别是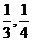.求

①.两人都译出密码的概率. ②.两人都译不出密码的概率.

③.恰有一人译出密码的概率. ④.至多一人译出密码的概率

⑤.要达到译出密码的概率为,至少需要乙这样的人多少个.

解.设A=甲译出密码,B=乙译出密码,C=密码破译,A,B独立.

①. P(C)=P(AB)=P(A)P(B)==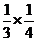

②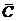.P(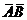)=P()=P(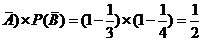

③∵A,B是独立事件,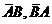也是独立且互斥的事件,

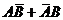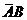∴C=,　　 P(C)=P()+P()=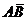

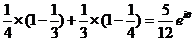
④.至多一个人译出密码, 即两人都译不出密码或恰有一人译出密码.

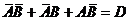∴P(D)=P()=

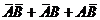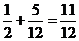
⑤．设n个乙这样的人都译不出密码的概率

10、右图是化学实验常用装置之一,若气体从右管进入，可用来收集的气体是　 　

A．NO 　　　　B． NO₂　　　 C．Cl₂ 　　D．NH₃

9、在常温常压下，下列各组气体不能共存的是 　　　　　　　　　　　　　　

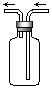A．SO₂与O₂　　　　　 B．CO与O₂

C．NH₃与HCl　　　　 D．NO与O₂