
7.集合M={x|x=sin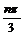 ,n∈Z},N={ x|x=cos
,n∈Z},N={ x|x=cos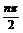 ,n∈Z },M∩N= ( )
,n∈Z },M∩N= ( )
A.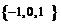 B.
B.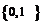
C.{0}
D.
6.已知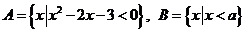 , 若
, 若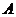 (/
(/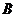 , 则实数
, 则实数 的取值范围是( )
的取值范围是( )
A. 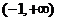 B.
B.
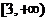 C.
C.
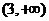 D.
D.
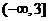
5.设M,P是两个非空集合,定义M与P的差集为M-P={x|x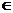 M且x
M且x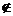 p},则M-(M-P)等于( )
p},则M-(M-P)等于( )
A. P B. M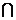 P C. M
P C. M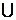 P D. M
P D. M
4.设集合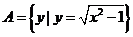 ,
,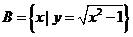 ,则下列关系中正确的是( )
,则下列关系中正确的是( )
A. B.
B.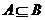 C.
C.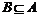 D.
D.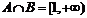
3.设集合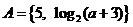 ,集合
,集合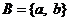 ,若
,若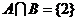 , 则
, 则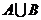 等于( )
等于( )
A.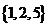 B.
B.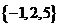
C.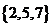 D.
D.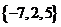
2.当x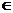 R,下列四个集合中是空集的是( )
R,下列四个集合中是空集的是( )
A. {x|x2-3x+2=0} B. {x|x2<x}
C. {x|x2-2x+3=0}
C. {x|sinx+cosx=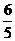 }
}
1.设全集U=R,A={x∈N︱1≤x≤10},B={ x∈R︱x 2+ x-6=0},则下图中阴影表示的集合为( )
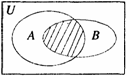 A.{2} B.{3} C.{-3,2}
D.{-2,3}
A.{2} B.{3} C.{-3,2}
D.{-2,3}
11.某足球队运动员进行射门训练,教练员规定:球员每次从中场向球门运球时,在距球门20m处进行第一次射门,若射中则重新运球;若不中,则在距球门15m处进行第二次射门,若射中则重新运球;若不中,则在距球门10m处进行第三次射门。每次运球最多射门三次。已知运动员在距球门20m处射门命中的概率是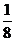 ,又射门命中的概率与运动员和球门之间的距离的平方成反比。问该运动员在每次运球过程中射门命中的概率能不能超过
,又射门命中的概率与运动员和球门之间的距离的平方成反比。问该运动员在每次运球过程中射门命中的概率能不能超过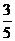 ?
?
12*.平面上有两个质点A(0,0), B(2,2),在某一时刻开始每隔1秒向上下左右任一方向移动一个单位。已知质点A向左,右移动的概率都是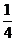 ,向上,下移动的概率分别是
,向上,下移动的概率分别是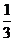 和P, 质点B向四个方向移动的概率均为q:
和P, 质点B向四个方向移动的概率均为q:
(1)求P和q的值;
(2)试判断至少需要几秒,A,B能同时到达D(1,2),并求出在最短时间同时到达的概率?
解:(1)由于质点向四个方向移动是一个必然事件,则:P= ;q=
;q=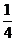 。
。
(2)至少需要3秒才可以同时到达D,则当经过3秒:
A到达D点的概率为: 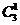 ·P(右)·P(上)·P(上)=
·P(右)·P(上)·P(上)=
设N(2,1);C(1,1);H(3,2);F(2,3);E(1,3);则经过3秒,B到达D的可能情景为:
DBD,DMD,DED,DCD,NBD,NCD,HBD,FED,FBD,共9种可能。
B到达D点的概率为:9×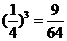
又B到达D点与A到达D点之间没有影响,则A,B同时到达的概率为: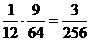
13*.有人玩掷硬币走跳跳棋的游戏,已知硬币出现正反面的概率都是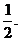 棋盘上标有第0站、第1站、第2站、…第100站. 一枚棋子开始在第0站,棋手每掷一次硬币,棋子向前跳动一次. 若掷出正面,棋向前跳一站(从k到k+1);若掷出反面,棋子向前跳二站(从k到k+2),直到棋子跳到第99站(胜利大本营)或跳到第100站(失败集中营)时,该游戏结束. 设棋子跳到第n站的概率为Pn.
棋盘上标有第0站、第1站、第2站、…第100站. 一枚棋子开始在第0站,棋手每掷一次硬币,棋子向前跳动一次. 若掷出正面,棋向前跳一站(从k到k+1);若掷出反面,棋子向前跳二站(从k到k+2),直到棋子跳到第99站(胜利大本营)或跳到第100站(失败集中营)时,该游戏结束. 设棋子跳到第n站的概率为Pn.
(1)求P0,P1,P2的值; (2)求证: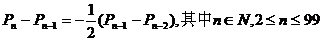 ;
;
(3)求P99及P100的值.
解:(1)棋子开始在第0站为必然事件,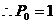 ,第一次掷硬币出现正面,棋子跳到第1站,其概率为
,第一次掷硬币出现正面,棋子跳到第1站,其概率为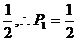 ,棋子跳到第二站应从如下两方面考虑:①
二次掷硬币都出现正面,其概率为
,棋子跳到第二站应从如下两方面考虑:①
二次掷硬币都出现正面,其概率为 ;②第一次掷硬币出现反面,其概率为
;②第一次掷硬币出现反面,其概率为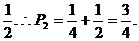
(2)棋子跳到第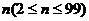 站的情况是下列两种,而且也只有两种:①棋子先到第n-2站,又掷出反面,其概率为
站的情况是下列两种,而且也只有两种:①棋子先到第n-2站,又掷出反面,其概率为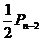 ;②棋子先到第n-1站,又掷出正面,其概率为
;②棋子先到第n-1站,又掷出正面,其概率为

(3)由(2)知,当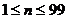 时,数列
时,数列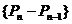 是首项为
是首项为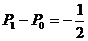 ,公比为
,公比为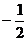 的等比数列.
的等比数列.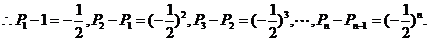
以上各式相加,得
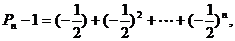
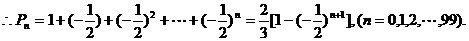

14*.袋中装有m个红球和n个白球,m≥n≥2,这些红球和白球除了颜色不同以外,其余都相同.从袋中同时取出2个球. (1)若取出是2个红球的概率等于取出的是一红一白的2个球的概率的整数倍,试证:
m必为奇数; (2)在m,n的数组中,若取出的球是同色的概率等于不同色的概率,试求 m+n≤40
的所有数组(m,n).
解:(1)设取出2个球是红球的概率是取出的球是一红一白2个球的概率的k倍(k为整数) 则有 ∴=kmn Þ m=2kn+1
∵k∈Z,n∈Z,∴m=2kn+1为奇数
(2)由题意,有 ∴=mn ∴m2-m+n2-n-2mn=0 即(m-n)2=m+n ∵m≥n≥2,所以m+n≥4 ∴2≤m-n≤<7
∴m-n的取值只可能是2,3,4,5,6; 相应的m+n的取值分别是4,9,16,25,36 即或或或或 解得或或或或 注意到m≥n≥2 ∴(m,n)的数组值为(6,3),(10,6),(15,10),(21,15)
10.某单位6个员工借助互联网开展工作,每个员工上网的概率都是0.5,且相互独立.
(1)求至少3人同时上网的概率;
(2)至少几人同时上网的概率小于0.3?
解析 (1)至少3人同时上网的概率等于1减去至多2人同时上网的概率,即

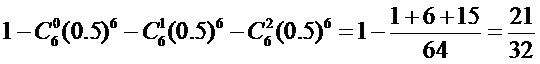
(2)至少4人同时上网的概率为
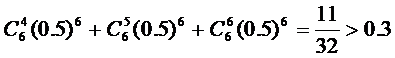
至少5人同时上网的概率为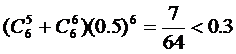 .因此,至少5人同时上网的概率小于0.3.
.因此,至少5人同时上网的概率小于0.3.
9.甲、乙两人进行乒乓球决赛,采取五局三胜制,即如果甲或乙无论谁先胜了三局,比
赛宣告结束,胜三局者为冠军.
假定每局甲获胜的概率是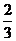 ,乙获胜的概率是
,乙获胜的概率是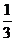 ,试求:
,试求:
(Ⅰ)比赛以甲3胜1败获冠军的概率;
(Ⅱ)比赛以乙3胜2败冠军的概率;
解:(Ⅰ)以甲3胜1败而结束比赛,甲只能在1、2、3次中失败1次,因此所求概率为: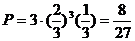
(Ⅱ)乙3胜2败的场合 ,因而所求概率为
,因而所求概率为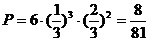
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com