
10.(2010山东聊城三中二模)
等差数列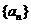 中,
中,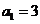 ,前
,前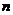 项和为
项和为 ,等比数列
,等比数列 各项均为正数,
各项均为正数, ,且
,且 ,
, 的公比
的公比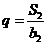
(1)求 与
与 ;
;
(2)求
2010年新课标省市高三数学模拟题分类
第三节 数列详解答案
9.(2010海南海口调研测试)
设数列 的前
的前 项和为
项和为 ,
, 为等比数列,且
为等比数列,且 ,
, .
.
(I)求数列 和
和 的通项公式;
的通项公式;
(II)设 ,求数列
,求数列 的前
的前 项和
项和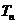 .
.
8.(2010英才苑模拟试卷)
设数列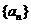 满足:
满足: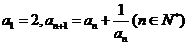 .
.
(I)证明: 对
对 恒成立;
恒成立;
(II)令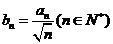 ,判断
,判断 与
与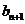 的大小,并说明理由.
的大小,并说明理由.
7.(2010北京宣武区一模)
已知数列 满足
满足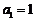 ,点
,点 在直线
在直线 上.
上.
⑴求数列 的通项公式;
的通项公式;
⑵若数列 满足
满足 ,求
,求 的值;
的值;
⑶对于⑵中的数列 ,求证:
,求证:
 .
.
6.(2010福建省调研测试)
已知数列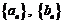 ,其中
,其中 ,数列
,数列 的前
的前 项和
项和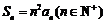 ,数列
,数列 满足
满足 .
.
⑴求数列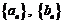 的通项公式;
的通项公式;
⑵是否存在自然数 ,使得对于任意
,使得对于任意 ,
, ,有
,有 恒成立?若存在,求出
恒成立?若存在,求出 的最小值;
的最小值;
⑶若数列 满足
满足 ,求数列
,求数列 的前
的前 项和
项和 .
.
5.(2010辽宁丹东高三阶段测试)
已知定义在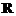 上的函数
上的函数 和数列
和数列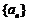 满足下列条件:
满足下列条件:
 ,
, ,
, ,…
,… ,
,
 ,
, ,
, ,…
,… ,
,
若 ,
, ,令
,令 .
.
(I)证明数列 是等比数列,并求数列
是等比数列,并求数列 的通项公式;
的通项公式;
(II)设 ,
, ,求使
,求使 取最大值时的
取最大值时的 值.
值.
4.(2010辽宁丹东二模)
数列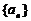 中,
中, ,
, .
.
(I)若 ,设
,设 ,求证数列
,求证数列 是等比数列,并求出数列
是等比数列,并求出数列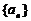 的通项公式;
的通项公式;
(II)若 ,
, ,
, ,用数学归纳法证明:
,用数学归纳法证明: .
.
3.(2010四川省模拟题)
已知数列 满足:
满足: ,
,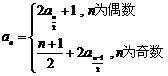 ,
, .
.
⑴求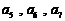 的值;
的值;
⑵设 ,试求数列
,试求数列 的通项公式;
的通项公式;
⑶对于任意的正整数 ,试讨论
,试讨论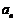 与
与 的大小关系.
的大小关系.
2.(2010北京西城区模拟)
设数列 为等比数列,数列
为等比数列,数列 满足
满足 ,
, ,已知
,已知 ,
, ,其中
,其中 .
.
⑴求数列 的首项和公比;
的首项和公比;
⑵当 时,求
时,求 ;
;
⑶设 为数列
为数列 的前
的前 项和,若对于任意的正整数
项和,若对于任意的正整数 ,都有
,都有 ,求实数
,求实数 的取值范围.
的取值范围.
1.(2010广东惠州一模)
已知数列 中,
中,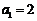 ,对于任意的
,对于任意的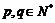 ,有
,有
(1)求数列 的通项公式;
的通项公式;
(2)若数列 满足:
满足: ……
…… ,求数列
,求数列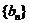 的通项公式;
的通项公式;
(3)设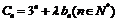 ,是否存在实数
,是否存在实数 ,当
,当 时,
时, 恒成立,若存在,
恒成立,若存在,
求实数 的取值范围,若不存在,请说明理由。
的取值范围,若不存在,请说明理由。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com