
10.

9. 解:(I)当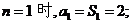 ………………(2分)
………………(2分)
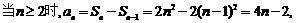
故{an}的通项公式为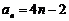 ;
………………(4分)
;
………………(4分)
设{bn}的通项公式为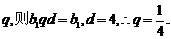
故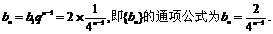 ………………(6分)
………………(6分)
(II)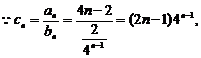 ………………(8分)
………………(8分)
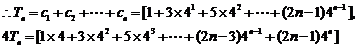
两式相减得 ………………(10分)
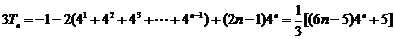
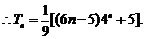 ………………(12分)
………………(12分)
8. 解:(1)证法一:当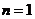 时,
时,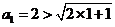 ,不等式成立,
,不等式成立,
假设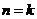 时,
时,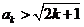 成立 (2分),
成立 (2分),
当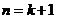 时,
时,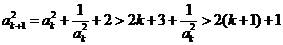 .(5分)
.(5分)
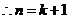 时,
时,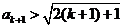 时成立
时成立
综上由数学归纳法可知,  对一切正整数成立 (6分)
对一切正整数成立 (6分)
证法二:当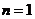 时,
时,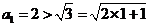 ,结论成立;
,结论成立;
假设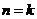 时结论成立,即
时结论成立,即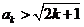 (2分) 当
(2分) 当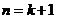 时,
时,
由函数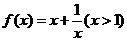 的单增性和归纳假设有
的单增性和归纳假设有
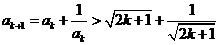 (4分),
(4分),
因此只需证: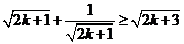 ,
,
而这等价于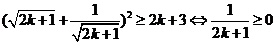 ,
,
显然成立,所以当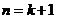 是,结论成立;
是,结论成立;
综上由数学归纳法可知,  对一切正整数成立 (6分)
对一切正整数成立 (6分)
证法三:由递推公式得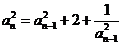 ,
,
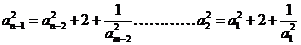 (2分)
(2分)
上述各式相加并化简得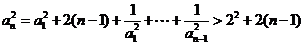
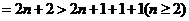 (4分)
(4分)
又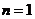 时,
时, 显然成立, 故
显然成立, 故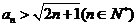 (6分)
(6分)
7. ⑴∵点 在直线
在直线 上,∴
上,∴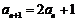
∴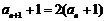 ,
,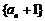 是以
是以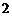 为首项,
为首项,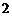 为公比的等比数列,
为公比的等比数列,
∴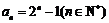
⑵∵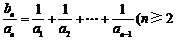 且
且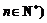 ,
,
∴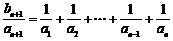 ,
,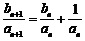
∴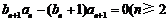 且
且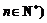 ;
;
当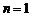 时,
时,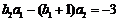 .
.
⑶由⑵知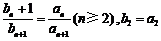
∴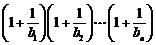
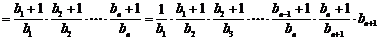
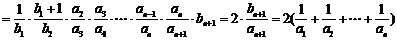
∵ 时,
时,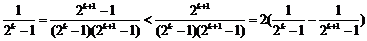
∴
 ,
,
∴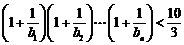 ,
,
即 .
.
6. ⑴因为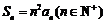 .
.
当 时,
时,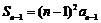 ;
;
所以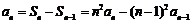 .
.
所以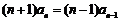 .即
.即 .
.
又 ,
,
所以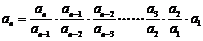
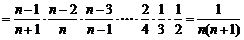 .
.
当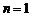 时,上式成立.
时,上式成立.
因为 ,
,
所以 是首项为
是首项为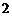 ,公比为
,公比为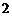 的等比数列,故
的等比数列,故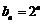 ;
;
⑵由⑴知,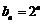 .
.
则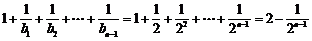 ,
,
假设存在自然数 ,使得对于任意
,使得对于任意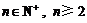 ,有
,有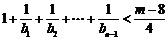 恒成立,
恒成立,
即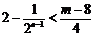 恒成立,由
恒成立,由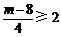 ,解得
,解得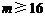 ,
,
所以存在自然数 ,使得对于任意
,使得对于任意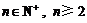 ,
,
有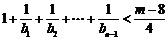 恒成立,此时,
恒成立,此时, 的最小值为16.
的最小值为16.
⑶当 为奇数时,
为奇数时,
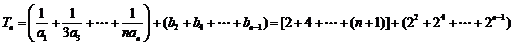
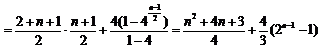 ;
;
当 为偶数时,
为偶数时,
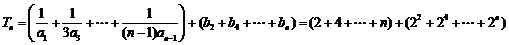
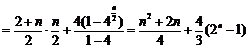 ;
;
因此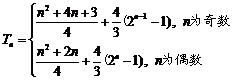 .
.
5. 解:(I)∵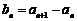 ,∴
,∴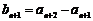 ,
,
∴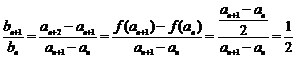
∴数列 是等比数列,
……………(4分)
是等比数列,
……………(4分)
∵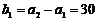 ∴
∴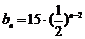 .
……………(6分)
.
……………(6分)
(II)方法1: 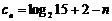 ,∵
,∵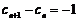 ,∴数列
,∴数列 是递减的等差数列,
是递减的等差数列,
……………(8分)
令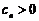 得
得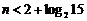 ,∵
,∵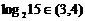 ,∴
,∴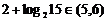 ………(10分)
………(10分)
∴数列 的前5项都是正的,第6项开始全部是负的,∴
的前5项都是正的,第6项开始全部是负的,∴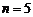 时,
时, 取最大值.
取最大值.
……………(12分)
方法2: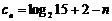 ,∵
,∵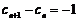 ,∴数列
,∴数列 是等差数列,
是等差数列,
……………(8分)
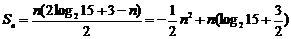 ,对称轴直线
,对称轴直线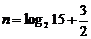 ,
,
∵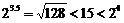 ,∴
,∴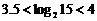 ,
……………(10分)
,
……………(10分)
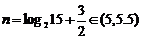 ∵
∵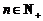 ,∴
,∴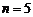 时,
时, 取最大值. …………(12分)
取最大值. …………(12分)
4. (I)
证明:∵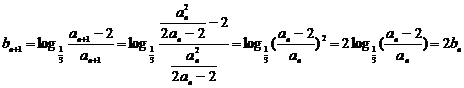 ,
,
…………(2分)
∵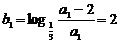 ,∴数列
,∴数列 是首项为2,公比为2的等比数列,
是首项为2,公比为2的等比数列,
…………(4分)
∴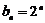 ,即
,即 ,得
,得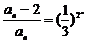 ,所以
,所以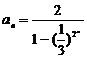 .
.
…………(6分)
(II)证明:(i)当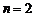 时,∵
时,∵ ,∴
,∴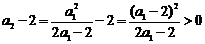 ,
,
∴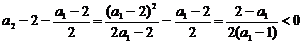 ,
,
∴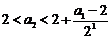 ,不等式成立; …………(8分)
,不等式成立; …………(8分)
(ii)假设当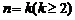 时,
时,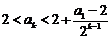 成立,
成立,
那么,当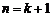 时,去证明
时,去证明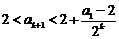
∵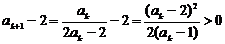 ,∴
,∴ ;
;
∵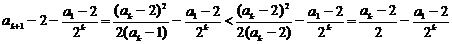 ,
,
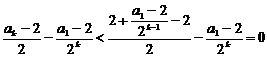
∴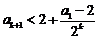 ;∴
;∴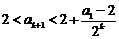 ,
,
所以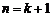 不等式也成立,
不等式也成立,
由(i)(ii)可知,不等式成立. …………(12分)
3. ⑴∵ ,
,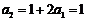 ,
,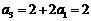 ,
,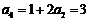 ,
,
∴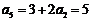 ;
;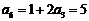 ;
;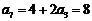 .
.
⑵由题设,对于任意的正整数 ,都有:
,都有:
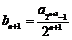
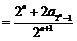
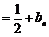 ,
,
∴ .
.
∴数列 是以
是以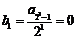 为首项,
为首项,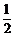 为公差的等差数列.
为公差的等差数列.
∴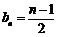 .
.
⑶对于任意的正整数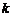 ,
,
当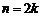 或
或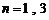 时,
时,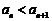 ;
;
当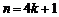 时,
时,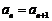 ;
;
当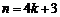 时,
时,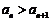 .
.
证明如下:
首先,由 ,
, ,
,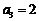 ,
,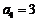 可知
可知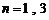 时,
时,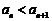 ;
;
其次,对于任意的正整数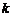 ,
,
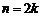 时,
时,
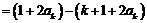
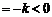 ;
;
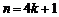 时,
时,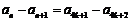
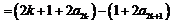
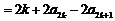
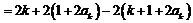
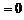
所以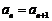 .
.
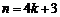 时,
时,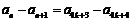
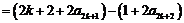
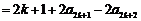
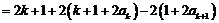
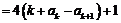
事实上,我们可以证明:对于任意正整数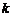 ,
,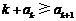 …(*)(证明见后),
…(*)(证明见后),
所以此时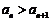 .
.
综上可知:结论得证.
对于任意正整数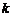 ,
,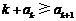 (*)的证明如下:
(*)的证明如下:
ⅰ)当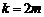 (
(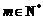 )时,
)时,
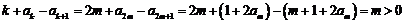 ,满足(*)式.
,满足(*)式.
ⅱ)当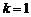 时,
时,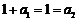 ,满足(*)式.
,满足(*)式.
ⅲ)当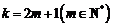 时,
时,
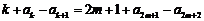
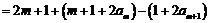
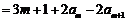
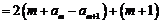
于是只须证明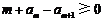 ,如此递推,可归结为ⅰ)或ⅱ)的情形,
,如此递推,可归结为ⅰ)或ⅱ)的情形,
于是(*)得证.
2. ⑴由已知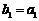 ,所以
,所以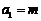 ;
;
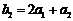 ,所以
,所以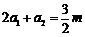 ,解得
,解得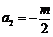 ;
;
所以数列 的公比
的公比 ;
;
⑵当 时,
时,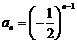 ,
,
 ,………………………①,
,………………………①,
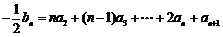 ,……………………②,
,……………………②,
②-①得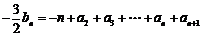 ,
,
所以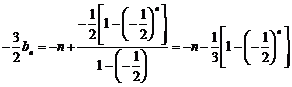 ,
,
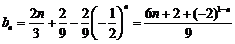 .
.
⑶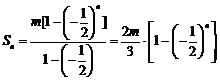 ,
,
因为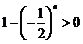 ,所以由
,所以由 得
得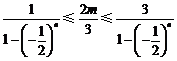 ,
,
注意到,当n为奇数时,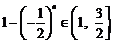 ;当
;当 为偶数时,
为偶数时,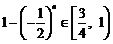 ,
,
所以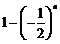 最大值为
最大值为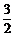 ,最小值为
,最小值为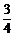 .
.
对于任意的正整数n都有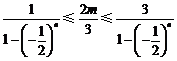 ,
,
所以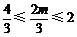 ,解得
,解得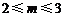 ,
,
即所求实数m的取值范围是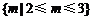 .
.
1. 解:(1)取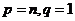 ,则
,则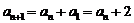 ∴
∴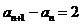 (
( )
)
∴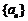 是公差为
是公差为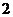 ,首项为
,首项为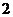 的等差数列
∴
的等差数列
∴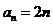 …………4分
…………4分
(2)∵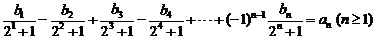 ①
①
∴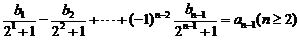 ②
②
①-②得: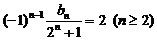 ∴
∴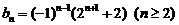 …………6分
…………6分
当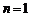 时,
时,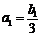 ∴
∴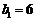 ,满足上式
∴
,满足上式
∴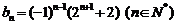 …………8分
…………8分
(3)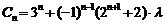 假设存在
假设存在 ,使
,使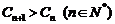
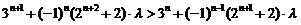 .
.
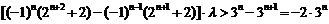 .
. 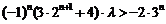 .
.
当 为正偶函数时,
为正偶函数时,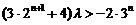 恒成立,
恒成立,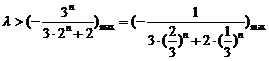 ∴
∴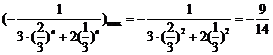 .∴
.∴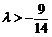 …………11分
…………11分
当 为正奇数时,
为正奇数时,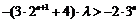 恒成立.∴
恒成立.∴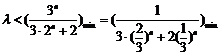
∴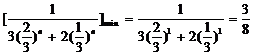 .∴
.∴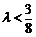 .
.
综上可知,存在实数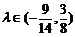 .使
.使 时,
时,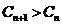 恒成立. …………14分
恒成立. …………14分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com