2.平移公式

设点P(x,y)按照给定的向量a＝(h,k)平移后得到新点，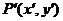

则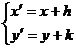

容易看到，公式中是用旧点的坐标和平移向量的坐标来表示新点坐标的，从向量的角度可以理解为向量坐标等于终点(新点)坐标减去起点(旧点)坐标，故公式也可变形为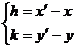

1.平移的概念

设F为平面内一个图形，将F上所有的点按照同一方向，移动同样的长度，得到，这个过程叫做图形的平移.

在图形平移过程中，自一点都是按照同一方向移动同样的长度，所以我们有两点思考：

其一，平移所遵循的“长度”和“方向”正是向量的两个本质特征，因此，从向量的角度看，一个平移就是一个向量.

其二，由于图形可以看成点的集合，故认识图形的平移，就其本质来讲，就是要分析图形上点的平移.

9.两向量夹角的余弦()　 　

cosq=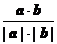

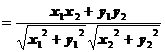
8.向量垂直的判定

设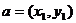，，则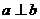　

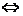
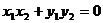
7.平面内两点间的距离公式

(1)设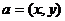，则或

(2)如果表示向量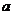的有向线段的起点和终点的坐标分别为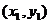、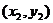，那么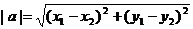(平面内两点间的距离公式)

6．两个向量的数量积等于它们对应坐标的乘积的和

，

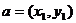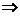
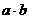
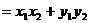
5． 平面向量数量积的运算律

交换律：a × b = b × a

数乘结合律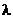：(a)×b =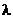(a×b) = a×(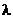b)

分配律：(a + b)×c = a×c + b×c

4．两个向量的数量积的性质：

设a、b为两个非零向量，e是与b同向的单位向量

1°e×a = a×e =|a|cosq；2°a^b Û a×b = 0

3°当a与b同向时，a×b = |a||b|；当a与b反向时，a×b = -|a||b|

　特别的a×a = |a|²或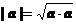

4°cosq =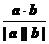 ；5°|a×b| ≤ |a||b|

3．向量的数量积的几何意义：

数量积a×b等于a的长度与b在a方向上投影|b|cosq的乘积

1．两个非零向量夹角的概念

已知非零向量a与b，作＝a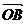，＝b，则∠AOB＝θ(0≤θ≤π)叫a与b的夹角.

(0≤θ≤π).并规定0与任何向量的数量积为0