
2.(2006全国Ⅰ)抛物线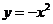 上的点到直线
上的点到直线 距离的最小值是 ( )
距离的最小值是 ( )
A 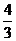 B
B
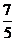 C
C 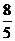 D
D 
1.(2004全国I)设抛物线y2=8x的准线与x轴交于点Q,若过点Q的直线l与抛物线有公共点,则直线l 的斜率的取值范围是 ( )
A.[-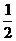 ,
,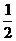 ] B.[-2,2] C.[-1,1] D.[-4,4]
] B.[-2,2] C.[-1,1] D.[-4,4]
5.弦长公式:
圆锥曲线与直线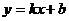 交于A(x1,y1),B(x2,y2),则弦长
交于A(x1,y1),B(x2,y2),则弦长
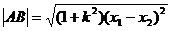 ;
;
与直线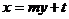 A(x1,y1),B(x2,y2),则弦长
A(x1,y1),B(x2,y2),则弦长
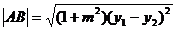

4.涉及直线与圆锥曲线相交弦的问题:
相交弦的长,弦所在直线的方程、弦的中点的轨迹等,这可以利用“点差法”,“设而不求”、 韦达定理、整体代入等方法求解。
3. 涉及到圆锥曲线焦点弦、焦半径的问题,首先考虑第二定义和焦半径公式。
2.直线与圆锥曲线有无公共点或有几个公共点的问题:
可以转化为它们所对应的方程构成的方程组是否有解或解的个数问题,往往通过消元转化为讨论一元二次方程的解的问题或一元二次函数的最值问题,运用韦达定理,中点公式,设而不求时必须Δ≥0,必须注意解的存在性和转化的等价性,用好化归与等价转化思想.
当直线与抛物线的对称轴平行或与双曲线的渐近线平行时,消元后得到的是一元一次方程,只有一个解,即直线与抛物线或双曲线有且只有一个交点.
1.直线与圆锥曲线的位置关系主要是:公共点、相交弦或焦点弦问题以及它们的综合运用.
5.会利用“设点代点、设而不求”的方法求弦所在直线的方程(如中点弦、相交弦等)、弦的中点的轨迹等.
4.会用弦长公式|AB|=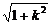 |x2-x1|求弦的长;
|x2-x1|求弦的长;
3.会利用圆锥曲线的焦半径公式解决焦点弦的问题 掌握求焦半径以及利用焦半径解题的方法;
掌握求焦半径以及利用焦半径解题的方法;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com