1.重点：“百家争鸣”局面出现的历史意义；孔子、孟子、荀子的主要观点，了解儒家思想的形成。

知识与能力：知道诸子百家，认识春秋战国时期“百家争鸣”局面形成的重要意义；了解孔子、孟子和荀子的主要观点，理解儒家思想的形成。

过程与方法：适度引入古代中国政治发展与传统文化方面的材料 ，启发学生思考百家争鸣局面形成的重要意义。以列表的方法，从时代、主要观点、影响等方面，指导学生归纳孔子、孟子和荀子的主要内容。以百家争鸣为主题，组织学生谈一谈继承中国传统文化思想的认识和感受。组织一次“我读《论语》的读书活动”。

情感态度与价值观：感受中国古代思想的博大精深：通过学习早期儒家的民本思想，培养学生的人文关怀精神；了解儒家文化是我国传统文化的最主要部分，认识其在世界文化史上的地位和对后世的影响；联系现实，使学生正确对待儒家传统文化，发挥其在当代的积极意义。

22.(2008·南京模拟)已知函数y=f(x)是定义在区间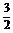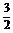［-，］上的偶函数，且

x∈［0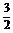，］时，f(x)=-x²-x+5.　

(1)求函数f(x)的解析式；　

(2)若矩形ABCD的顶点A，B在函数y=f(x)的图象上，顶点C，D在x轴上，求矩形ABCD面积的最大值.　

21.已知定义域为R的函数f(x)满足f(f(x)-x²+x)=f(x)-x²+x.　

(1)若f(2)=3,求f(1);又若f(0)=a,求f(a);　

(2)设有且仅有一个实数x₀,使得f(x₀)=x₀,求函数f(x)解析表达式.　

20.设a,b∈R，且a≠2,定义在区间(-b,b)内的函数f(x)=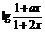是奇函数.　

(1)求b的取值范围；　

(2)讨论函数f(x)的单调性.　

19.(2008·深圳模拟)据调查，某地区100万从事传统农业的农民，人均收入3 000元，为了增加农民的收入，当地政府积极引进资本，建立各种加工企业，对当地的农产品进行深加工，同时吸收当地部分农民进入加工企业工作，据估计，如果有x (x＞0)万人进企业工作，那么剩下从事传统农业的农民的人均收入有望提高2x%,而进入企业工作的农民的人均收入为3 000a元 (a＞0).　

(1)在建立加工企业后，要使从事传统农业的农民的年总收入不低于加工企业建立前的农民的年总收入，试求x的取值范围；　

(2)在(1)的条件下，当地政府应该如何引导农民(即x多大时)，能使这100万农民的人均年收入达到最大.　

18.等腰梯形ABCD的两底分别为AB=10，CD=4，两腰AD=CB=5，动点P由B点沿折线BCDA向A运动，设P点所经过的路程为x，三角形ABP的面积为S　

(1)求函数S=f(x)的解析式；　

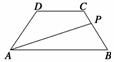(2)试确定点P的位置，使△ABP的面积S最大.　

17．设直线x=1是函数f(x)的图象的一条对称轴，对于任意x∈R，f(x+2)=-f(x),当-1≤x≤1时，f(x)=x³.

(1)证明：f(x)是奇函数；　

(2)当x∈［3，7］时，求函数f(x)的解析式.　

16.(2008·福州模拟)对于函数f(x)定义域中任意的x₁,x₂ (x₁≠x₂),　

有如下结论：　

①f(x₁+x₂)=f(x₁)f(x₂);　

②f(x₁·x₂)=f(x₁)+f(x₂);　

③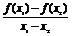＞0;　

④f()＜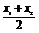

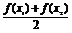
当f(x)=2^x时，上述结论中正确结论的序号是　　　　　 .　

15.(2008·通州模拟)用二分法求方程x³-2x-5=0在区间［2，3］内的实根，取区间中点x₀=2.5,那么下一个有实根的区间是　　　 .　

答案 (2，2.5)