
6. 如图所示,在光滑四分之一圆弧轨道的顶端a点,质量为m的物块(可视为质点)由静止开始下滑,经圆弧最低点b滑上粗糙水平面,圆弧轨道在b点与水平轨道平滑相接,物块最终滑至c点停止.若圆弧轨道半径为R,物块与水平面间的动摩擦因数为μ,下列说法正确的是( )
如图所示,在光滑四分之一圆弧轨道的顶端a点,质量为m的物块(可视为质点)由静止开始下滑,经圆弧最低点b滑上粗糙水平面,圆弧轨道在b点与水平轨道平滑相接,物块最终滑至c点停止.若圆弧轨道半径为R,物块与水平面间的动摩擦因数为μ,下列说法正确的是( )
A.物块滑到b点时的速度为
B.物块滑到b点时对b点的压力是2mg
C.c点与b点的距离为
D.整个过程中物块机械能损失了mgR
5.如图所示,一轻弹簧直立于水平地面上,质量为m的小球从距离弹簧上端B点h高处的A点自由下落,在C点处小球速度达到最大.x0表示B、C两点之间的距离;Ek表示小球在C处的动能.若改变高度h,则下列表示x0随h变化的图象和Ek随h变化的图象中正确的是( BC )
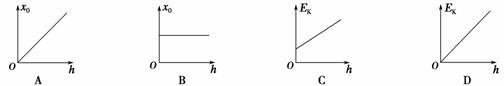
4.小球由地面竖直上抛,上升的最大高度为H,设所受阻力大小恒定,地面为零势能面.在上升至离地高度h处,小球的动能是势能的2倍,在下落至离地高度h处,小球的势能是动能的2倍,则h等于( )
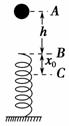 A. B. C. D.
A. B. C. D.
3.(2010·江门模拟)起重机将物体由静止举高h时,物体的速度为v,下列各种说法中正确的是(不计空气阻力)( )
A.拉力对物体所做的功,等于物体动能和势能的增量
B.拉力对物体所做的功,等于物体动能的增量
C.拉力对物体所做的功,等于物体势能的增量
D.物体克服重力所做的功,大于物体势能的增量
2.一个木块静止于光滑水平面上,现有一个水平飞来的子弹射入此木块并深入2 cm而相对于木块静止,同时间内木块被带动前移了1 cm,则子弹损失的动能、木块获得动能以及子弹和木块共同损失的动能三者之比为( )
A.3∶1∶2 B.3∶2∶1 C.2∶1∶3 D.2∶3∶1
1.质量不等,但有相同动能的两物体,在动摩擦因数相同的水平地面上滑行直到停止,则下列说法正确的有( )
A.质量大的物体滑行距离大 B.质量小的物体滑行距离大
C.质量大的物体滑行时间长 D.质量小的物体滑行时间长
4、巧用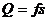 简解摩擦生热问题
简解摩擦生热问题
两个物体相互摩擦而产生的热量Q(或说系统内能的增加量)等于物体之间滑动摩擦力f与这两个物体间相对滑动的路程的乘积,即Q=fS相.利用这结论可以简便地解答高考试题中的“摩擦生热”问题。
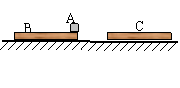 例4、如图所示,在一光滑的水平面上有两块相同的木板B和C。重物A(A视质点)位于B的右端,A、B、C的质量相等。现A和B以同一速度滑向静止的C,B与C发生正碰。碰后B和C粘在一起运动,A在C上滑行,A与C有摩擦力。已知A滑到C的右端面未掉下。试问:从B、C发生正碰到A刚移动到C右端期间,C所走过的距离是C板长度的多少倍?
例4、如图所示,在一光滑的水平面上有两块相同的木板B和C。重物A(A视质点)位于B的右端,A、B、C的质量相等。现A和B以同一速度滑向静止的C,B与C发生正碰。碰后B和C粘在一起运动,A在C上滑行,A与C有摩擦力。已知A滑到C的右端面未掉下。试问:从B、C发生正碰到A刚移动到C右端期间,C所走过的距离是C板长度的多少倍?
分析与解:设A、B、C的质量均为m。B、C碰撞前,A与B的共同速度为V0,碰撞后B与C的共同速度为V1。对B、C构成的系统,由动量守恒定律得:mV0=2mV1
设A滑至C的右端时,三者的共同速度为V2。对A、B、C构成的系统,由动量守恒定律得:2mV0=3mV2
设C的长度为L, A与C的动摩擦因数为μ,则据摩擦生热公式和能量守恒定律可得: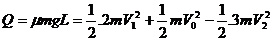
设从发生碰撞到A移至C的右端时C所走过的距离为S,则对B、C构成的系统据动能定理可得: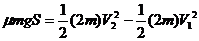
由以上各式解得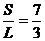 .
.
3、利用动能定理巧求机车脱钩问题
例3、总质量为M的列车,沿水平直线轨道匀速前进,其末节车厢质量为m,中途脱节,司机发觉时,机车已行驶L的距离,于是立即关闭油门,除去牵引力,如图13所示。设运动的阻力与质量成正比,机车的牵引力是恒定的。当列车的两部分都停止时,它们的距离是多少?
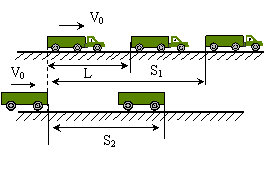 分析与解:此题用动能定理求解比用运动学、牛顿第二定律求解简便。
分析与解:此题用动能定理求解比用运动学、牛顿第二定律求解简便。
对车头,脱钩后的全过程用动能定理得:
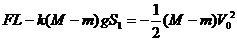
对车尾,脱钩后用动能定理得:
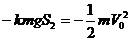
而 ,由于原来列车是匀速前进的,所以F=kMg
,由于原来列车是匀速前进的,所以F=kMg
由以上方程解得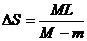 。
。
2、利用动能定理巧求动摩擦因数
 例2、如图所示,小滑块从斜面顶点A由静止滑至水平部分C点而停止。已知斜面高为h,滑块运动的整个水平距离为s,设转角B处无动能损失,斜面和水平部分与小滑块的动摩擦因数相同,求此动摩擦因数。
例2、如图所示,小滑块从斜面顶点A由静止滑至水平部分C点而停止。已知斜面高为h,滑块运动的整个水平距离为s,设转角B处无动能损失,斜面和水平部分与小滑块的动摩擦因数相同,求此动摩擦因数。
分析与解:滑块从A点滑到C点,只有重力和摩擦力做功,设滑块质量为m,动摩擦因数为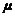 ,斜面倾角为
,斜面倾角为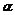 ,斜面底边长
,斜面底边长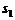 ,水平部分长
,水平部分长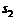 ,由动能定理得:
,由动能定理得:
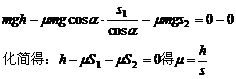
从计算结果可以看出,只要测出斜面高和水平部分长度,即可计算出动摩擦因数。
1、应用动能定理巧解多过程问题。
物体在某个运动过程中包含有几个运动性质不同的小过程(如加速、减速的过程),此时可以分段考虑,也可以对全过程考虑,如能对整个过程利用动能定理列式则使问题简化。
 例1、如图所示,斜面足够长,其倾角为α,质量为m的滑块,距挡板P为S0,以初速度V0沿斜面上滑,滑块与斜面间的动摩擦因数为μ,滑块所受摩擦力小于滑块沿斜面方向的重力分力,若滑块每次与挡板相碰均无机械能损失,求滑块在斜面上经过的总路程为多少?
例1、如图所示,斜面足够长,其倾角为α,质量为m的滑块,距挡板P为S0,以初速度V0沿斜面上滑,滑块与斜面间的动摩擦因数为μ,滑块所受摩擦力小于滑块沿斜面方向的重力分力,若滑块每次与挡板相碰均无机械能损失,求滑块在斜面上经过的总路程为多少?
分析与解:滑块在滑动过程中,要克服摩擦力做功,其机械能不断减少;又因为滑块所受摩擦力小于滑块沿斜面方向的重力分力,所以最终会停在斜面底端。
在整个过程中,受重力、摩擦力和斜面支持力作用,其中支持力不做功。设其经过和总路程为L,对全过程,由动能定理得:

得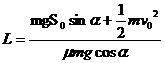
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com