
1、做加速度方向不变大小可变的变速直线运动的物体,下述情况中不可能出现的一项( )
A.速度和位移均增大,加速度为零时,速度达到最大
B.速度先减小后增大,速度变化越来越慢
C.速度逐渐减小,位移逐渐增大,速度减为零时,位移不是零
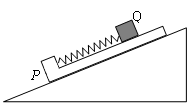 D.速度先增大、后减小,而位移一直在不断增大
D.速度先增大、后减小,而位移一直在不断增大
22. 已知数列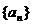 中,
中,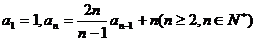 .且
.且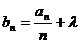 为等比数列;
为等比数列;
(Ⅰ) 求实数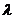 及数列
及数列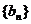 、
、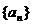 的通项公式;
的通项公式;
(Ⅱ) 若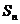 为
为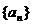 的前
的前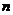 项和,求
项和,求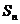 ;
;
(Ⅲ) 令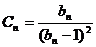 数列
数列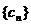 前
前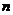 项和为
项和为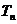 .求证:对任意
.求证:对任意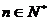 ,都有
,都有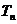 <3.
<3.
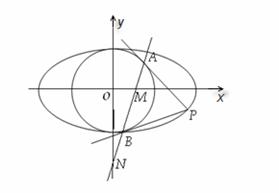
21.已知椭圆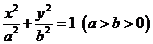 和圆
和圆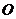 :
: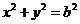 ,过椭圆上一点
,过椭圆上一点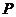 引圆
引圆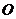 的两条切线,切点分别为
的两条切线,切点分别为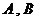 .
.
(Ⅰ)(ⅰ)若圆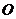 过椭圆的两个焦点,求椭圆的离心率
过椭圆的两个焦点,求椭圆的离心率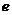 ;
;
(ⅱ)若椭圆上存在点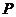 ,使得
,使得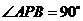 ,求椭圆离心率
,求椭圆离心率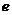 的取值范围;
的取值范围;
(Ⅱ)设直线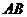 与
与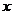 轴、
轴、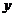 轴分别交于点
轴分别交于点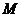 ,
,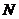 ,
,
求证: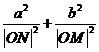 为定值.
为定值.
20.如图,直角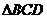 所在的平面垂直于正
所在的平面垂直于正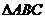 所在的平面,
所在的平面,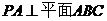 ,
,
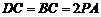 ,
,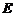 为
为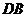 的中点;
的中点;
(Ⅰ)证明: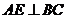 ;
;
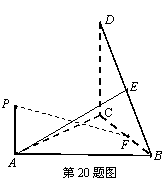 (Ⅱ)若点
(Ⅱ)若点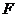 是线段
是线段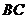 上的动点,设平面
上的动点,设平面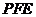 与平面
与平面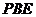 所成的平面角大小为
所成的平面角大小为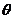 ,当
,当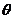 在
在 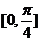 内取值时,求直线
内取值时,求直线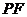 与平面
与平面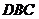 所成的角的正切值的范围.
所成的角的正切值的范围.

19.已知函数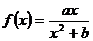 在
在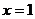 处取得极值2.
处取得极值2.
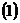 求函数的
求函数的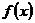 解析式
解析式
 当
当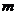 满足什么条件时,函数
满足什么条件时,函数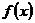 在
在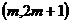 上是单调递增的
上是单调递增的
 若点
若点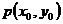 是此函数图像上任意一点,直线
是此函数图像上任意一点,直线 与此函数切于点
与此函数切于点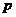 ,求直线
,求直线 的斜率
的斜率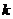 的取值范围。
的取值范围。
18.已知函数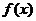 的定义域为
的定义域为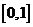 ,且同时满足:
,且同时满足:
(1)对任意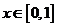 ,总有
,总有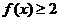 ;. (2)
;. (2)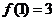 ;
;
(3)若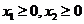 且
且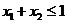 ,则有
,则有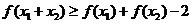 .
.
(I)求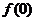 的值;
的值;
(II)判断函数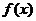 的单调性并给出证明;
的单调性并给出证明;
(III)设数列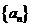 的前
的前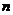 项和为
项和为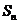 ,且满足
,且满足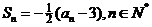 .
.
求证: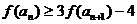 .
.

17. 设集合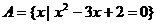 ,
,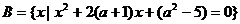 .
.
(1)若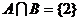 ,求实数
,求实数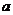 的值;
的值;
(2)若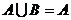 ,求实数
,求实数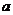 的取值范围.
的取值范围.
16.设集合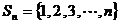 ,若
,若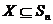 ,把
,把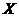 的所有元素的乘积称为
的所有元素的乘积称为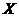 的容量(若
的容量(若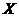 中只有一个元素,则该元素的数值即为它的容量,规定空集的容量为0).若
中只有一个元素,则该元素的数值即为它的容量,规定空集的容量为0).若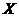 的容量为奇(偶)数,则称
的容量为奇(偶)数,则称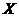 为
为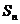 的奇(偶)子集.若
的奇(偶)子集.若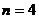 ,则
,则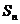 的所有偶子集的容量之和为_______.
的所有偶子集的容量之和为_______.
15.对任意的实数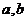 ,
,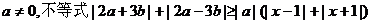 ,则实数x的取值范围是
.
,则实数x的取值范围是
.
14.已知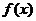 是定义在
是定义在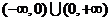 上的奇函数,当
上的奇函数,当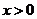 时,
时,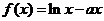 . 若函数
. 若函数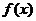 在其定义域上有且仅有四个不同的零点,则实数
在其定义域上有且仅有四个不同的零点,则实数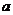 的取值范围是 .
的取值范围是 .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com