
22.解:(1)设P(x,y)是函数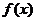 的图象上任意一点,则容易求得P点关于直线x=1的对称点为
的图象上任意一点,则容易求得P点关于直线x=1的对称点为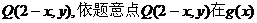 的图象上,
的图象上,
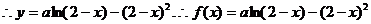 .………………2分
.………………2分
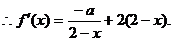
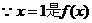 的一个极值点,
的一个极值点,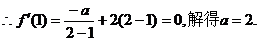
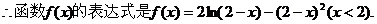 ………………4分
………………4分
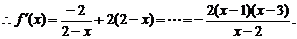
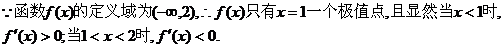
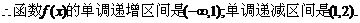 …………6分
…………6分
(2)由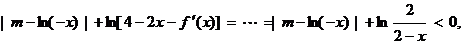
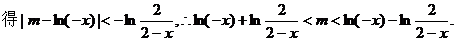 ……10分
……10分
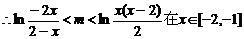 时恒成立.
时恒成立.
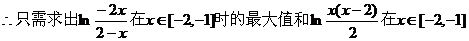 时的最小值,
时的最小值,
即可求得m的取值范围.
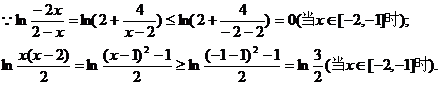
 ……………………………………………………14分
……………………………………………………14分
21.解:(Ⅰ)设椭圆的半焦距为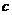 ,依题意
,依题意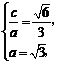
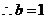 ,
,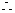 所求椭圆方程为
所求椭圆方程为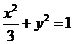 ---6分
---6分
(Ⅱ)设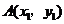 ,
,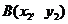 .(1)当
.(1)当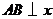 轴时,
轴时,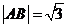 . -------------------8分
. -------------------8分
(2)当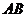 与
与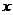 轴不垂直时,设直线
轴不垂直时,设直线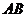 的方程为
的方程为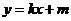 .由已知
.由已知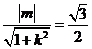 ,---------9分
,---------9分
得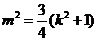 .---------10分
.---------10分
把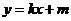 代入椭圆方程,整理得
代入椭圆方程,整理得 ,
,
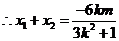 ,
,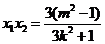 .
.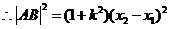
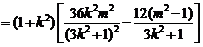
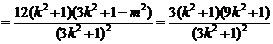
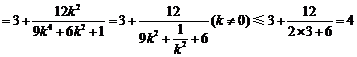 .
.
当且仅当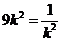 ,即
,即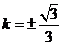 时等号成立.当
时等号成立.当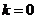 时,
时,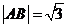 ,综上所述
,综上所述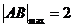 .
.
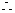 当
当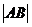 最大时,
最大时,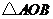 面积取最大值
面积取最大值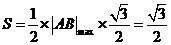 .---------------12分
.---------------12分
20.解:(1)从50名教师随机选出2名的方法数为
选出2人使用版本相同的方法数为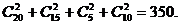
故2人使用版本相同的概率为: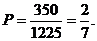 …………………………6分
…………………………6分
(2)∵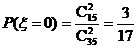 ,
,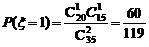
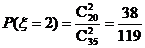
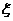 |
0 |
1 |
2 |
|
P |
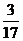 |
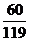 |
 |
∴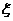 的分布列为
的分布列为
………………10分
∴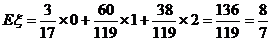 ……………………12分
……………………12分
19.解:法一 :以A点为原点,AB为x轴,AD为y轴,AD为z轴的空间直角坐标系,
则依题意可知相关各点的坐标分别是A(0,0,0),B(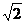 ,0,0),C(
,0,0),C(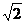 ,1,0),
,1,0),
D(0,1,0),S(0,0,1)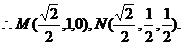 ……………………2分
……………………2分
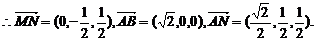 …………………………4分
…………………………4分
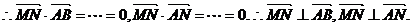
∴MN⊥平面ABN.……………………………………………………………………6分
(2)设平面NBC的法向量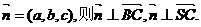 且又易知
且又易知
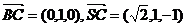
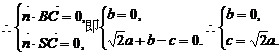
令a=1,则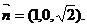 …………………………………………………………9分
…………………………………………………………9分
显然,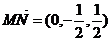 就是平面ABN的法向量.
就是平面ABN的法向量.
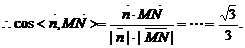 ………………………………………10分
………………………………………10分
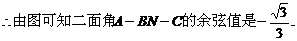 ………………………………………12分
………………………………………12分
法二:(1)由题意知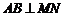 连
连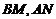 则可求
则可求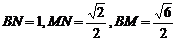 ,则
,则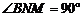
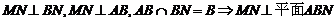 …………………………6分
…………………………6分
(2)因为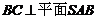 ,在平面
,在平面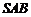 内作
内作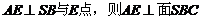 且
且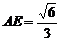 ,
,
又在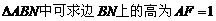 ,所以
,所以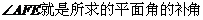 ,
,
且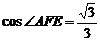 故所求的二面角的余弦值为
故所求的二面角的余弦值为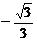 ………………………12分
………………………12分
18. 解:设
解:设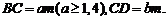 连结BD.
连结BD.
则在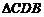 中,
中,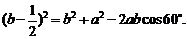
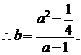
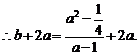 ………………………………6分
………………………………6分
设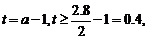
则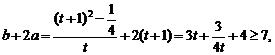 ………………………………10分
………………………………10分
等号成立时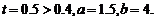 ……………………………………………11分
……………………………………………11分
答:当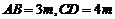 时,建造这个支架的成本最低. ……………………12分
时,建造这个支架的成本最低. ……………………12分
13:3 14: 120 15: 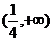 16: ③④
16: ③④
1--5 C A D A D 6--10 A D A C B 11 C 12 C
22.已知函数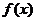 与
与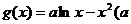 为常数)的图象关于直线x=1对称,
为常数)的图象关于直线x=1对称,
且x=1是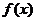 的一个极值点.
的一个极值点.
(1)求出函数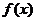 的表达式和单调区间;
的表达式和单调区间;
(2)若已知当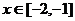 时,不等式
时,不等式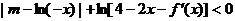 恒成立,
恒成立,
求m的取值范围.
高三9月份月考数学试卷答案及评分标准
21.已知椭圆C: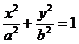 (a>b>0)的离心率为
(a>b>0)的离心率为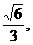 短轴一个端点到右焦点的
短轴一个端点到右焦点的
距离为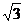 .
.
(Ⅰ)求椭圆C的方程;
(Ⅱ)设直线l与椭圆C交于A、B两点,坐标原点O到直线l的距离为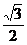 ,求△AOB面积的最大值.
,求△AOB面积的最大值.
20.某研究机构准备举行一次数学新课程研讨会,共邀请50名一线教师参加,使用不同版本教材的教师人数如下表所示:
|
版本 |
人教A版 |
人教B版 |
苏教版 |
北师大版 |
|
人数 |
20 |
15 |
5 |
10 |

(1)从这50名教师中随机选出2名,求2人所使用版本相同的概率;
(2)若随机选出2名使用人教版的教师发言,设使用人教A版的教师人数为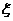 ,求随机变量
,求随机变量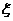 的分布列和数学期望。
的分布列和数学期望。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com