4．解决匀速圆周运动问题的方法

①明确质点匀速圆周运动的圆心和半径；

②寻找各物理量之间的联系，灵活选取公式进行计算；

③运用两个重要的结论：同一转盘上各点的角速度相同，同一皮带轮缘上各点的线速度大小相等。

④注意匀速圆周运动的周期性引起的多解问题。

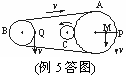
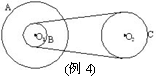例4　 如图所示的皮带传动装置，主动轮O₁上两轮的半径分别为3r和r，从动轮O₂的半径为2r，A、B、C分别为轮缘上的三点，设皮带不打滑，求：

⑴ A、B、C三点的角速度之比ω_A∶ω_B∶ω_C=　　　

⑵ A、B、C三点的线速度大小之比v _A∶v_B∶v_C=　　　

解析 　皮带不打滑，表示皮带接触点处线速度大小相等，故v_B=v_C.，因A与B为同一轮上两点，角速度相等，线速度与半径成正比，v_A=3v_B，故三点线速度之比为3∶1∶1

因v_B=v_C，当线速度相等时，角速度与半径成反比，r_B∶r_C=1∶2，所以ω_B∶ω_C=2∶1，又ω_A=ω_B，故三点角速度之比为2∶2∶1。答案：2∶2∶1 ，3∶1∶1

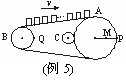例5　 如图所示是生产流水线上的皮带传输装置，传输带上等间距地放着很多半成品产品。A轮处装有光电计数器，它可以记录通过A处的产品数目。已知测得轮A、B的半径分别为r_A=20 cm，r_B=10 cm，相邻两产品距离为30 cm，1 min内有41个产品通过A处。求：

(1) 产品随传输带移动的速度大小；

(2) A、B轮轮缘上的两点P、Q及A轮半径中点M的线速度和角速度大小，并在图中画出线速度方向；

(3) 如果A轮是通过摩擦带动C轮转动，且r_C=5 cm，在图中描出C轮的转动方向，求出C轮的角速度(假设轮不打滑)。

解析 　首先明确产品与传送带保持相对静止的条件下，产品速度的大小就等于传送带上每一点速度的大小，在传送带不打滑的条件下，传送带上各点运动速度的大小都等于A、B轮缘上点的线速度的大小。由传送带相邻产品的间距及单位时间内通过A处的产品的个数可以确定出皮带上点的速度，进而知道A、B轮缘上的两点P、Q线速度的大小，然后由线速度与角速度的关系，求出A、B两轮的角速度及A轮半径中点M的线速度及C轮的角速度。由题意知，1分钟内有41个产品通过A处，说明1分钟内传输带上每点运动的路程为两产品间距的40倍。设传输带运动速度大小为v，则

(1)v=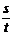=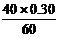m/s=0.2 m/s

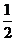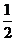(2)v_P=v_Q=0.2 m/s ，.A轮半径上的M点与P点的角速度相等，故v_M=v_P=×0.2 m/s=0.1 m/s

ω_P=ω_M=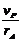=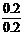rad/s=1 rad/s ，ω_Q=2ω_P=2 rad/s

　(3)C轮的转动方向如图所示，如果两轮间不打滑，则它们的接触处是相对静止的，即它们轮缘的线速度大小是相等的，所以ω_Cr_C=ω_Ar_A

C轮的角速度ω_C=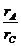ω_A=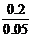×1 rad/s=4 rad/s

答案　 (1)0.2 m/s　 (2)v_P=v_Q=0.2 m/s ，v_M =0.1 m/s ，ω_P=ω_M =1 rad/s　 ω_Q=2 rad/s　 (3)ω_C=4 rad/s

点评　 本题旨在考查学生对传动装置中各物理量的联系的理解，并能熟练地运用匀速圆周运动的规律解决问题。

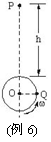
例6 　如图所示，小球Q在竖直平面内做匀速圆周运动，当Q球转到图示位置时，有另一小球P在距圆周最高点为h处开始自由下落，要使两球在圆周最高点相碰，则Q球的角速度ω应满足什么条件？

解析　 设P球自由落体到圆周最高点的时间为t，由自由落体可得

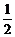gt²=h　　 求得t=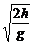

Q球由图示位置转至最高点的时间也是t，但做匀速圆周运动，周期为T，有

t = (4n+1)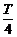　 (n=0，1，2，3……)

两式联立再由T=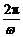得　 (4n+1)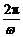=　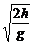　　 所以ω=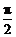(4n+1)　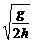 (n=0，1，2，3……)

答案　 ω = 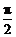(4n+1)　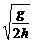 ， (n=0，1，2，3……)

点评　 在这类题目中“时间”是联系不同运动的桥梁，且往往这类题目由于匀速圆周运动的周期性给结果带来多解性，使求得的结果为通解。

[同步检测]

3．描写圆周运动的各物理量之间的关系

(1)线速度与角速度的关系

在v=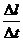中取△t=T(1个周期的时间)，则△l=2πr，所以v=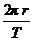；在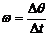中，取△t=T，则△θ=2π，所以ω=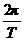，比较可见v=ωr，这个重要的关系也可以由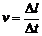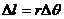，推出，即v=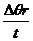=ωr。这个关系的意义是线速度的大小等于角速度与半径的乘积。

　(2)角速度、周期、频率、转速间的关系

ω=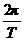=2πf=2πn (n为r/s)。

2．匀速圆周运动

(1)定义：物体沿着圆周运动，并且线速度大小处处相等的运动。

(2)特点：线速度的大小恒定，角速度、周期和频率都是恒定不变的。

(3)性质：是速度大小不变而速度方向时刻在变的变速曲线运动。

例3　 对于做匀速圆周运动的物体，下列说法正确的是(　　 )

A．相等的时间里通过的路程相等

B．相等的时间里通过的弧长相等

C．相等的时间里发生的位移相同

D．相等的时间里转过的角度相等

解析　 质点做匀速圆周运动时，因线速度的大小不变，故在相等的时间内通过的圆弧长度相等，即路程相等，A、B项正确，因角速度相等，此时半径转过的角度也相等，D项正确，但由于位移是矢量，在相等时间里，质点的位移大小相等，方向却不一定相同，因此位移不一定相同，故C项错误。本题选ABD

1．描述圆周运动的物理量

(1) 线速度

①定义：质点沿圆周运动通过的弧长Δl与所需时间Δt的比值叫做线速度。

②物理意义：描述质点沿圆周运动的快慢．

③大小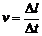：(m/s)

　 如果Δt取得很小，v就为瞬时线速度，此时Δl的方向就与半径垂直，即沿该点的切线方向。

④方向：质点在圆周上某点的线速度方向沿圆周上该点的切线方向。

(2) 角速度

①定义：在圆周运动中，连接运动质点和圆心的半径转过的角度Δθ与所用时间Δt的比值，就是质点运动的角速度。

②物理意义：描述质点绕圆心转动的快慢．

③大小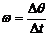： 　(单位为弧度/秒，符号是rad／s)

(3) 周期T，频率f和转速n

做圆周运动的物体运动一周所用的时间叫周期，用T表示，单位为秒(s)。

做圆周运动物体在1秒内沿圆周绕圆心转过的圈数叫做频率，用f表示，单位为赫兹(Hz)。

做圆周运动物体在单位时间内沿圆周绕圆心转过的圈数叫做转速，用n表示，单位为转每秒(r/s)或转每分(r/min)。显然，当单位时间取1 s时，f = n。

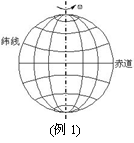
例1　 如图所示，静止在地球上的物体都要随地球一起转动，下列说法正确的是(　　 )

A．它们的运动周期都是相同的

B．它们的线速度都是相同的

C．它们的线速度大小都是相同的

D．它们的角速度是不同的

解析　 地球绕自转轴转动时，所有地球上各点的周期及角速度都是相同的，地球表面物体做圆周运动的平面是物体所在纬度线平面，其圆心分布在整条自转轴上。不同纬度处物体做圆周运动的半径是不同的，只有同一纬度处的物体转动半径相等，线速度的大小才相等，但即使物体的线速度大小相同，方向也各不相同。答案：A

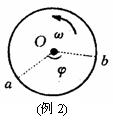例2　 如图所示，直径为d的纸质圆筒，以角速度ω绕轴O高速运动，有一颗子弹沿直径穿过圆筒，若子弹穿过圆筒时间小于半个周期，在筒上先、后留下a、b两个弹孔，已知ao、bo间夹角为φ弧度，则子弹速度为 　　　　　　

解析 子弹在a处进入筒后，沿直径匀速直线运动，经t=d/v时间打在圆筒上，在t时间内，圆筒转过的角度θ＝ωt=π－φ，则d/v=(π－φ)/ω，v=dω/(π－φ)

答案 　dω/(π－φ)

3．在数学中，可以用“弧度”来表示角的大小，它等于　　　　　　 的比值。

[同步导学]

2．曲线运动中，质点在某一点的速度方向是　　　　　　　　　　　　　　 　　　　 ，曲线运动中速度的方向时刻在变，所以曲线运动是　　　。

1．直线运动中，速度等于　　　　　　　　　　　　　　　　　 的比值，公式是　　　 。