
12.(2010双基测试)
已知椭圆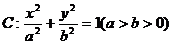 经过点
经过点 ,且两焦点与短轴的一个端点构成等腰直角三角形。
,且两焦点与短轴的一个端点构成等腰直角三角形。
(1)求椭圆的方程;
(2)动直线 交椭圆C于A、B两点,试问:在坐标平面上是否存在一个定点T,使得以AB为直径的圆恒过点T。若存在,求出点T的坐标;若不存在,请说明理由。
交椭圆C于A、B两点,试问:在坐标平面上是否存在一个定点T,使得以AB为直径的圆恒过点T。若存在,求出点T的坐标;若不存在,请说明理由。
2010年新课标省市高三数学模拟题分类
第五节 平面解析几何(圆锥曲线)详解答案
11.(2010全国四校二模)
如图,S(1,1)是抛物线为 上的一点,弦SC,SD分别交
上的一点,弦SC,SD分别交 小轴于A,B两点,且SA=SB。
小轴于A,B两点,且SA=SB。
(I)求证:直线CD的斜率为定值;
(Ⅱ)延长DC交 轴于点E,若
轴于点E,若 ,求
,求 的值。
的值。

10.(2010重点中学协作体三模)
椭圆 的左、右焦点为F1、F2,过F1的直线l与椭圆交于A、B两点.
的左、右焦点为F1、F2,过F1的直线l与椭圆交于A、B两点.
(1)如果点A在圆 (c为椭圆的半焦距)上,且|F1A|=c,求椭圆的离心率;
(c为椭圆的半焦距)上,且|F1A|=c,求椭圆的离心率;
(2)若函数 的图象,无论m为何值时恒过定点
的图象,无论m为何值时恒过定点 ,求
,求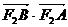 的取值范围.
的取值范围.
9.(2010浙江省高考预测)
点M在椭圆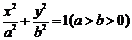 上,以M为圆心的圆与x轴相切于椭圆的右焦点F.
上,以M为圆心的圆与x轴相切于椭圆的右焦点F.
(I)若圆M与y轴相交于A、B两点,且△ABM是边长为2的正三角形,求椭圆的方程;
(II)已知点F(1,0),设过点F的直线l交椭圆于C、D两点,若直线l绕点F任意转动时,恒有 成立,求实数
成立,求实数 的取值范围.
的取值范围.
8.(2010宁夏高考调研)
已知椭圆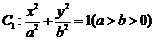 的离心率为
的离心率为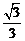 ,直线
,直线 与以原点为圆心,椭圆
与以原点为圆心,椭圆 的短半轴长为半径的圆相切.
的短半轴长为半径的圆相切.
(I)求椭圆 的方程;
的方程;
(II)直线 过椭圆
过椭圆 的左焦点
的左焦点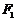 ,且与
,且与 轴垂直,动直线
轴垂直,动直线 垂直于直线
垂直于直线 ,垂足为点
,垂足为点 ,线段
,线段 的垂直平分线交
的垂直平分线交 于点
于点 ,求点
,求点 的轨迹
的轨迹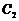 的方程;
的方程;
(III)设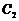 上的两个不同点
上的两个不同点 、
、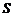 满足
满足 ,求
,求 的取值范围(
的取值范围(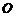 为坐标原点).
为坐标原点).
7.(2010东北三校一模)
如图,设抛物线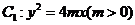 的准线与
的准线与 轴交于
轴交于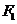 ,焦点为
,焦点为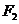 ;以
;以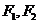 为焦点,离心率
为焦点,离心率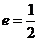 的椭圆
的椭圆 与抛物线
与抛物线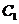 在
在 轴上方的交点为
轴上方的交点为 ,延长
,延长 交抛物线于点
交抛物线于点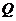 ,
,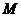 是抛物线
是抛物线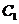 上一动点,且M在
上一动点,且M在 与
与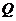 之间运动.
之间运动.
(1)当 时,求椭圆
时,求椭圆 的方程;
的方程;
 (2)当
(2)当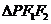 的边长恰好是三个连续的自然数时,求
的边长恰好是三个连续的自然数时,求 面积的最大值.
面积的最大值.
6.(2010北京石景山模拟)
已知椭圆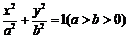 的离心率为
的离心率为 ,短轴的一个端点到右焦点的距离为
,短轴的一个端点到右焦点的距离为 ,直线
,直线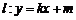 交椭圆于不同的两点
交椭圆于不同的两点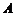 ,
, .
.
⑴求椭圆的方程;
⑵若 ,且
,且 ,求
,求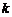 的值(
的值(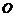 点为坐标原点);
点为坐标原点);
⑶若坐标原点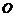 到直线
到直线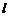 的距离为
的距离为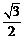 ,求
,求 面积的最大值.
面积的最大值.
5.(2010吉林实验中学第八次模拟)
已知中心在原点,焦点在 轴上的椭圆C的离心率为
轴上的椭圆C的离心率为 ,且经过点
,且经过点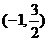 ,过点P(2,1)的直线
,过点P(2,1)的直线 与椭圆C在第一象限相切于点M .
与椭圆C在第一象限相切于点M .
(1)求椭圆C的方程;
(2)求直线 的方程以及点M的坐标;
的方程以及点M的坐标;
(3) 是否存过点P的直线 与椭圆C相交于不同的两点A、B,满足
与椭圆C相交于不同的两点A、B,满足 ?若存在,求出直线l1的方程;若不存在,请说明理由.
?若存在,求出直线l1的方程;若不存在,请说明理由.
4.(2010辽宁丹东二模)
已知抛物线 的焦点为F,椭圆C:
的焦点为F,椭圆C: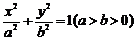 的离心率为
的离心率为 ,
, 是它们的一个交点,且
是它们的一个交点,且 .
.
(I)求椭圆C的方程;
(II)若直线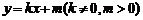 与椭圆C交于两点A、B,点D满足
与椭圆C交于两点A、B,点D满足 =0,直线FD的斜率为
=0,直线FD的斜率为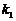 ,试证明
,试证明 .
.
3.(2010北京海淀区一模)
已知椭圆 的中心在原点,焦点在
的中心在原点,焦点在 轴上,左右焦点分别为
轴上,左右焦点分别为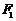 ,
,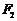 ,且
,且 ,点
,点 在椭圆
在椭圆 上.
上.
⑴求椭圆 的方程;
的方程;
⑵过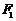 的直线
的直线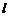 与椭圆
与椭圆 相交于
相交于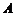 、
、 两点,且
两点,且 的面积为
的面积为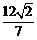 ,求以
,求以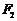 为圆心且与直线
为圆心且与直线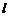 相切的圆的方程.
相切的圆的方程.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com