
2、(07全国Ⅰ)设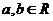 ,集合
,集合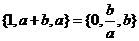 ,则
,则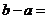 ( )
( )
A、1
B、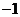 C、2
D、
C、2
D、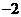
1、(07广东)已知函数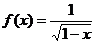 的定义域为
的定义域为 ,
,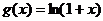 的定义域为
的定义域为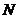 ,则
,则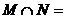 ( )A、
( )A、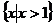 B、
B、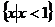 C、
C、 D、
D、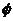
4、(04山西)设集合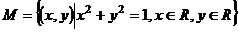 ,
,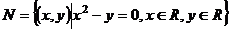 ,则集合
,则集合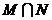 中元素的个数为( )
中元素的个数为( )
A、1 B、2 C、3 D、4
3、(06辽宁)设集合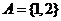 ,则满足
,则满足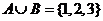 的集合
的集合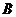 的个数是( )
的个数是( )
A、1 B、3 C、4 D、8
2、(06山东)定义集合运算:A⊙B={z︳z= xy(x+y),z∈A,y∈B},设集合A={0,1},B={2,3},则集合A⊙B的所有元素之和为( )
A、0 B、6 C、12 D、18
1、(07山东)已知集合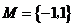 ,
,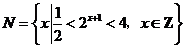 ,则
,则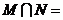 ( )
( )
A.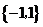 B.
B.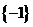 C.
C.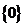 D.
D.
(三)解答题:
10、(07陕西20)设函数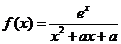 ,其中
,其中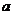 为实数.(I)若
为实数.(I)若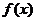 的定义域为
的定义域为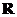 ,求
,求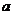 的取值范围;(II)当
的取值范围;(II)当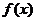 的定义域为
的定义域为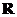 时,求
时,求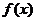 的单调减区间
的单调减区间
11、(06山东)设函数f(x)=ax-(a+1)ln(x+1),其中a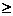 -1,求f(x)的单调区间。
-1,求f(x)的单调区间。
12、(04山东)已知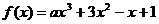 在R上是减函数,求
在R上是减函数,求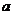 的取值范围。
的取值范围。
(二)填空题:
8、(07海南14)设函数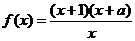 为奇函数,则
为奇函数,则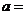 ;
;
9、(06海南、全国Ⅰ)设函数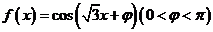 。若
。若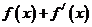 是奇函数,则
是奇函数,则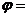 __________。
__________。
(一)选择题:
1、(07福建) 已知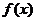 为
为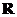 上的减函数,则满足
上的减函数,则满足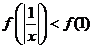 的实数
的实数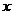 的取值范围是( )
的取值范围是( )
A、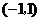 B、
B、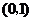 C、
C、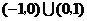 D、
D、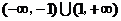
2、(07北京) 对于函数①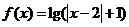 ,②
,②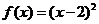 ,③
,③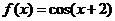 ,判断如下三个命题的真假:
,判断如下三个命题的真假:
命题甲: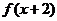 是偶函数;
是偶函数;
命题乙: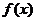 在
在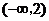 上是减函数,在
上是减函数,在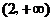 上是增函数;
上是增函数;
命题丙: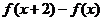 在
在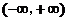 上是增函数.
上是增函数.
能使命题甲、乙、丙均为真的所有函数的序号是( )
A、①③ B、①② C、③ D、②
3、(07江苏) 设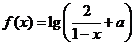 是奇函数,则使
是奇函数,则使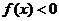 的
的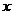 的取值范围是( )
的取值范围是( )
A、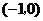 B、
B、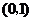 C、
C、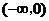 D、
D、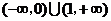
4、(07)重庆已知定义域为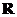 的函数
的函数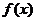 在
在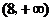 上为减函数,且函数
上为减函数,且函数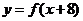 为偶函数,则( )
为偶函数,则( )
A、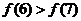 B、
B、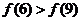 C、
C、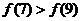 D、
D、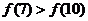
5、(07安徽) 定义在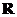 上的函数
上的函数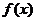 既是奇函数,又是周期函数,
既是奇函数,又是周期函数,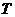 是它的一个正周期.若将方程
是它的一个正周期.若将方程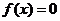 在闭区间
在闭区间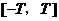 上的根的个数记为
上的根的个数记为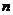 ,则
,则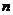 可能为( )
可能为( )
A、0 B、1 C、3 D、5
6、(06山东) 已知定义在R上的奇函数f(x)满足f(x+2)=-f(x),则,f(6)的值为
A、-1 B、0 C、 1 D、2
7、(06全国Ⅱ) 函数y=f(x)的图像与函数g(x)=log2x(x>0)的图像关于原点
对称,则f(x)的表达式为
A、f(x)=(x>0) B、f(x)=log2(-x)(x<0)
C、f(x)=-log2x(x>0) D、f(x)=-log2(-x)(x<0)
例1、(07天津) 在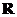 上定义的函数
上定义的函数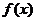 是偶函数,且
是偶函数,且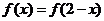 ,若
,若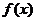 在区间
在区间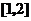 上是减函数,则
上是减函数,则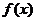 ( )
( )
A.在区间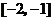 上是增函数,在区间
上是增函数,在区间 上是增函数
上是增函数
B.在区间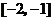 上是增函数,在区间
上是增函数,在区间 上是减函数
上是减函数
C.在区间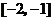 上是减函数,在区间
上是减函数,在区间 上是增函数
上是增函数
D.在区间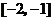 上是减函数,在区间
上是减函数,在区间 上是减函数
上是减函数
例2、(06北京)已知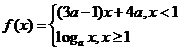 是
是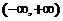 上的增函数,那么
上的增函数,那么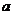 的取值范围是 ( )
的取值范围是 ( )
A、(0,1) B、(0,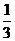 ) C、
) C、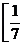 ,
,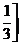 D、
D、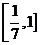
例3、(06福建21)已知函数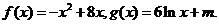 (I)求
(I)求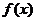 在区间
在区间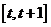 上的最大值
上的最大值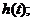 (II)是否存在实数
(II)是否存在实数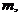 使得
使得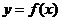 的图象与
的图象与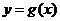 的图象有且只有三个不同的交点?若存在,求出
的图象有且只有三个不同的交点?若存在,求出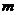 的取值范围;若不存在,说明理由。
的取值范围;若不存在,说明理由。
解:(I)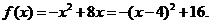
当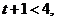 即
即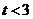 时,
时,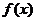 在
在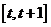 上单调递增,
上单调递增,
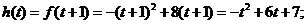
当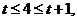 即
即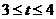 时,
时,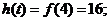
当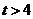 时,
时,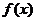 在
在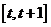 上单调递减,
上单调递减,
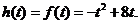
综上,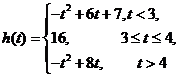
(II)函数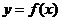 的图象与
的图象与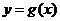 的图象有且只有三个不同的交点,即函数
的图象有且只有三个不同的交点,即函数
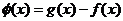 的图象与
的图象与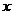 轴的正半轴有且只有三个不同的交点。
轴的正半轴有且只有三个不同的交点。
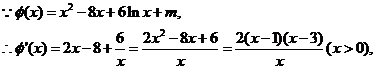
当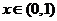 时,
时,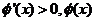 是增函数;
是增函数;
当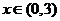 时,
时,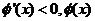 是减函数;
是减函数;
当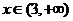 时,
时,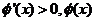 是增函数;
是增函数;
当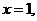 或
或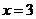 时,
时,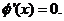
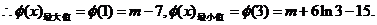
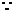 当
当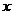 充分接近0时,
充分接近0时,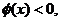 当
当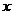 充分大时,
充分大时,
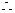 要使
要使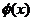 的图象与
的图象与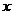 轴正半轴有三个不同的交点,必须且只须
轴正半轴有三个不同的交点,必须且只须
 即
即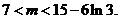
所以存在实数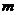 ,使得函数
,使得函数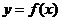 与
与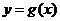 的图象有且只有三个不同的交点,
的图象有且只有三个不同的交点,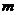 的取值范围为
的取值范围为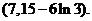
例4、(05天津16)设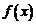 是定义在R上的奇函数,且
是定义在R上的奇函数,且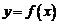 的图象关于直线
的图象关于直线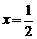 对称,则
对称,则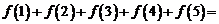 __________;
__________;
例5、(05广东19)设函数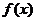 在
在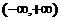 上满足
上满足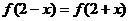 ,
,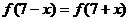 ,且在闭区间[0,7]上,只有
,且在闭区间[0,7]上,只有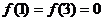 .
.
(Ⅰ)试判断函数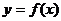 的奇偶性;
的奇偶性;
(Ⅱ)试求方程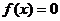 在闭区间
在闭区间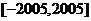 上的根的个数,并证明你的结论.
上的根的个数,并证明你的结论.
[答案]
解:(Ⅰ)∵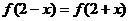 ,
,
∴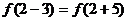
即 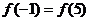 ,
,
∵在[0,7]上,只有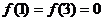 ,
,
∴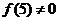 ,∴
,∴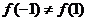 ,
,
∴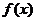 是非奇非偶函数.
是非奇非偶函数.
(Ⅱ)由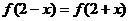 ,令
,令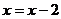 ,得
,得 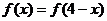 ,
,
由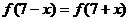 ,令
,令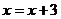 ,得
,得 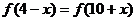 ,
,
∴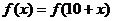 ,
,
∴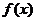 是以10为周期的周期函数,
是以10为周期的周期函数,
由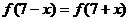 得,
得,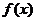 的图象关于
的图象关于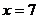 对称,
对称,
∴在[0,11]上,只有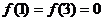 ,
,
∴10是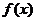 的最小正周期,
的最小正周期,
∵在[0,10]上,只有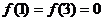 ,
,
∴在每一个最小正周期内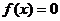 只有两个根,
只有两个根,
∴在闭区间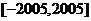 上的根的个数是
上的根的个数是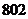 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com