
同步练习 9.5空间的角和距离
1.正方体ABCD-A1B1C1D1的棱长为a,E是CC1的中点,则E到A1B的距离是 ( )
A. 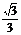 a B.
a B. 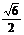 a C.
a C. 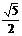 a D.
a D. 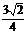 a
a
[例1]如图,三棱锥D-ABC中,平面ABD、平面ABC均为等腰直角三角形,∠ABC=∠BAD=900,其腰BC=a,且二面角D-AB-C=600.
(1) 求异面直线DA与BC所成的角;
(2) 求异面直线BD与AC所成的角;
(3) 求D到BC的距离;
(4) 求异面直线BD与AC的距离.
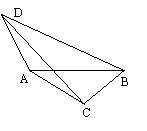
解析:(1)DA与BC成600角
(2)设BE中点为O,DE中点为F,连OF,则OF//BD,求∠AOF即为
异面直线BD与AC成角在ΔAOF中可求得∠AOF
=arccos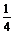
(3)∵ BA⊥平面ADE ∴ 平面DAE⊥平面ABC故取AE中点M,则有DM⊥平面ABC;取BC中点N,由MN⊥BC,根据三垂线定理,DN⊥BC ∴ DN是D到BC的距离
在△DMN中,DM=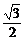 a,MN=a ∴ DN=
a,MN=a ∴ DN=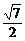 a
a
(4)∵ BF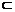 平面BDF,AC
平面BDF,AC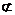 平面BDF,AC∥BF
平面BDF,AC∥BF
∴ AC∥平面BDF;
又BD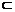 平面BDF
平面BDF
∴ AC与BD的距离即AC到平面BDF的距离
∵ 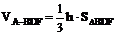 ,
,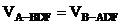
∴ 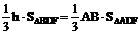

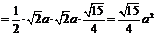
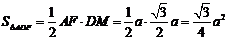
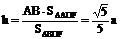 ,
,
即异面直线BD与AC的距离为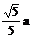
◆评注:三棱锥的等体积变换求高,也是求点到面距离的常用方法.
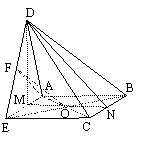
[例2](2006邯郸二模)如图,在四棱锥P-ABCD中,底面ABCD是直角梯形,AB⊥AD,AB∥DC,AB=4,AD=DC=2,侧面PAD是正三角形,且与底面垂直,M是PB的中点,
(Ⅰ) 求证:CM∥侧面PAD;
(Ⅱ)求直线CM与底面ABCD所成的角;
(Ⅲ)求侧面PBC与侧面PAD所成二面角的大小
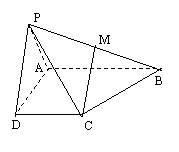

解:(Ⅰ)证明:作MN∥AB交AP于N,连结DN,
则MN∥AB∥CD,且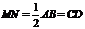
∴CM∥ND,CM∥平面PAD
(Ⅱ)∵CM∥ND, ∴ND与平面ABCD所成的角为所求.
∵侧面PAD⊥底面ABCD,∴ND在平面ABCD上的射影为AD
∴∠AND为所求; ∵⊿PAD是正三角形,N是PA的中点
∴CM与底面所成的角为30º.
(Ⅲ)延长AD、BC交于点E,连结P、E.
则PE为所求二面角的棱,且AD=DE=PD
所以,∠APE=90º,AP⊥PE
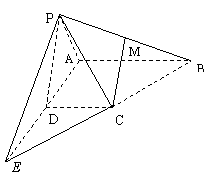
又∵AB⊥AD,平面PAD⊥底面ABCD
∴AB⊥平面PAE
∴BP⊥PE, ∠BPA为所求二面角的平面角
tan∠BPA=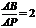
所以,侧面PBC与侧面PAD所的角为arctan2
[例3]如图,已知二面角α-PQ-β为60°,点A和点B分别在平面α和平面 β 内,点C在棱PQ上,∠ACP=∠BCP=30°,CA=CB=a.
(1)求证:AB⊥PQ;
(2)求点B到平面α的距离;
(3)设R是线段CA上的一点,直线BR与平面α所成的角为45°,求线段CR的长度.
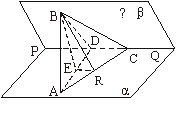

证明(1):在平面β内作BD⊥PQ于D,连结AD.
∵∠ACP=∠BCP=30°,CA=CB=a,CD公用,
∴△ACD≌△BCD . ∴∠ADC=∠BDC= 90°,即AD⊥PQ.于是PQ⊥平面ABD,
则AB⊥PQ.
(2)解:由(1)知,∠ADB是二面角α-PQ-β的平面角,
∴∠ADB=60°.又PQ⊥平面ABD,
∴α⊥平面ABD.过B作BE⊥AD于点E,则BE即为B到平面α的距离.
BE=BD·sin60°=BC·sin30°·sin60°=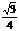 a.
a.
(3) 解:连结ER,∵BE⊥α,∴∠BRE是BR与α所成的角,
即∠BRE=45°,则有BR= =
= a.易知△ABD为正三角形,AB=AD=BD=
a.易知△ABD为正三角形,AB=AD=BD=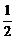 a.
a.
在△ABC中,由余弦定理得cos∠BCA=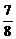 .
.
在△BCR中,设CR=x,由余弦定理得( a)2=x2+a2-2ax·
a)2=x2+a2-2ax·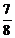 ,求得x1=
,求得x1= ,x2=
,x2=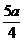 (舍去,∵CR<AC=a),故CR=
(舍去,∵CR<AC=a),故CR= .
.
[例4]四棱锥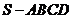 中,底面ABCD为平行四边形,侧面
中,底面ABCD为平行四边形,侧面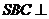 底面ABCD,已知
底面ABCD,已知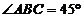 ,
,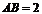 ,
,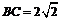 ,
, .
.
(Ⅰ)证明: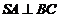 ;
;
(Ⅱ)求直线SD与平面SBC所成角的大小.
解:(1)作 ,垂足为
,垂足为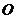 ,连结
,连结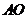 ,由侧面
,由侧面 底面
底面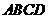 ,得
,得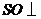 底面
底面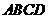 .
.
因为 ,所以
,所以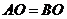 ,
,
又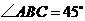 ,故
,故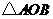 为等腰直角三角形,
为等腰直角三角形,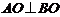 ,由三垂线定理,得
,由三垂线定理,得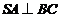 .
.
(Ⅱ)由(Ⅰ)知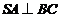 ,依题设
,依题设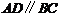 ,
,


故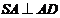 ,由
,由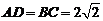 ,
,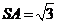 ,
,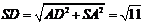 .
.
又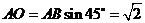 ,作
,作 ,垂足为
,垂足为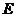 ,则
,则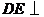 平面
平面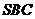 ,连结
,连结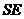 .
.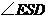 为直线
为直线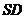 与平面
与平面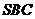 所成的角.
所成的角.
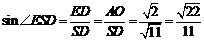
∴直线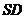 与平面SBC所成的角为
与平面SBC所成的角为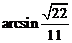 .
.
5.“如果两个二面角的两个半平面分别对应垂直,那麽这两个二面角的平面角相等或互补”.当两棱不平行不成立,所以,这个命题是错误的. 6。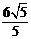
3.提示:四个面全等,设面积为S,设三个侧面在底面上的射影分别是S1、S2、S3,则 S= S1+S2+S3=Scosα+Scosβ+Scosγ…
2.提示:作PO⊥平面ABC于O,则O是Δ的外接圆圆心,且∠AOB=1200……
6。正三棱锥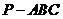 的高为
的高为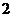 ,侧棱与底面
,侧棱与底面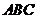 成
成 角,则点
角,则点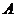 到侧面
到侧面 的距离为_____.
的距离为_____.
◆答案提示:1-3.ABA; 4.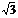
 ;
;
5.对于平面几何中的命题“如果两个角的两边分别对应垂直,那么这两个角相等或互补”,在立体几何中,类比上述命题可以得到命题__________,这个命题的真假性是______ .
4.设PA⊥Rt△ABC所在的平面α,∠BAC=90°,PB、PC分别与α成45°和30°角,PA=2,则PA与BC的距离是_____________;点P到BC的距离是_____________.
3.三棱锥V-ABC中,VA=BC,VB=AC,VC=AB,侧面与底面ABC所成二面角分别为α,β,γ(都是锐角),则cosα+cosβ+cosγ等于 ( )
A.1 B.2
C.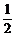 D.
D.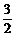
2.在△ABC中,AB=15,∠BCA=120°,若△ABC所在平面α外一点P到A、B、C的距离都是14,则P到α的距离是 ( )
A.13 B.11 C.9 D.7
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com