
2.在△ABC中,∠A>∠B是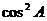 <
<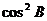 的 ( )
的 ( )
A.充分必要条件 B.必要不充分条件
C.充分不必要条件 D.既不充分也不必要条件
例1中利用三角形面积公式与余弦定理找出了角C得关系式,求出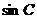 的值是关键。例2和例3综合运用了三角函数余弦定理等知识解决问题。有利于培养学生的运算能力和对知识的整合能力。
的值是关键。例2和例3综合运用了三角函数余弦定理等知识解决问题。有利于培养学生的运算能力和对知识的整合能力。
备用题:在△ABC中,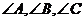 所对的边分别为
所对的边分别为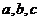 且
且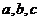 依次成等比数列,求
依次成等比数列,求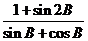 的取值范围
的取值范围
冲 刺 强 化 训 练(9)
1.在△ABC中,∠A= ,b=1,△ABC的面积为
,b=1,△ABC的面积为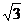 ,则△ABC的外接圆的直径为 ( )
,则△ABC的外接圆的直径为 ( )
A.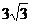 B.
B.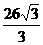 C.
C.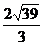 D.
D.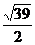
例1.△ABC的三边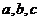 和面积
和面积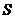 满足关系
满足关系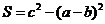 ,且
,且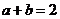 ,求面积
,求面积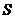

的最大值。











例2.平面上有四点A、B、Q、P,其中A、B为定点,且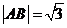 , P、Q为动点,满足
, P、Q为动点,满足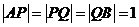 ,⊿APB和⊿PQB的面积分别为
,⊿APB和⊿PQB的面积分别为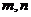 。
。
(1)求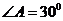 ,求
,求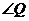

(2) 求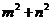 的最大值
的最大值
例3.△ABC的三个内角A,B,C成等差数列,他们所对的边分别为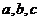 ,若
,若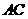 边上的高
边上的高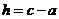 。求
。求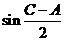 的值
的值
5.在直角△ABC中,两锐角为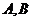 ,则
,则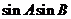 ( )
( )
A. 有最大值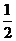 ,最小值0
B. 有最大值
,最小值0
B. 有最大值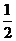 ,无最小值
,无最小值
C. 无最大值,无最小值 D.
有最大值1,也有最小值0
4.在△ABC中,若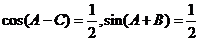 则三角形三内角满足 ( )
则三角形三内角满足 ( )
A.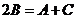 B.
B.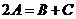 C.
C. 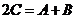 D.以上都不对
D.以上都不对
3. △ABC中,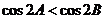 是
是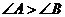 成立的
( )
成立的
( )
A.充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分也不必要条件
2.设A是△ABC的最小内角,那么函数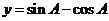 的值域是 ( )
的值域是 ( )
A.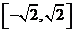 B.
B.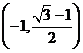 C.
C. 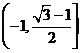 D.
D.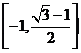

1.在△ABC中,若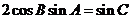 ,则△ABC的形状一定是 ( )
,则△ABC的形状一定是 ( )
A.等腰三角形B. 直角三角形C.等边三角形D. 等腰直角三角形
2.运用正、余弦定理及三角变换公式灵活进行边角转换
1.运用三角形内角和、正弦定理、余弦定理解斜三角形
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com