
(一)目标要求:
1. 识记要求:
(1)了解中国三大自然区的划分依据、界线、特点、成因。
(2)了解中国三大自然区内的差异表现及成因,更小的自然地区的划分依据及名称、各地区的特征。
2. 能力要求:
三大自然区内自然要素的相互关系
第一单元 中国的区域差异
1.1 我国的三大自然区 1.2 三大自然区的内部差异
同学们,本讲开始我们学习高中地理选修(二)的内容。选修(二)讲述的是有关国土整治的知识。全书以个案研究的方法,分析了我国国民经济发展中若干国土整治方面的典型案例。同学们在学习过程中,不仅要学习案例本身所讲述的地理事实及其原理,更重要的是通过个案,掌握分析问题的方法,做到能举一反三。学习中,要注意理论联系实际,关注国家经济生活中的大事和时事热点。用科学的观点去分析、评价它们的利弊得失。突出人类活动对地理环境的深刻影响。
本册教材的知识与初中地理的内容有着密切的联系。与初中地理的区别在于:它是以区域而不是以部门地理来组织教材的。它将部门地理的内容落实到具体区域上。所以说,本册教材涉及的许多知识都是以初中地理知识为基础的,是初中地理知识的提炼和综合。要学好本册教材所规定的内容,必须对初中地理知识进行复习和整理。
第一单元 中国的区域差异
在本书的第一单元首先从总体介绍我国的区域差异,帮助学生从整体把握我国国土的差异,为后面讲述我国国土的整治与开发专题提供背景知识。
本单元的内容分我国的自然差异和经济差异两方面。每一部分内容在讲述时,都是先大后小,先粗后细。如自然差异,先讲全国的三大自然区,然后再讲每一个自然区内部的差异;经济差异,先讲全国的三个经济地带,再讲每个地带的特征,重点分析东部地带的内部差异。
我国的自然差异这部分内容主要是帮助学生了解我国在自然环境方面存在的差异。综合地貌和气候这两个决定我国自然地理环境差异的因素,可把我国划分为东部季风区,西北干旱半干旱区和青藏高寒区三大自然区。每个自然区在地貌和气候方面都有明显的差别, 这种差别还间接反映在植被、土壤、水文等自然要素上,并且形成各区内部差异的主导因素也有所不同,最终对人类活动的影响也有明显差异。由此可见,三大自然区的划分不是仅依靠某一种自然要素的划分,而是一种综合性划分。这种综合划分能反映出自然区之间最大的差异。经济差异这部分内容主要从我国现阶段社会经济发展中存在的现状出发,讲述我国明显存在的地带性经济差异,并剖析这种差异产生的原因。通过这些内容的学习,有助于学生了解我国改革开放的发展过程,以及我国为合理利用各种资源、实现三个地带间协调发展所应采取的发展战略。
本单元共分4课。自然差异部分2课,经济差异部分2课。重点就是抓住差异性,从差异中寻找制约人地关系协调发展的因素,为后面各单元做好知识准备。
24.如图,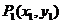 、
、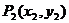 、…、
、…、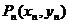
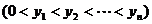 是曲线
是曲线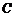 :
: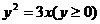 上的
上的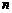 个点,点
个点,点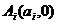 (
(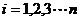 )在
)在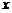 轴的正半轴上,且
轴的正半轴上,且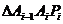 是正三角形(
是正三角形(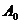 是坐标原点).
是坐标原点).
(1)写出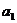 、
、 、
、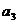 ;
;
(2)求出点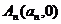 (
(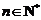 )的横坐标
)的横坐标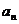 关于
关于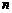 的表达式并证明.
的表达式并证明.
23. 中,已知
中,已知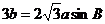 ,且
,且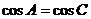 ,求证:
,求证: 为等边三角形。
为等边三角形。
22.已知a、b、c是互不相等的非零实数.若用反证法证明三个方程ax2+2bx+c=0,bx2+2cx+a=0,cx2+2ax+b=0至少有一个方程有两个相异实根.应假设
21.在△ABC中,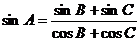 ,判断△ABC的形状并证明.
,判断△ABC的形状并证明.
20.如图的三角形数阵中,满足:(1)第1行的数为1;(2)第n(n≥2)行首尾两数均为n,其余的数都等于它肩上的两个数相加.则第n行(n≥2)中第2个数是________(用n表示).

19.已知△ABC三边a,b,c的长都是整数,且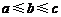 ,如果b=m(m
,如果b=m(m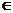 N*),则这样的三角形共有 个(用m表示).
N*),则这样的三角形共有 个(用m表示).
18、若数列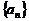 是等差数列,对于
是等差数列,对于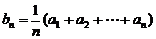 ,则数列
,则数列 也是等差数列。类比上述性质,若数列
也是等差数列。类比上述性质,若数列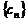 是各项都为正数的等比数列,对于
是各项都为正数的等比数列,对于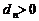 ,则
,则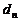 = 时,数列
= 时,数列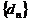 也是等比数列。
也是等比数列。
17.在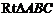 中,两直角边分别为
中,两直角边分别为 、
、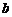 ,设
,设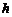 为斜边上的高,则
为斜边上的高,则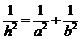 ,由此类比:三棱锥
,由此类比:三棱锥 中的三条侧棱
中的三条侧棱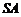 、
、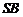 、
、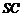 两两垂直,且长度分别为
两两垂直,且长度分别为 、
、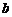 、
、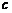 ,设棱锥底面
,设棱锥底面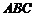 上的高为
上的高为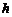 ,则
.
,则
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com