
1.A、B、C三球大小相同,A为实心木球,B为实心铁球,C是质量与A一样的空心铁球,三球同时从同一高度由静止落下,若受到的阻力相同,则( )
A.B球下落的加速度最大 B.C球下落的加速度最大
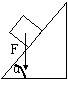 C.A球下落的加速度最大 D.B球落地时间最短,A、C球同落地
C.A球下落的加速度最大 D.B球落地时间最短,A、C球同落地
5.[解析]作出小球受力图如图(a)所示为绳子拉力F1与重力mg,不可能有沿斜面方向的合力,因此,小球与小车相对静止沿斜面做匀速运动,其加速度a1=0,绳子的拉力
F1=mg.
(2)作出小球受力图如图(b)所示,绳子的拉力F2与重力mg的合力沿斜面向下,小球的加速度a2=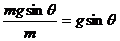 ,绳子拉力F2=mgcosθ
,绳子拉力F2=mgcosθ
(3)作出受力图如图(c)所示,小球的加速度 ,
,
绳子拉力 F3=mgcotθ
[答案](1)0,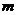 g (2)gsinθ,mgcosθ (3)g/sinθ mgcotθ
g (2)gsinθ,mgcosθ (3)g/sinθ mgcotθ
[能力训练]
5. 如图所示,一倾角为θ的斜面上放着一小车,小车上吊着小球m,小车在斜面上下滑时,小球与车相对静止共同运动,当悬线处于下列状态时,分别求出小车下滑的加速度及悬线的拉力。
如图所示,一倾角为θ的斜面上放着一小车,小车上吊着小球m,小车在斜面上下滑时,小球与车相对静止共同运动,当悬线处于下列状态时,分别求出小车下滑的加速度及悬线的拉力。
(1)悬线沿竖直方向。
(2)悬线与斜面方向垂直。
(3)悬线沿水平方向。
4. 以24.5m/s的速度沿水平面行驶的汽车上固定
以24.5m/s的速度沿水平面行驶的汽车上固定
一个光滑的斜面,如图所示,汽车刹车后,经2.5s
停下来,欲使在刹车过程中物体A与斜面保持相对
静止,则此斜面的倾角应为 ,车的行
驶方向应向 。(g取9.8m/s2)
3.重物A和小车B的重分别为GA和GB,用跨过定滑轮
|
 的细线将它们连接起来,如图所示。已知GA>GB,不计一切摩擦,则细线对小车B的拉力F的大小是( )
的细线将它们连接起来,如图所示。已知GA>GB,不计一切摩擦,则细线对小车B的拉力F的大小是( )
A.F=GA B.GA>F≥GB
C.F<GB D.GA、GB的大小未知,F不好确定
2. 一支架固定于放于水平地面上的小车上,细线上一端系着质量为m的小球,另一端系在支架上,当小车向左做直线运动时,细线与竖直方向的夹角为θ,此时放在小车上质量M的A物体跟小车相对静止,如图所示,则A受到的摩擦力大小和方向是(
)
一支架固定于放于水平地面上的小车上,细线上一端系着质量为m的小球,另一端系在支架上,当小车向左做直线运动时,细线与竖直方向的夹角为θ,此时放在小车上质量M的A物体跟小车相对静止,如图所示,则A受到的摩擦力大小和方向是(
)
A.Mgsinθ,向左 B.Mgtanθ,向右
C.Mgcosθ,向右 D.Mgtanθ,向左
1.一个木块沿倾角为α的斜面刚好能匀速下滑,若这个斜面倾角增大到β
(α<β<90°),则木块下滑加速度大小为( )
A.gsinβ B.gsin(β-α)
C.g(sinβ-tanαcosβ) D.g(sinβ-tanα)
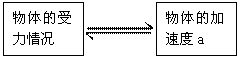
2.已知物体的运动情况求物体的受力情况
根据物体的运动情况,应用运动学公式求出物体的加速度,然后再应用牛顿第二定律求出物体所受的合外力,进而求出某些未知力。
求解以上两类动力学问题的思路,可用如下所示的框图来表示:
第一类 第二类
 |
|
||||
 |
|||||
在匀变速直线运动的公式中有五个物理量,其中有四个矢量v0、v1、a、s,一个标量t。在动力学公式中有三个物理量,其中有两个矢量F、a,一个标量m。运动学和动力学中公共的物理量是加速度a。在处理力和运动的两类基本问题时,不论由力确定运动还是由运动确定力,关键在于加速度a,a是联结运动学公式和牛顿第二定律的桥梁。
[典型例题]
例1.质量为m的物体放在倾角为α的斜面上,物体和斜面间的动摩擦系数为μ,如沿水平方向加一个力F,使物体沿斜面向上以加速度a做匀加速直线运动,如下图甲,则F多大?
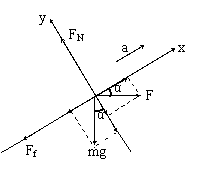
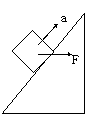 例1 [解析](1)受力分析:物体受四个力作用:重力mg、弹力FN、推力F、摩擦力Ff,(2)建立坐标:以加速度方向即沿斜面向
例1 [解析](1)受力分析:物体受四个力作用:重力mg、弹力FN、推力F、摩擦力Ff,(2)建立坐标:以加速度方向即沿斜面向
上为x轴正向,分解F和mg如图乙所示;
(3)建立方程并求解
|
y方向:FN-mgcosα-Fsinα=0 ②
f=μFN ③
三式联立求解得:
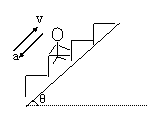 F=
F=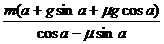
[答案]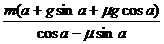
例2.如图所示,质量为m的人站在自动扶梯上,扶梯正以加速度a向上减速运动,a与水平方向的夹角为θ,求人受的支持力和摩擦力。
例2 [解析]以人为研究对象,他站在减速上升的电梯上,受到竖直向下的重力mg和竖直向上的支持力FN,还受到水平方向的静摩擦力Ff,由于物体斜向下的加速度有一个水平向左的分量,故可判断静摩擦力的方向水平向左。人受力如图的示,建立如图所示的坐标系,并将加速度分解为水平加速度ax和竖直加速度ay,如图所示,则:
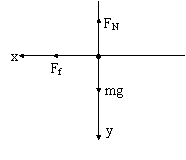 ax=acosθ
ax=acosθ
ay=asinθ
由牛顿第二定律得:
Ff=max
mg-FN=may
求得Ff=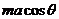 FN=
FN=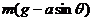
例3.风洞实验室中可产生水平方向的、大小可调节的风力,现将一套有小球的细直杆放入风洞实验室,小球孔径略大于细杆直径。(如图)
(1)当杆在水平方向上固定时,调节风力的大小,使小球在杆上匀速运动。这时小球所受的风力为小球所受重力的0.5倍,求小球与杆间的动摩擦因数。
(2)保持小球所受风力不变,使杆与水平方向间夹角为37°并固定,则小球从静止出发在细杆上滑下距离s所需时间为多少?(sin37°=0.6,cos37°=0.8)
例3 [解析](1)设小球受的风力为F,小球质量为m,因小球做匀速运动,则
F=μmg,F=0.5mg,所以μ=0.5
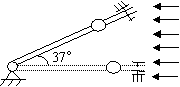 (2)如图所示,设杆对小球的支持力为FN,摩擦力为Ff,小球受力产生加速度,沿杆方向有Fcosθ+mgsinθ-Ff=ma
(2)如图所示,设杆对小球的支持力为FN,摩擦力为Ff,小球受力产生加速度,沿杆方向有Fcosθ+mgsinθ-Ff=ma
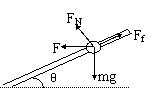 垂直杆方向有FN+Fsinθ-mgcosθ=0
垂直杆方向有FN+Fsinθ-mgcosθ=0
又Ff=μFN。
可解得a=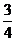 g
g
由s=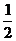 at2得 t=
at2得 t=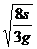
[答案](1)0.5 (2)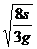
例4.如图所示,物体从斜坡上的A点由静止开始滑到斜坡底部B处,又沿水平地面滑行到C处停下,已知斜坡倾角为θ,A点高为h,物体与斜坡和地面间的动摩擦因数都是μ,物体由斜坡底部转到水平地面运动时速度大小不变,求B、C间的距离。
 例4 [解析]物体在斜坡上下滑时受力情况如图所示,根据牛顿运动定律,物体沿斜面方向和垂直斜面方向分别有
例4 [解析]物体在斜坡上下滑时受力情况如图所示,根据牛顿运动定律,物体沿斜面方向和垂直斜面方向分别有
mgsinθ-Ff=ma1
FN-mgcosθ=0
Ff=μFN
解得:a1=g(sinθ-μcosθ)
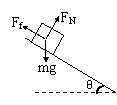 由图中几何关系可知斜坡长度为Lsinθ=h,则L=
由图中几何关系可知斜坡长度为Lsinθ=h,则L=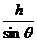
物体滑至斜坡底端B点时速度为v,根据运动学公式v2=2as,则
v=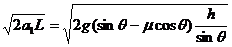
解得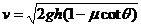
物体在水平面上滑动时,在滑动摩擦力作用下,做匀减速直线运动,根据牛顿运动定律有
μmg=ma2
则a2=μg
物体滑至C点停止,即vC=0,应用运动学公式vt2=v02+2as得
v2=2a2sBC
则sBC=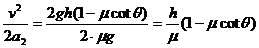
[针对训练]
1.已知物体的受力情况求物体的运动情况
根据物体的受力情况求出物体受到的合外力,然后应用牛顿第二定律F=ma求出物体的加速度,再根据初始条件由运动学公式就可以求出物体的运动情况––物体的速度、位移或运动时间。
4.牛顿第二定律的适用范围
(1)牛顿第二定律只适用于惯性参考系(相对地面静止或匀速直线运动的参考系。)
(2)牛顿第二定律只适用于宏观物体(相对于分子、原子)、低速运动(远小于光速)的情况。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com