
3.解:设物体的质量为m,在竖直方向上有:mg=F,F为摩擦力
在临界情况下,F=μFN,FN为物体所受水平弹力。又由牛顿第二定律得:
FN=ma
由以上各式得:加速度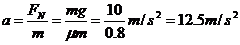
3. 如图所示,在前进的车厢的竖直后壁上放一个物体,物体与壁间的静摩擦因数μ=0.8,要使物体不致下滑,车厢至少应以多大的加速度前进?(g=10m/s2)
如图所示,在前进的车厢的竖直后壁上放一个物体,物体与壁间的静摩擦因数μ=0.8,要使物体不致下滑,车厢至少应以多大的加速度前进?(g=10m/s2)
2.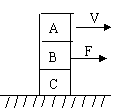 如图A、B、C为三个完全相同的物体,当水平力F作用于B上,三物体可一起匀速运动。撤去力F后,三物体仍可一起向前运动,设此时A、B间作用力为f1,B、C间作用力为f2,则f1和f2的大小为( )
如图A、B、C为三个完全相同的物体,当水平力F作用于B上,三物体可一起匀速运动。撤去力F后,三物体仍可一起向前运动,设此时A、B间作用力为f1,B、C间作用力为f2,则f1和f2的大小为( )
A.f1=f2=0 B.f1=0,f2=F
C.f1=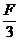 ,f2=
,f2=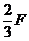 D.f1=F,f2=0
D.f1=F,f2=0
1.如图光滑水平面上物块A和B以轻弹簧相连接。在水平拉力F作用下以加速度a作直线运动,设A和B的质量分别为mA和mB,当突然撤去外力F时,A和B的加速度分别为( )
 A.0、0 B.a、0
A.0、0 B.a、0
C.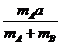 、
、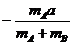 D.a、
D.a、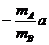
2.如图所示,倾角为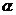 的斜面上放两物体m1和m2,用与斜面平行的力F推m1,使两物加速上滑,不管斜面是否光滑,两物体之间的作用力总为 。
的斜面上放两物体m1和m2,用与斜面平行的力F推m1,使两物加速上滑,不管斜面是否光滑,两物体之间的作用力总为 。
例1.分析:物体A和B加速度相同,求它们之间的相互作用力,采取先整体后隔离的方法,先求出它们共同的加速度,然后再选取A或B为研究对象,求出它们之间的相互作用力。
解:对A、B整体分析,则F=(m1+m2)a 所以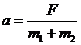
求A、B间弹力FN时以B为研究对象,则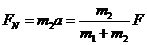 答案:B
答案:B
说明:求A、B间弹力FN时,也可以以A为研究对象则:
F-FN=m1a F-FN=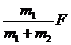 故FN=
故FN=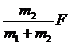
对A、B整体分析
F-μ(m1+m2)g=(m1+m2)a
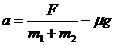
再以B为研究对象有FN-μm2g=m2a
FN-μm2g=m2
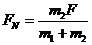
提示:先取整体研究,利用牛顿第二定律,求出共同的加速度
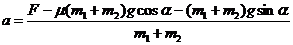 =
=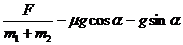
再取m2研究,由牛顿第二定律得 FN-m2gsinα-μm2gcosα=m2a 整理得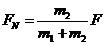
 例2.如图所示,质量为M的木板可沿倾角为θ的光滑斜面下滑,木板上站着一个质量为m的人,问(1)为了保持木板与斜面相对静止,计算人运动的加速度?(2)为了保持人与斜面相对静止,木板运动的加速度是多少?
例2.如图所示,质量为M的木板可沿倾角为θ的光滑斜面下滑,木板上站着一个质量为m的人,问(1)为了保持木板与斜面相对静止,计算人运动的加速度?(2)为了保持人与斜面相对静止,木板运动的加速度是多少?
例2.解(1)为了使木板与斜面保持相对静止,必须满足木板在斜面上的合力为零,所以人施于木板的摩擦力F应沿斜面向上,故人应加速下跑。现分别对人和木板应用牛顿第二定律得:
对木板:Mgsinθ=F。
对人:mgsinθ+F=ma人(a人为人对斜面的加速度)。
解得:a人=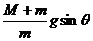 ,方向沿斜面向下。
,方向沿斜面向下。
(2)为了使人与斜面保持静止,必须满足人在木板上所受合力为零,所以木板施于人的摩擦力应沿斜面向上,故人相对木板向上跑,木板相对斜面向下滑,但人对斜面静止不动。现分别对人和木板应用牛顿第二定律,设木板对斜面的加速度为a木,则:
对人:mgsinθ=F。
对木板:Mgsinθ+F=Ma木。
解得:a木=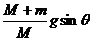 ,方向沿斜面向下。即人相对木板向上加速跑动,而木板沿斜面向下滑动,所以人相对斜面静止不动。
,方向沿斜面向下。即人相对木板向上加速跑动,而木板沿斜面向下滑动,所以人相对斜面静止不动。
答案:(1)(M+m)gsinθ/m,(2)(M+m)gsinθ/M。
[针对训练]
3.整体法与隔离法是相对统一,相辅相成的。本来单用隔离法就可以解决的连接体问题,但如果这两种方法交叉使用,则处理问题就更加方便。如当系统中各物体有相同的加速度,求系统中某两物体间的相互作用力时,往往是先用 法求出 ,再用 法求 。
[典型例题]
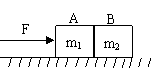 例1.两个物体A和B,质量分别为m1和m2,互相接触放在光滑水平面上,如图所示,对物体A施以水平的推力F,则物体A对物体B的作用力等于( )
例1.两个物体A和B,质量分别为m1和m2,互相接触放在光滑水平面上,如图所示,对物体A施以水平的推力F,则物体A对物体B的作用力等于( )
 A.
A.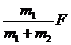 B.
B.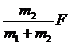
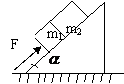 C.F D.
C.F D.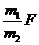
扩展:1.若m1与m2与水平面间有摩擦力且摩擦因数均为μ则对B作用力等于 。
2.隔离法:如果要求连接体间的相互作用力,必须隔离其中一个物体,对该物体应用 求解,此法称为隔离法。
1.整体法:连接体中的各物体如果 ,求加速度时可以把连接体作为一个整体。运用 列方程求解。
如果以物体系为研究对象,受到系统之外的作用力,这些力是系统受到的 力,而系统内各物体间的相互作用力为 。
应用牛顿第二定律列方程不考虑 力。如果把物体隔离出来作为研究对象,则这些内力将转换为隔离体的 力。
两个或两个以上物体相连接组成的物体系统,称为 。如果把其中某个物体隔离出来,该物体即为 。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com