
25.如图,在平面直角坐标系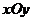 中,点
中,点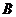 的坐标为
的坐标为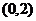 ,点
,点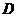 在
在 轴的正半轴上,
轴的正半轴上,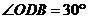 ,
,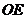 为△
为△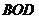 的中线,过
的中线,过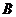 、
、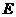 两点的抛物线
两点的抛物线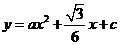 与
与 轴相交于
轴相交于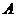 、
、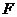 两点(
两点(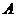 在
在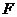 的左侧).
的左侧).
(1)求抛物线的解析式;
(2)等边△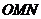 的顶点
的顶点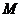 、
、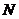 在线段
在线段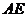 上,求
上,求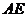 及
及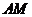 的长;
的长;
(3)点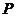 为△
为△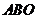 内的一个动点,设
内的一个动点,设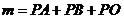 ,请直接写出
,请直接写出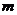 的最小值,以及
的最小值,以及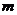 取得最小值时,线段
取得最小值时,线段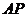 的长.
的长.
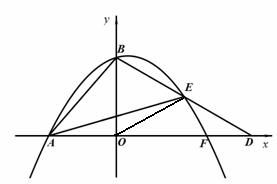
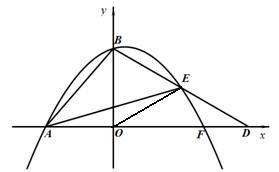
(备用图)
海淀区九年级第二学期期末测评
数学试卷答案及评分参考
24.如图,已知平面直角坐标系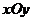 中的点
中的点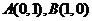 ,
,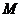 、
、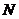 为线段
为线段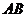 上两动点,过点
上两动点,过点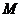 作
作 轴的平行线交
轴的平行线交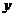 轴于点
轴于点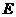 ,过点
,过点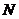 作
作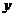 轴的平行线交
轴的平行线交 轴于点
轴于点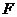 ,交直线
,交直线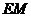 于点
于点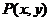 ,且
,且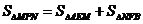 .
.
(1)
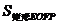 (填“>”、“=”、“<”),
(填“>”、“=”、“<”),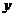 与
与 的函数关系是 (不要求写自变量的取值范围);
的函数关系是 (不要求写自变量的取值范围);
(2)当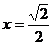 时,求
时,求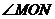 的度数;
的度数;
(3)证明: 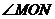 的度数为定值.
的度数为定值.
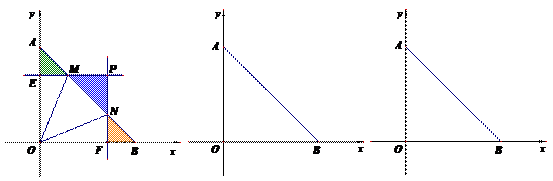
( 备用图) (备用图)
23.已知:抛物线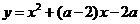 (
(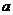 为常数,且
为常数,且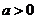 ).
).
(1)求证:抛物线与 轴有两个交点;
轴有两个交点;
(2)设抛物线与 轴的两个交点分别为
轴的两个交点分别为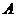 、
、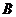 (
(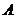 在
在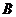 左侧),与
左侧),与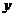 轴的交点为
轴的交点为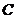 .
.
①当 时,求抛物线的解析式;
时,求抛物线的解析式;
②将①中的抛物线沿 轴正方向平移
轴正方向平移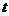 个单位(
个单位(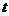 >0),同时将直线
>0),同时将直线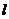 :
: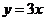 沿
沿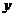 轴正方向平移
轴正方向平移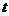 个单位.平移后的直线为
个单位.平移后的直线为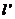 ,移动后
,移动后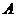 、
、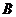 的对应点分别为
的对应点分别为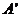 、
、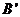 .当
.当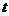 为何值时,在直线
为何值时,在直线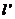 上存在点
上存在点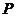 ,使得△
,使得△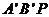 为以
为以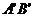 为直角边的等腰直角三角形?
为直角边的等腰直角三角形?
21.2010年1月10日,全国财政工作会议在北京召开.以下是根据2005年-2009年全国财政收入绘制的统计图的一部分(单位:百亿元).
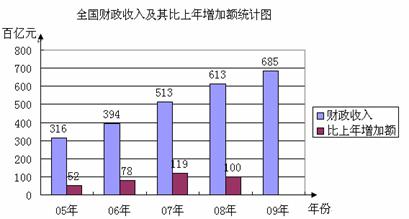
请根据提供的信息解答下列问题:
(1) 完成统计图;
(2) 计算2005年-2009年这五年全国财政收入比上年增加额的平均数;
(3) 如果2010年全国财政收入按照(2)中求出的平均数增长,预计2010年全国财政收入的金额达到多少百亿元?
20. 已知:如图,点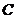 在以
在以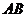 为直径的⊙
为直径的⊙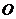 上,点
上,点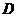 在
在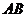 的延长线上,
的延长线上,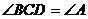 .
.
(1)求证: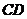 为⊙
为⊙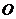 的切线;
的切线;
 (2) 过点
(2) 过点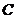 作
作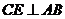 于
于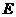 .若
.若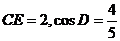 ,求⊙
,求⊙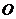 的半径.
的半径.
19. 已知:如图,梯形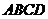 中,
中,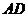 ∥
∥ ,
,
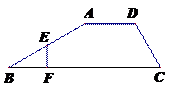
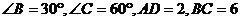 ,
,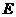 为
为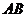 中点,
中点,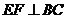 于
于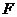 ,求
,求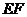 的长.
的长.
18. 列方程(组)解应用题:
小明乘坐火车从某地到上海去参观世博园,已知此次行程为2160千米,城际直达动车组的平均时速是特快列车的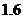 倍.小明购买火车票时发现,乘坐动车组比乘坐特快列车少用6小时.求小明乘坐动车组到上海需要的时间.
倍.小明购买火车票时发现,乘坐动车组比乘坐特快列车少用6小时.求小明乘坐动车组到上海需要的时间.
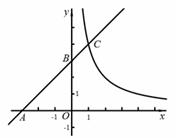
17.如图,直线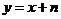 与
与 轴交于点
轴交于点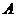 ,与
,与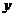 轴交于点
轴交于点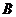 ,与双曲线
,与双曲线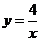 在第一象限内交于点
在第一象限内交于点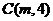 .
.
(1)求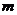 和
和 的值;
的值;
 (2)若将直线
(2)若将直线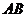 绕点
绕点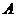 顺时针旋转
顺时针旋转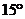 得到直线
得到直线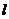 ,求直线
,求直线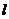 的解析式.
的解析式.
16.已知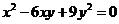 ,求代数式
,求代数式 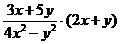 的值.
的值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com