
3、已知集合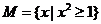 ,
,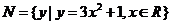 ,则
,则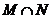 =( )
=( )
A.Æ B.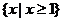 C.
C.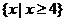 D.{
D.{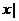
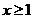 或
或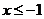 }
}
2、设集合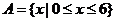 ,
,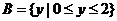 ,下列对应不是从集合A到集合B的映射的是( )
,下列对应不是从集合A到集合B的映射的是( )
A.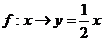 B.
B.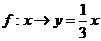
C.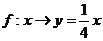 D.
D.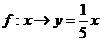
1、已知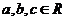 ,且
,且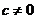 ,则下列命题正确的是( )
,则下列命题正确的是( )
A.如果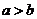 ,那么
,那么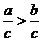 B.如果
B.如果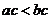 ,那么
,那么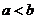
C.如果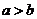 ,那么
,那么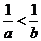 D.如果
D.如果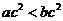 ,那么
,那么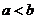
(一)解答题:
1、已知正方体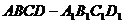 中,
中,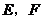 分别为
分别为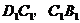 的中点,
的中点,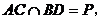
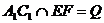 求证:(1)
求证:(1)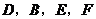 四点共面;(2)若
四点共面;(2)若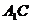 交平面
交平面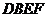 于
于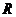 点,则
点,则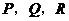 三点共线。
三点共线。
2、已知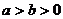 ,求证:
,求证: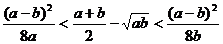 。
。
3、设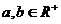 ,且
,且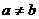 ,求证:
,求证: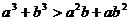 。
。
4、已知: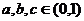 。求证:
。求证: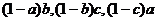 中至少有一个不大于
中至少有一个不大于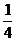 。
。
5、已知 。求证:(1)
。求证:(1)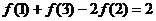 ;
;
(2)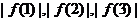 中至少有一个不小于
中至少有一个不小于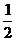 。
。
例1、(06陕西)某校从8名教师中选派4名教师同时去4个边远地区支教(每地1人),其中甲和乙不同去,甲和丙只能同去或同不去,则不同的选派方案共有 种。(600种)
(二)解答题:
2、(07湖北21)(I)用数学归纳法证明:当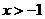 时,
时,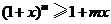 ;
;
(II)对于 ,已知
,已知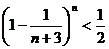 ,
,
求证: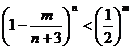 ,
,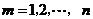 ;
;
(III)求出满足等式 的所有正整数
的所有正整数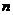 。
。
解法1:(Ⅰ)证:用数学归纳法证明:
(ⅰ)当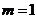 时,原不等式成立;当
时,原不等式成立;当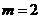 时,左边
时,左边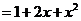 ,右边
,右边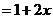 ,
,
因为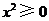 ,所以左边
,所以左边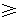 右边,原不等式成立;
右边,原不等式成立;
(ⅱ)假设当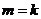 时,不等式成立,即
时,不等式成立,即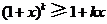 ,则当
,则当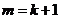 时,
时,
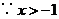 ,
,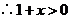 ,于是在不等式
,于是在不等式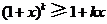 两边同乘以
两边同乘以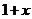 得
得
 ,
,
所以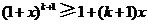 .即当
.即当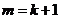 时,不等式也成立.
时,不等式也成立.
综合(ⅰ)(ⅱ)知,对一切正整数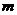 ,不等式都成立.
,不等式都成立.
(Ⅱ)证:当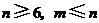 时,由(Ⅰ)得
时,由(Ⅰ)得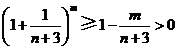 ,
,
于是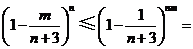
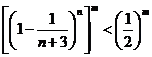 ,
,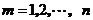 .
.
(Ⅲ)解:由(Ⅱ)知,当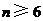 时,
时,
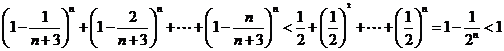 ,
,
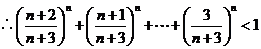 .
.
即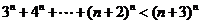 .即当
.即当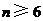 时,不存在满足该等式的正整数
时,不存在满足该等式的正整数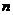 .
.
故只需要讨论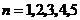 的情形:
的情形:
当 时,
时,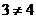 ,等式不成立;
,等式不成立;
当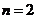 时,
时,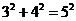 ,等式成立;
,等式成立;
当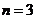 时,
时,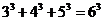 ,等式成立;
,等式成立;
当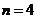 时,
时,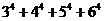 为偶数,而
为偶数,而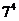 为奇数,故
为奇数,故 ,等式不成立;
,等式不成立;
当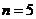 时,同
时,同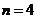 的情形可分析出,等式不成立.
的情形可分析出,等式不成立.
综上,所求的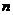 只有
只有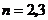 .
.
解法2:(Ⅰ)证:当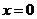 或
或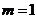 时,原不等式中等号显然成立,下用数学归纳法证明:
时,原不等式中等号显然成立,下用数学归纳法证明:
当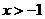 ,且
,且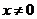 时,
时,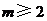 ,
,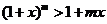 . ①
. ①
(ⅰ)当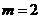 时,左边
时,左边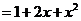 ,右边
,右边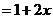 ,因为
,因为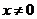 ,所以
,所以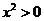 ,即左边
,即左边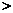 右边,不等式①成立;
右边,不等式①成立;
(ⅱ)假设当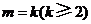 时,不等式①成立,即
时,不等式①成立,即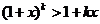 ,则当
,则当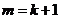 时,
时,
因为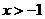 ,所以
,所以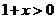 .又因为
.又因为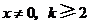 ,所以
,所以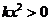 .
.
于是在不等式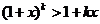 两边同乘以
两边同乘以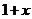 得
得
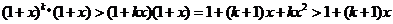 ,
,
所以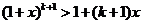 .即当
.即当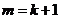 时,不等式①也成立.
时,不等式①也成立.
综上所述,所证不等式成立.
(Ⅱ)证:当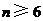 ,
,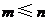 时,
时, ,
,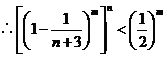 ,
,
而由(Ⅰ),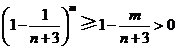 ,
,
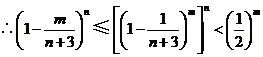 .
.
(Ⅲ)解:假设存在正整数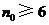 使等式
使等式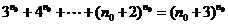 成立,
成立,
即有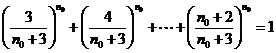 . ②
. ②
又由(Ⅱ)可得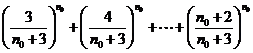
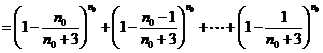
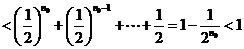 ,与②式矛盾.
,与②式矛盾.
故当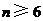 时,不存在满足该等式的正整数
时,不存在满足该等式的正整数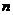 .
.
下同解法1.
3、(06陕西22)已知函数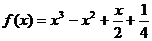 ,且存在
,且存在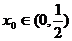 ,使
,使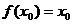 。
。
(I)证明: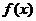 是
是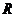 上的单调增函数;(II)设
上的单调增函数;(II)设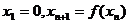 ,
,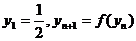
其中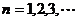 。证明:
。证明: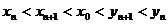 ;(III)证明:
;(III)证明: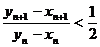 。
。
解: (I)∵f '(x)=3x2-2x+ = 3(x-)2+ >0 , ∴f(x)是R上的单调增函数.
(II)∵0<x0< , 即x1<x0<y1.又f(x)是增函数, ∴f(x1)<f(x0)<f(y1).即x2<x0<y2.
又x2=f(x1)=f(0)=>0 =x1, y2=f(y1)=f()=<=y1,综上, x1<x2<x0<y2<y1.
用数学归纳法证明如下:
(1)当n=1时,上面已证明成立.
(2)假设当n=k(k≥1)时有xk<xk+1<x0<yk+1<yk .
当n=k+1时,由f(x)是单调增函数,有f(xk)<f(xk+1)<f(x0)<f(yk+1)<f(yk),∴xk+1<xk+2<x0<yk+2<yk+1
由(1)(2)知对一切n=1,2,…,都有xn<xn+1<x0<yn+1<yn.
(III) = = yn2+xnyn+xn2-(yn+xn)+ ≤(yn+xn)2-(yn+xn)+
=[(yn+xn)-]2+ . 由(Ⅱ)知 0<yn+xn<1.∴- < yn+xn- < , ∴ < ()2+ =
4、(06江西22)已知数列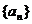 满足:
满足: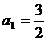 ,且
,且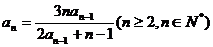
(1)求数列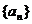 的通项公式;
的通项公式;
(2)证明:对于一切正整数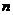 ,不等式
,不等式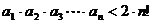 。
。
解:
(1)
将条件变为:1-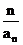 =
=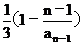 ,因此{1-
,因此{1-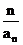 }为一个等比数列,其首项为
}为一个等比数列,其首项为
1-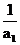 =
=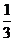 ,公比
,公比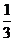 ,从而1-
,从而1-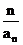 =
=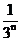 ,据此得an=
,据此得an=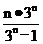 (n³1)…………1°
(n³1)…………1°
(2)
证:据1°得,a1·a2·…an=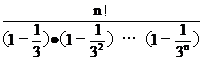
为证a1·a2·……an<2·n!
只要证nÎN*时有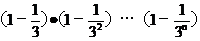 >
>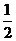 …………2°
…………2°
显然,左端每个因式都是正数,先证明,对每个nÎN*,有
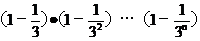 ³1-(
³1-(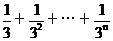 )…………3°
)…………3°
用数学归纳法证明3°式:
(i) n=1时,3°式显然成立,
(ii) 设n=k时,3°式成立,
即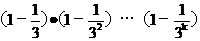 ³1-(
³1-(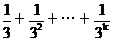 )
)
则当n=k+1时,
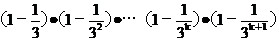 ³(1-(
³(1-(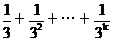 ))·(
))·(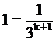 )
)
=1-(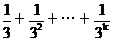 )-
)-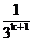 +
+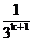 (
(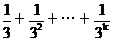 )
)
³1-(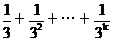 +
+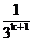 )即当n=k+1时,3°式也成立。
)即当n=k+1时,3°式也成立。
故对一切nÎN*,3°式都成立。
利用3°得,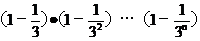 ³1-(
³1-(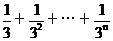 )=1-
)=1-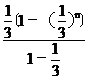
=1-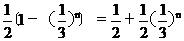 >
>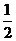
故2°式成立,从而结论成立。
(一)选择题:
1、(07上海)设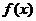 是定义在正整数集上的函数,且
是定义在正整数集上的函数,且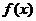 满足:“当
满足:“当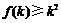 成立时,总可推 出
成立时,总可推 出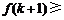
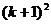 成立”.那么,下列命题总成立的是( )
成立”.那么,下列命题总成立的是( )
A、若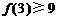 成立,则当
成立,则当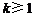 时,均有
时,均有 成立
成立
B、若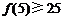 成立,则当
成立,则当 时,均有
时,均有 成立
成立
C、若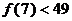 成立,则当
成立,则当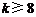 时,均有
时,均有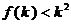 成立
成立
D、若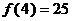 成立,则当
成立,则当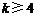 时,均有
时,均有 成立
成立
例1、(06安徽21)数列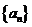 的前
的前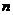 项和为
项和为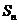 ,已知
,已知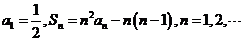
(Ⅰ)写出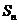 与
与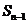 的递推关系式
的递推关系式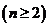 ,并求
,并求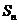 关于
关于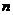 的表达式;(Ⅱ)设
的表达式;(Ⅱ)设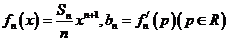 ,求数列
,求数列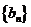 的前
的前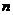 项和
项和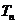 。
。
解:由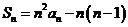
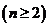 得:
得: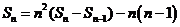 ,即
,即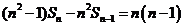 ,所以
,所以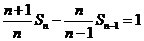 ,对
,对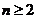 成立。
成立。
由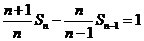 ,
,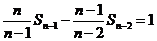 ,…,
,…,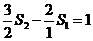 相加得:
相加得: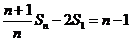 ,又
,又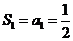 ,所以
,所以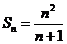 ,当
,当 时,也成立。
时,也成立。
(Ⅱ)由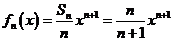 ,得
,得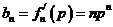 。
。
而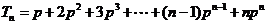 ,
,
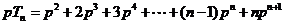 ,
,
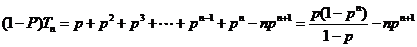 。
。
例2、(07广东21)已知函数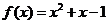 ,
,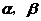 是方程
是方程 的两个根(
的两个根(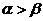 ),
),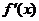 是
是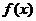 的导数,设
的导数,设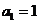 ,
,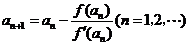 .
.
(1)求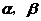 的值;
的值;
(2)证明:对任意的正整数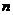 ,都有
,都有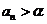 ;
;
(3)记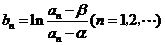 ,求数列
,求数列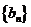 的前
的前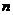 项和
项和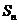 .
.
已知函数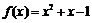 ,
,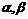 是方程f(x)=0的两个根
是方程f(x)=0的两个根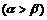 ,
,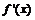 是f(x)的导数;设
是f(x)的导数;设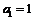 ,
,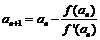 (n=1,2,……)
(n=1,2,……)
(1)求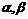 的值;
的值;
(2)证明:对任意的正整数n,都有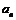 >a;
>a;
(3)记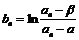 (n=1,2,……),求数列{bn}的前n项和Sn。
(n=1,2,……),求数列{bn}的前n项和Sn。
解析:(1)∵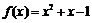 ,
,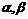 是方程f(x)=0的两个根
是方程f(x)=0的两个根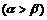 ,
,
∴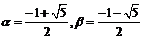 ;
;
(2)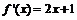 ,
,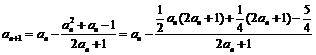
=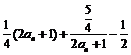 ,∵
,∵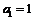 ,∴有基本不等式可知
,∴有基本不等式可知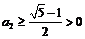 (当且仅当
(当且仅当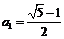 时取等号),∴
时取等号),∴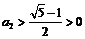 同,样
同,样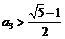 ,……,
,……,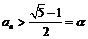 (n=1,2,……),
(n=1,2,……),
(3)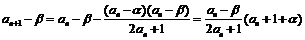 ,而
,而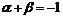 ,即
,即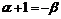 ,
,
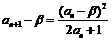 ,同理
,同理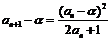 ,
,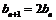 ,又
,又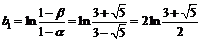
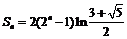 。
。
例3、(05重庆22)数列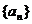 满足
满足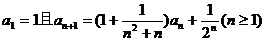 .
.
(Ⅰ)用数学归纳法证明: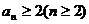 ;
;
(Ⅱ)已知不等式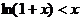 对
对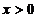 成立,证明:
成立,证明: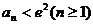 ,其中无理数e=2.71828…。
,其中无理数e=2.71828…。
(Ⅰ)证明:(1)当n=2时,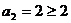 ,不等式成立.
,不等式成立.
(2)假设当 时不等式成立,即
时不等式成立,即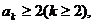
那么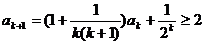 . 这就是说,当
. 这就是说,当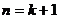 时不等式成立.
时不等式成立.
根据(1)、(2)可知: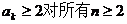 成立.
成立.
(Ⅱ)证法一:
由递推公式及(Ⅰ)的结论有
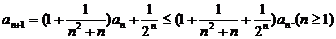
两边取对数并利用已知不等式得
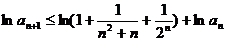
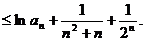 故
故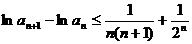
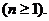
上式从1到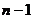 求和可得
求和可得
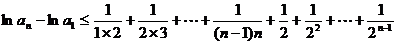
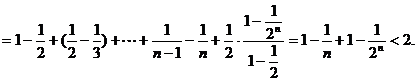
即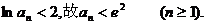
(Ⅱ)证法二:
由数学归纳法易证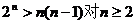 成立,故
成立,故
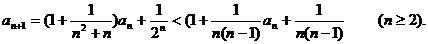
令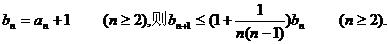
取对数并利用已知不等式得 
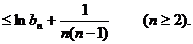
上式从2到n求和得 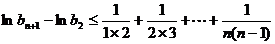
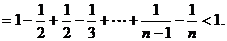
因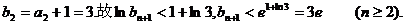
故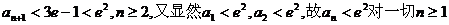 成立。
成立。
(二)填空题:7、方程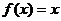 的根称为
的根称为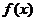 的不动点,若函数
的不动点,若函数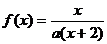 有唯一不动点,且
有唯一不动点,且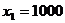 ,
,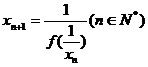 ,则
,则 。
。
(一)选择题:
1、已知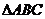 中,若
中,若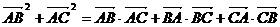 ,则
,则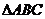 是( )
是( )
A、等边三角形 B、钝角三角形 C、锐角三角形 D、直角三角形
分析:右边全变为三角形的边,用三角形余弦定理。选D。
2、如果函数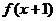 是偶函数,那么函数
是偶函数,那么函数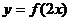 的图象的一条对称轴是直线( )
的图象的一条对称轴是直线( )
A、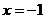 B、
B、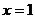 C、
C、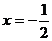 D、
D、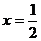
3、设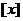 表示不超过
表示不超过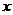 的最大整数,则关于
的最大整数,则关于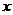 的不等式
的不等式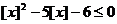 的解集是( )
的解集是( )
A、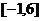 B、[0,6]
C、[
B、[0,6]
C、[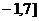 D、[0,7]
D、[0,7]
4、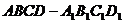 是单位正方体,黑、白两个蚂蚁从点
是单位正方体,黑、白两个蚂蚁从点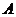 出发沿棱向前爬行,每爬完一条棱称为“爬完一段”。白蚂蚁爬行的路线是
出发沿棱向前爬行,每爬完一条棱称为“爬完一段”。白蚂蚁爬行的路线是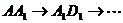 ,黑蚂蚁爬行的路线是
,黑蚂蚁爬行的路线是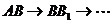 ,它们都遵循如下规则:所爬行的第
,它们都遵循如下规则:所爬行的第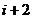 段与第
段与第 段所在直线必须是异面直线(其中
段所在直线必须是异面直线(其中 是自然数)。设黑、白蚂蚁都爬完
是自然数)。设黑、白蚂蚁都爬完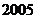 段后各自停止在正方体的某个顶点处,这时黑、白蚂蚁的距离是( )
段后各自停止在正方体的某个顶点处,这时黑、白蚂蚁的距离是( )
A、1
B、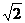 C、
C、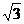 D、0
D、0
5、已知向量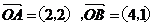 ,在
,在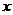 轴上一点
轴上一点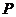 使
使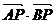 有最小值,则点
有最小值,则点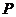 的坐标是( )
的坐标是( )
A、 B、(2,0)
C、(3,0)
D、(4,0)
B、(2,0)
C、(3,0)
D、(4,0)
6、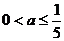 是函数
是函数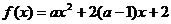 在区间(
在区间(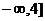 上为减函数的( )
上为减函数的( )
A、充分不必要条件 B、必要不充分条件
C、充要条件 D、既不充分也不必要条件
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com