
42、(广东省韶关市2008届高三第一次调研考试)如图,在三棱拄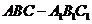 中,
中,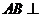 侧面
侧面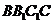 ,已知
,已知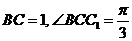

(Ⅰ)求证: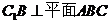 ;
;
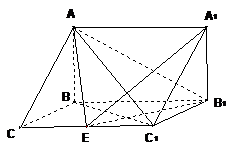 (Ⅱ)试在棱
(Ⅱ)试在棱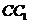 (不包含端点
(不包含端点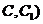 上确定一点
上确定一点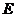 的位置,使得
的位置,使得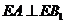 ;
;
(Ⅲ) 在(Ⅱ)的条件下,求二面角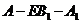 的平面角的正切值.
的平面角的正切值.
证(Ⅰ)因为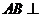 侧面
侧面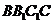 ,故
,故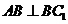
在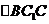 中,
中,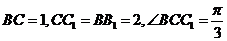
由余弦定理有
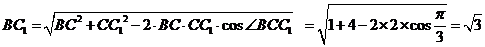
 故有
故有 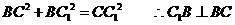
而 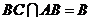 且
且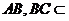 平面
平面
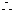
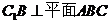
(Ⅱ)由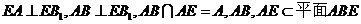
从而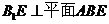 且
且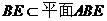 故
故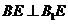
不妨设 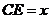 ,则
,则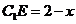 ,则
,则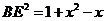
又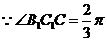 则
则
在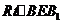 中有
中有
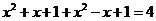 从而
从而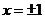 (舍负)
(舍负)
故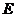 为
为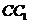 的中点时,
的中点时,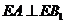
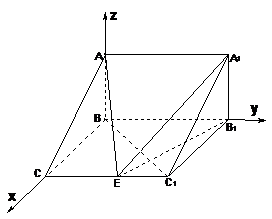 法二:以
法二:以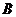 为原点
为原点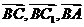 为
为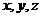 轴,设
轴,设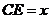 ,则
,则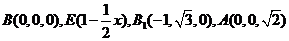 由
由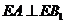 得
得 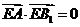 即
即

化简整理得 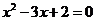
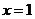 或
或 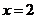
当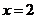 时
时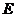 与
与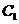 重合不满足题意
重合不满足题意
当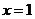 时
时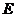 为
为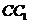 的中点
的中点
故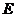 为
为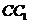 的中点使
的中点使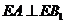
(Ⅲ)取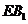 的中点
的中点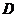 ,
, 的中点
的中点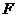 ,
,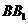 的中点
的中点 ,
,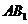 的中点
的中点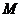
连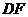 则
则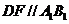 ,连
,连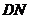 则
则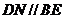 ,连
,连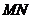 则
则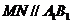
连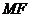 则
则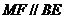 ,且
,且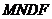 为矩形,
为矩形,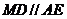
又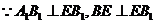 故
故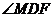 为所求二面角的平面角
为所求二面角的平面角
 在
在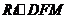 中,
中,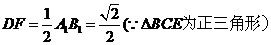
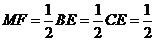

法二:由已知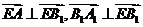 ,
所以二面角
,
所以二面角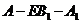 的平面角
的平面角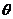 的大小为向量
的大小为向量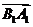 与
与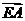 的夹角
的夹角
因为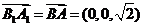
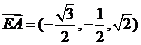
故
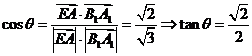
41、(广东省汕头市澄海区2008年第一学期期末考试)如图,已知正四棱柱ABCD-A1B1C1D1中,底面边长AB=2,侧棱BB1的长为4,过点B作B1C的垂线交侧棱CC1于点E,交B1C于点F,
(1)求证:A1C⊥平面BDE;
(2)求A1B与平面BDE所成角的正弦值。
(3)设F是CC1上的动点(不包括端点C),求证:△DBF是锐角三角形。
(1)证明:由正四棱柱性质知A1B1⊥平面BCC1B1,A1A⊥平面ABCD,
所以B1C、AC分别是A1C在平面CC1B1B、平面ABCD上的射影
∵ B1C⊥BE, AC⊥BD, ∴A1C⊥BE , A1C⊥BD, (2分)
∴ A1C⊥平面BDE (4分)。 (直接指出根据三垂线定理得“A1C⊥BE , A1C⊥BD”而推出结论的不扣分)
(2)解:以DA、DC、DD1所在直线分别为x、y、z轴,建立坐标系,则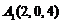 ,
,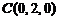 ,
,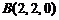 ,∴
,∴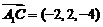 ,
,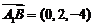 (6分)
(6分)
∴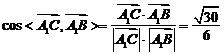 (7分)
(7分)
设A1C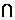 平面BDE=K,
平面BDE=K,
由(1)可知,∠A1BK为A1B与平面BDE所成角,(8分)
∴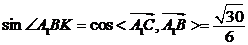 (9分)
(9分)
(3)证明:设点F的坐标为(0, 2, z)(0<z≤4), 则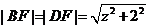 ,
,
又|DB|= ,故△DBF是等腰三角形,要证明它为锐角三角形,只需证明其顶角∠DFB为锐角则可。
(11分)
,故△DBF是等腰三角形,要证明它为锐角三角形,只需证明其顶角∠DFB为锐角则可。
(11分)
由余弦定理得cos∠DFB=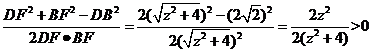
∴∠DFB为锐角, (13分)
即不论点F为CC1上C点除外的任意一点, △DFB总是锐角三角形.(14分)
说明: 若没有说明三角形为等腰三角形而只证明一个角是锐角,或只证明底角是锐角的“以偏概全”情况应扣2分)
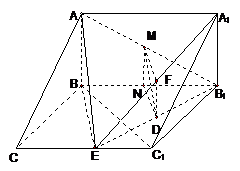
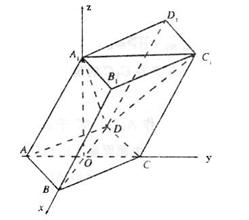
40、(广东省汕头市潮阳一中2008年高三模拟)如图,棱柱ABCD-A1B1C1D1的所有棱长都等于2,∠ABC=60°,平面AA1C1C⊥平面ABCD,∠A1AC=60°。
(Ⅰ)证明:BD⊥AA1;
(Ⅱ)求二面角D-A1A-C的平面角的余弦值;
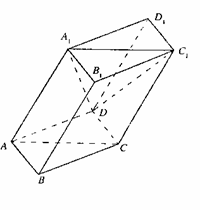 (Ⅲ)在直线CC1上是否存在点P,使BP//平面DA1C1?若存在,求出点P的位置;若不存在,说明理由。
(Ⅲ)在直线CC1上是否存在点P,使BP//平面DA1C1?若存在,求出点P的位置;若不存在,说明理由。
解:连接BD交AC于O,则BD⊥AC,
连接A1O
在△AA1O中,AA1=2,AO=1,
∠A1AO=60°
∴A1O2=AA12+AO2-2AA1·Aocos60°=3
∴AO2+A1O2=A12
∴A1O⊥AO,由于平面AA1C1C⊥
平面ABCD,
所以A1O⊥底面ABCD
∴以OB、OC、OA1所在直线为x轴、y轴、z轴建立如图所示空间直角坐标系,则A(0,-1,0),B(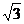 ,0,0),C(0,1,0),D(-
,0,0),C(0,1,0),D(-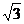 ,0,0),A1(0,0,
,0,0),A1(0,0,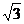 )
)
 ……………………2分
……………………2分
(Ⅰ)由于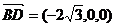
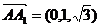
则
∴BD⊥AA1……………………4分
(Ⅱ)由于OB⊥平面AA1C1C
∴平面AA1C1C的法向量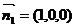
设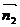 ⊥平面AA1D
⊥平面AA1D
则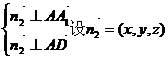
得到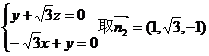 ……………………6分
……………………6分
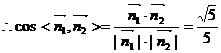
所以二面角D-A1A-C的平面角的余弦值是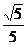 ……………………8分
……………………8分
(Ⅲ)假设在直线CC1上存在点P,使BP//平面DA1C1
设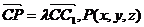
则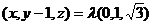
得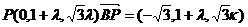 ……………………9分
……………………9分
设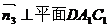
则 设
设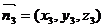
得到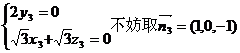 ……………………10分
……………………10分
又因为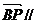 平面DA1C1
平面DA1C1
则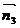 ·
·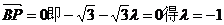
即点P在C1C的延长线上且使C1C=CP……………………12分
法二:在A1作A1O⊥AC于点O,由于平面AA1C1C⊥平面
ABCD,由面面垂直的性质定理知,A1O⊥平面ABCD,
又底面为菱形,所以AC⊥BD
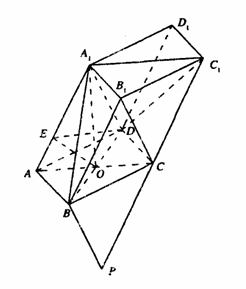
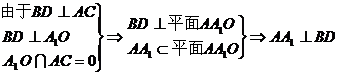
……………………4分
(Ⅱ)在△AA1O中,A1A=2,∠A1AO=60°
∴AO=AA1·cos60°=1
所以O是AC的中点,由于底面ABCD为菱形,所以
O也是BD中点
由(Ⅰ)可知DO⊥平面AA1C
过O作OE⊥AA1于E点,连接OE,则AA1⊥DE
则∠DEO为二面角D-AA1-C的平面角
……………………6分
在菱形ABCD中,AB=2,∠ABC=60°
∴AC=AB=BC=2
∴AO=1,DO=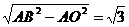
在Rt△AEO中,OE=OA·sin∠EAO=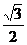
DE=
∴cos∠DEO=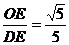
∴二面角D-A1A-C的平面角的余弦值是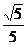 ……………………8分
……………………8分
(Ⅲ)存在这样的点P
连接B1C,因为A1B1 AB
AB DC
DC
∴四边形A1B1CD为平行四边形。
∴A1D//B1C
在C1C的延长线上取点P,使C1C=CP,连接BP……………………10分
因B1B CC1,……………………12分
CC1,……………………12分
∴BB1 CP
CP
∴四边形BB1CP为平行四边形
则BP//B1C
 ∴BP//A1D
∴BP//A1D
∴BP//平面DA1C1
39、(广东省揭阳市2008年高中毕业班高考调研测试) 在三棱锥
在三棱锥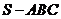 中,
中,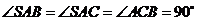 ,
,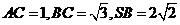 .
.
(1)
求三棱锥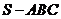 的体积;
的体积;
(2)
证明: ;
;
(3) 求异面直线SB和AC所成角的余弦值。
(1)解:∵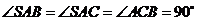
∴ 且
且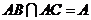 ,
,
∴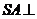 平面
平面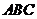 ------------ ----------------2分
------------ ----------------2分
 在
在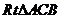 中,
中,
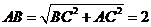 ,
,
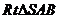 中,
中,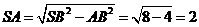
∵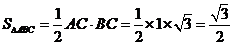 ,
,
∴ .--------------4分
.--------------4分
(2)证法1:由(1)知SA=2, 在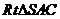 中,
中,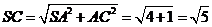 ---6分
---6分
∵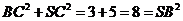 ,∴
,∴ -------------------8分
-------------------8分
证法2:由(1)知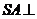 平面
平面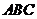 ,∵
,∵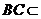 面
面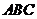 ,
,
∴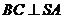 ,∵
,∵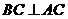 ,
, ,∴
,∴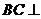 面
面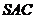
又∵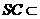 面
面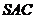 ,∴
,∴
(3) 解法1:分别取AB、SA、 BC的中点D、E、F,
连结ED、DF、EF、AF,则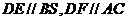 ,
,
∴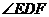 (或其邻补角)就是异面直线SB和AC所成的角----------10分
(或其邻补角)就是异面直线SB和AC所成的角----------10分
 ∵
∵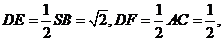
在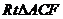 中,
中,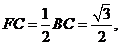
∴ ,
,
在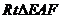 中,
中,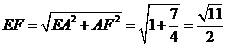
在△DEF中,由余弦定理得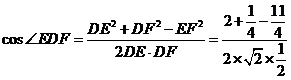
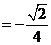
∴异面直线SB和AC所成的角的余弦值为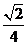 -------------------------14分
-------------------------14分
解法2:以点A为坐标原点,AC所在的直线为y轴建立空间直角坐标系如图
则可得点A(0,0,0),C(0,1,0),B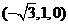
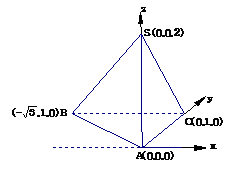 ∴
∴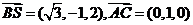
设异面直线SB和AC所成的角为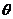
则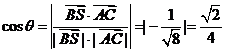
∴异面直线SB和AC所成的角的余弦值为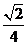 。
。
38、(广东省惠州市2008届高三第三次调研考试)如图,P-ABCD是正四棱锥,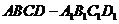 是正方体,
是正方体,
其中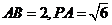

(1)求证: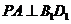 ;
;
(2)求平面PAD与平面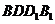 所成的锐二面角
所成的锐二面角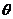 的余弦值;
的余弦值;
(3)求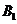 到平面PAD的距离
到平面PAD的距离
解法一:以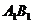 为
为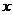 轴,
轴,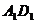 为
为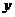 轴,
轴,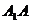 为
为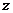 轴建立空间直角坐标系…………1分
轴建立空间直角坐标系…………1分
(1)设E是BD的中点, P-ABCD是正四棱锥,∴
P-ABCD是正四棱锥,∴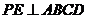 …………2分
…………2分
又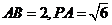 ,
∴
,
∴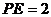 ∴
∴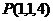 ……………………………3分
……………………………3分
∴
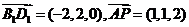 ………………………………………………4分
………………………………………………4分
∴ 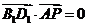 即
即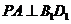 ………………………………………5分
………………………………………5分
(2)设平面PAD的法向量是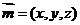 ,…………………………………………6分
,…………………………………………6分
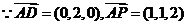 ……………………………………………………7分
……………………………………………………7分
∴
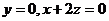 取
取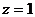 得
得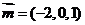 ,………………………………8分
,………………………………8分
又平面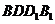 的法向量是
的法向量是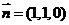 …………………………………………9分
…………………………………………9分
∴ 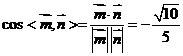 ∴
∴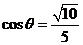 …………………10分
…………………10分
(3)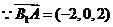 …………………………………………………………………11分
…………………………………………………………………11分
∴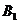 到平面PAD的距离
到平面PAD的距离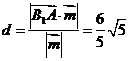 ……………………………………14分
……………………………………14分
解法二:
(1)设AC与BD交点为O,连PO;∵P-ABCD是正四棱锥,∴PO⊥面ABCD,……1分
∴AO为PA在平面ABCD上的射影, 又ABCD为正方形,∴AO⊥BD,…………3分
由三垂线定理知PA⊥BD,而BD∥B1D1;∴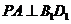 …………………………5分
…………………………5分
(2)由题意知平面PAD与平面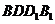 所成的锐二面角为二面角A-PD-B;……6分
所成的锐二面角为二面角A-PD-B;……6分
∵AO⊥面PBD,过O作OE垂直PD于E,连AE,
则由三垂线定理知∠AEO为二面角A-PD-B的平面角; ……………………8分
可以计算得,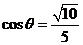 …………………………………………………………10分
…………………………………………………………10分
(3)设B1C1与BC的中点分别为M、N;则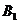 到平面PAD的距离为M到平面PAD的距离;
到平面PAD的距离为M到平面PAD的距离;
由VM-PAD=VP-ADM求得 。
。
37、 (广东省佛山市2008年高三教学质量检测一)如图,在组合体中,
(广东省佛山市2008年高三教学质量检测一)如图,在组合体中,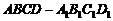 是一个长方体,
是一个长方体,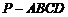 是一个四棱锥.
是一个四棱锥.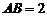 ,
,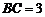 ,点
,点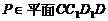 且
且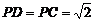 .
.
(Ⅰ)证明: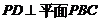 ;
;
(Ⅱ)求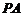 与平面
与平面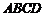 所成的角的正切值;
所成的角的正切值;
(Ⅲ)若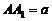 ,当
,当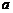 为何值时,
为何值时,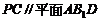 .
.
(Ⅰ)证明:因为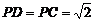 ,
,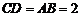 ,所以
,所以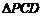 为等腰直角三角形,所以
为等腰直角三角形,所以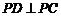 .
……1分
.
……1分
因为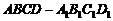 是一个长方体,所以
是一个长方体,所以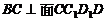 ,而
,而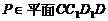 ,所以
,所以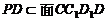 ,所以
,所以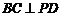 .
……3分
.
……3分
因为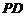 垂直于平面
垂直于平面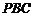 内的两条相交直线
内的两条相交直线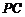 和
和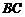 ,由线面垂直的判定定理,可得
,由线面垂直的判定定理,可得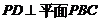 .…4分
.…4分
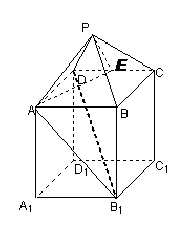 (Ⅱ)解:过
(Ⅱ)解:过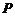 点在平面
点在平面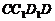 作
作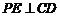 于
于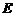 ,连接
,连接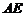 .……5分
.……5分
因为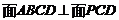 ,所以
,所以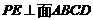 ,所以
,所以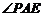 就是
就是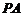 与平面
与平面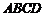 所成的角.……6分
所成的角.……6分
因为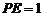 ,
,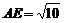 ,所以
,所以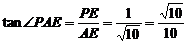 . ……7分
. ……7分
所以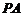 与平面
与平面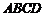 所成的角的正切值为
所成的角的正切值为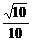 .
……8分
.
……8分
(Ⅲ)解:当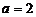 时,
时,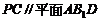 .
……9分
.
……9分
当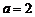 时,四边形
时,四边形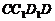 是一个正方形,所以
是一个正方形,所以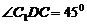 ,而
,而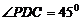 ,所以
,所以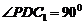 ,所以
,所以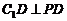 .
……10分
.
……10分
而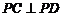 ,
,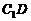 与
与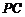 在同一个平面内,所以
在同一个平面内,所以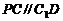 . ……11分
. ……11分
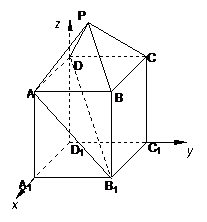 而
而 ,所以
,所以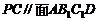 ,所以
,所以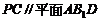 . ……12分
. ……12分
方法二:(Ⅰ)如图建立空间直角坐标系,设棱长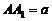 ,则有
,则有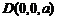 ,
,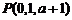 ,
,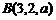 ,
, .
……2分
.
……2分
于是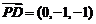 ,
,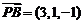 ,
, ,所以
,所以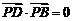 ,
,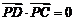 .……3分
.……3分
所以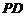 垂直于平面
垂直于平面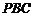 内的两条相交直线
内的两条相交直线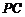 和
和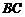 ,由线面垂直的判定定理,可得
,由线面垂直的判定定理,可得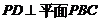 .
……4分
.
……4分
(Ⅱ)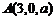 ,所以
,所以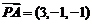 ,而平面
,而平面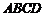 的一个法向量为
的一个法向量为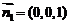 .…5分
.…5分
所以 .
……6分
.
……6分
所以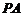 与平面
与平面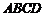 所成的角的正弦值为
所成的角的正弦值为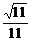 .
……7分
.
……7分
所以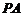 与平面
与平面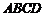 所成的角的正切值为
所成的角的正切值为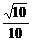 .
……8分
.
……8分
(Ⅲ)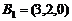 ,所以
,所以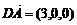 ,
,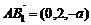 .设平面
.设平面 的法向量为
的法向量为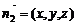 ,则有
,则有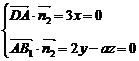 ,令
,令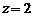 ,可得平面
,可得平面 的一个法向量为
的一个法向量为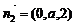 .
……10分
.
……10分
若要使得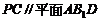 ,则要
,则要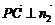 ,即
,即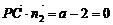 ,解得
,解得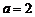 .…11分
.…11分
所以当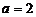 时,
时,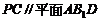 .
.
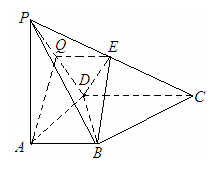
36、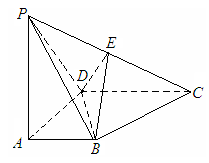 (广东省2008届六校第二次联考)如图所示, 四棱锥P
(广东省2008届六校第二次联考)如图所示, 四棱锥P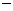 ABCD底面是直角梯形,
ABCD底面是直角梯形,  底面ABCD, E为PC的中点, PA=AD=AB=1.
底面ABCD, E为PC的中点, PA=AD=AB=1.
(1)证明: 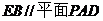 ;
;
(2)证明: 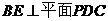 ;
;
(3)求三棱锥B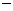 PDC的体积V.
PDC的体积V.
证明:(1)取PD中点Q, 连EQ , AQ , 则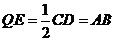 …1分
…1分
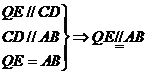 …………………………………………2分
…………………………………………2分
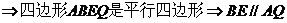 ………………3分
………………3分
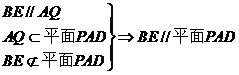 ………………………5分
………………………5分
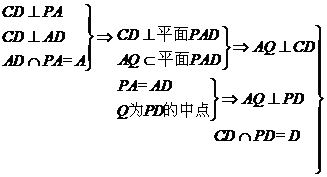 (2)
(2) 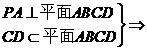
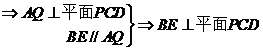 . ………………………………………10分
. ………………………………………10分
解:(3)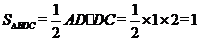 …………………………………11分
…………………………………11分
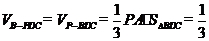 .
.
35、(甘肃省兰州一中2008届高三上期期末考试)在棱长AB=AD=2,AA1=3的长方体AC1中,点E是平面BCC1B1上动点,点F是CD的中点.
(Ⅰ)试确定E的位置,使D1E⊥平面AB1F;
(Ⅱ)求二面角B1-AF-B的大小.
解:(Ⅰ)以A为原点,AB、AD、AA1所在直线分别为x轴、y轴、z轴建立空间直角坐标系,
 A(0,0,0),F(1,2,0),B1(2,0,3),D1(0,2,3),
A(0,0,0),F(1,2,0),B1(2,0,3),D1(0,2,3),
设E(2,y,z),则 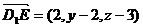
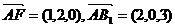 …………4分
…………4分
由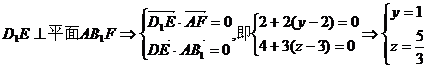
∴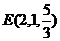 为所求 …………6分
为所求 …………6分
(Ⅱ)当D1E⊥平面AB1F时,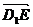 =(2,-1,
=(2,-1,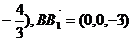 ……8分
……8分
又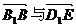 分别是平面BEF与平面B1EF的法向量, …………9分
分别是平面BEF与平面B1EF的法向量, …………9分
则二面角B1-AF-B的平面角等于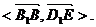 …………10分
…………10分
∵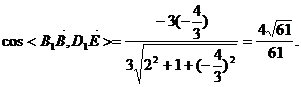 …………11分
…………11分
∴B1-AF-B的平面角为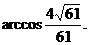
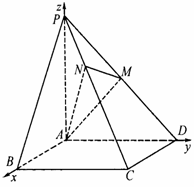
34、 (甘肃省河西五市2008年高三第一次联考)如图,已知四棱锥
(甘肃省河西五市2008年高三第一次联考)如图,已知四棱锥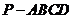 的底面是正方形,
的底面是正方形,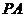 ⊥底面
⊥底面 ,且
,且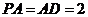 ,点
,点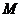 、
、 分别在侧棱
分别在侧棱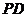 、
、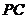 上,且
上,且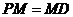

(Ⅰ)求证: ⊥平面
⊥平面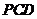 ;
;
(Ⅱ)若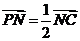 ,求平面
,求平面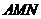 与平面
与平面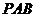 的所成锐二面角的大小
的所成锐二面角的大小
解:(Ⅰ)因为四棱锥P-ABCD的底面是正方形,PA⊥底面ABCD,
则CD⊥侧面PAD
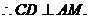 又
又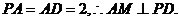
又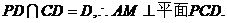 ……………5分
……………5分
(Ⅱ)建立如图所示的空间直角坐标系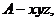 又PA=AD=2,
又PA=AD=2,
则有P(0,0,2),D(0,2,0)
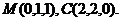
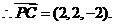
设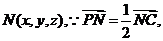 则有
则有
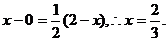
同理可得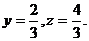
即得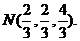 …………………………8分
…………………………8分
由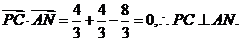

而平面PAB的法向量可为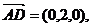
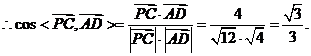
故所求平面AMN与PAB所成锐二面角的大小为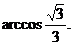
33、(福建省漳州一中2008年上期期末考试)如图所示,四棱锥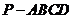 的底面为直角梯形,
的底面为直角梯形,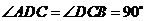 ,
,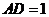 ,
,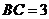 ,
,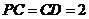 ,
,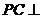 底面
底面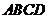 ,
,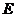 为
为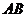 的中点.
的中点.
 (Ⅰ)求证:平面
(Ⅰ)求证:平面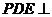 平面
平面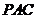 ;
;
(Ⅱ)求直线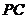 与平面
与平面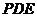 所成的角;
所成的角;
(Ⅲ)求点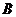 到平面
到平面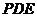 的距离.
的距离.
解法一:(Ⅰ)设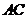 与
与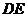 交点为
交点为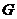 ,延长
,延长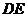 交
交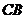 的延长线于点
的延长线于点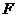 ,
,
则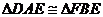 ,∴
,∴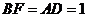 ,∴
,∴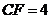 ,∴
,∴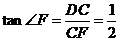 ,
,
又∵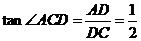 ,∴
,∴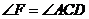 ,
,
又∵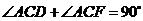 ,∴
,∴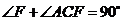 ,
,
∴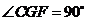 ,∴
,∴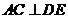
又∵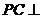 底面
底面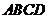 ,∴
,∴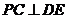 ,∴
,∴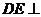 平面
平面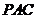 ,
,
∵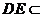 平面
平面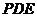 ,∴平面
,∴平面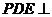 平面
平面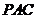 …………………………………(4分)
…………………………………(4分)
(Ⅱ)连结 ,过点
,过点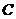 作
作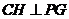 于
于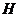 点,
点,
则由(Ⅰ)知平面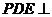 平面
平面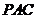 ,
,
且 是交线,根据面面垂直的性质,
是交线,根据面面垂直的性质,
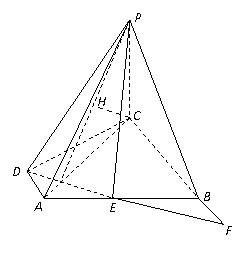 得
得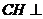 平面
平面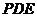 ,从而
,从而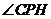 即
即
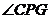 为直线
为直线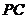 与平面
与平面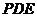 所成的角.
所成的角.
在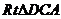 中,
中,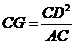
 ,
,
在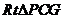 中,
中,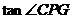
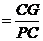
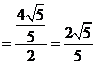 . 所以有
. 所以有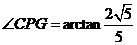 ,
,
即直线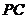 与平面
与平面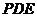 所成的角为
所成的角为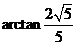 …………………………………(8分)
…………………………………(8分)
(Ⅲ)由于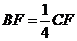 ,所以可知点
,所以可知点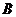 到平面
到平面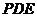 的距离等于点
的距离等于点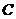 到平面
到平面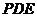 的距离的
的距离的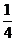 ,即
,即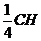 . 在
. 在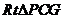 中,
中, ,
,
从而点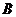 到平面
到平面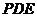 的距离等于
的距离等于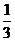 ………………………………………………(12分)
………………………………………………(12分)
解法二:如图所示,以点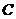 为坐标原点,
为坐标原点,
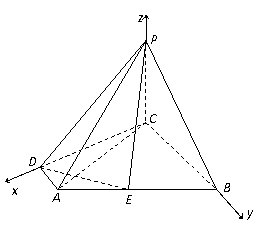 直线
直线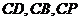 分别为
分别为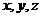 轴,
轴,
建立空间直角坐标系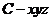 ,
,
则相关点的坐标为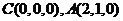
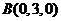 ,
,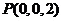 ,
,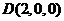 ,
,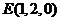 .
.
(Ⅰ)由于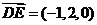 ,
,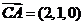 ,
,
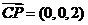 ,
,
所以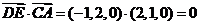 ,
,
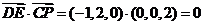 ,
,
所以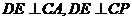 ,
,
而 ,所以
,所以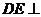 平面
平面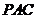 ,∵
,∵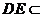 平面
平面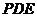 ,
,
∴平面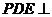 平面
平面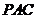 ……………………………………………………………(4分)
……………………………………………………………(4分)
(Ⅱ)设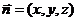 是平面
是平面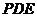 的一个法向量,则
的一个法向量,则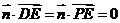 ,
,
由于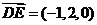 ,
,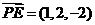 ,所以有
,所以有
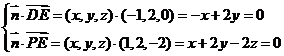 ,
,
令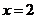 ,则
,则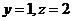 ,即
,即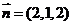 ,
,
再设直线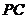 与平面
与平面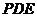 所成的角为
所成的角为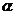 ,而
,而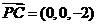 ,
,
所以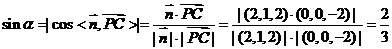 ,
,
∴ ,因此直线
,因此直线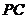 与平面
与平面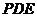 所成的角为
所成的角为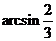 ………………(8分)
………………(8分)
(Ⅲ)由(Ⅱ)知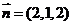 是平面
是平面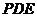 的一个法向量,而
的一个法向量,而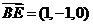 ,
,
所以点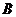 到平面
到平面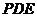 的距离为
的距离为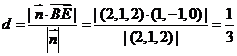
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com