
6. 下列句子中标点符号的使用,不正确的一项是 ( )
A. 在《理想国》中,柏拉图说,哲学家必须从感觉世界的“洞穴”上升到理智世界。
B. 生活中的痛苦(只要这种痛苦是真挚的。),一到了回忆中,往往也会觉得它有淡淡的甜美,化成深沉的诗。
C. 我们见到一片空虚的背景上突出地集中表现人物行动姿态,删略了背景的刻画,正像中国舞台上的表演一样。(汉画上正有不少舞蹈和戏剧表演。)
D. 知县大老爷还是原官,不过改称了什么,而且举人老爷也做了什么--这名
目,未庄人都说不明白--官,带兵的也还是先前的老把总。
5、下列各句中,语意明确、没有语病的一句是( )
A. 目前,西藏城镇职工人均每天消费蔬菜可达0.6公斤以上,讲究科学饮食的良好习惯已从城镇波及广大牧区。
B. 从神州一号到神州六号,在6年间,我国的航天技术实现了从单舱到三舱,从无人到有人,从“一人一天”到“两人五天”。
C. 寒冷,是流浪者的天敌,社会救助机构人员应在汽车站等流浪者经常出没的地方建立专门救助点,给他们发放求助单,随时同救助站取得联系。
D. 关于如何制止不良短信泛滥、防止其危害青少年的问题,一些业内人士建议,国家应设立独立部门对运营商进行监管,对短信提供商实行资质审核制。
4、下列各句中加点的成语,使用不恰当的一句是( )
A. 汉奸李某,抗战开始不久就向日寇暗送秋波,后来干脆卖身投降,公开做了日寇的走狗。
B. 我们两家是世交,有什么话不好说呢?你有什么困难,我一定鼎力相助。
C. 没有全国各族人民的共同努力,团结奋斗,全面建设小康社会的蓝图就将成为空中楼阁。
D. 陈水扁当局不把主流民意放在眼里,无节制地操弄民粹,把本来相安无事的台湾海峡两岸关系弄到剑拔弩张的地步。
3、依次填入下列各句横线处的词语,最恰当的一组是( )
(1) 某些部门人浮于事,工作________,早应该暴光,政府就应该对他们“动真格”。
(2) 俄罗斯总理弗拉德科夫将在中俄总理定期会晤中,与中方 _______旨在未来10多年时间内实现载人登月的联合太空探索计划。
(3) 现在产品的质量提高了,款式新颖了,____包装也精美了,因而更受群众欢迎。
(4) 事物的发展一旦停滞 趋于保守,就将走向灭亡, 为新生事物所代替。
A. 不力 协商 况且 或 从而
B. 不利 协商 何况 和 从而
C. 不利 商量 况且 或 而
D. 不力 商量 何况 和 而
2、下列词语中,没有错别字的一组是( )
A. 唾骂 芸芸众生 唾手可得 度假村
B. 慰藉 斩钉截铁 文过饰非 名信片
C. 驰骋 礼上往来 大有裨益 水龙头
D. 枯燥 一鳞一爪 凤毛鳞角 大拇指
1、下列词语中加点的字,注音完全正确的一组是 ( )
A. 伉俪(kàng) 不卑不亢 (kàng) 木讷(nà) 方枘圆凿(ruì)
B. 邂逅(hòu) 藏污纳垢(gòu) 连缀(zhuì) 日夜不辍(zhuì)
C. 当年(dāng) 正当权益(dàng) 蹊跷(qī) 独辟蹊径(xī)
D. 咀嚼(jué) 咬文嚼字(jiáo) 踉跄(làng) 书声琅琅(láng)
18.(本题10分)2.已知函数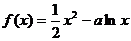
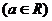 ,若函数
,若函数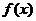 在
在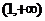 为增函数,求
为增函数,求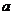 的取值范围;
的取值范围;
解:若函数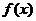 在
在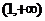 上恒成立。则
上恒成立。则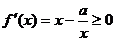 在
在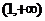 上恒成立,
上恒成立,
即: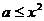 在
在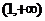 上恒成立。所以有
上恒成立。所以有
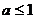
19(本题10分)已知函数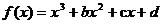 的图象过点P(0,2),且在点
的图象过点P(0,2),且在点
M(-1,f(-1))处的切线方程为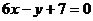 .
.
(Ⅰ)求函数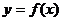 的解析式; (Ⅱ)求函数
的解析式; (Ⅱ)求函数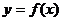 的单调区间.
的单调区间.
解:(Ⅰ)由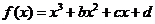 的图象过点P(0,2),d=2知,所以
的图象过点P(0,2),d=2知,所以 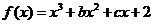 ,
,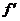 (x)=3x2+2bx+c,由在(-1,(-1))处的切线方程是6x-y+7=0,知
(x)=3x2+2bx+c,由在(-1,(-1))处的切线方程是6x-y+7=0,知
-6-f(-1)+7=0,即f(-1)=1, 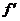 (-1)=6,∴
(-1)=6,∴ 即
即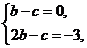 解得b=c=-3.
解得b=c=-3.
故所求的解析式为f(x)=x3-3x2-3x+2,
(Ⅱ) 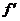 (x)=3x2-6x-3,令3x2-6x-3=0即x2-2x-1=0,解得x1=1-
(x)=3x2-6x-3,令3x2-6x-3=0即x2-2x-1=0,解得x1=1-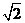 ,x2=1+
,x2=1+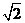 ,
,
当x<1-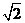 或x>1+
或x>1+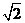 时,
时, 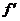 (x)>0;当1-
(x)>0;当1-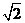 <x<1+
<x<1+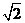 时,
时, 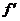 (x)<0
(x)<0
∴f(x)=x3-3x2-3x+2在(1+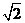 ,+∞)内是增函数,在(-∞, 1-
,+∞)内是增函数,在(-∞, 1-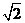 )内是增函数,在(1-
)内是增函数,在(1-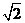 ,1+
,1+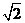 )内是减函数.
)内是减函数.
20(本题12分)已知函数f(x)=-x3+3x2+9x+a.
(I)求f(x)的单调递减区间;
(II)若f(x)在区间[-2,2]上的最大值为20,求它在该区间上的最小值.
解:(I) f ’(x)=-3x2+6x+9.令f ‘(x)<0,解得x<-1或x>3,
所以函数f(x)的单调递减区间为(-∞,-1),(3,+∞).
(II)因为f(-2)=8+12-18+a=2+a,f(2)=-8+12+18+a=22+a,
所以f(2)>f(-2).因为在(-1,3)上f ‘(x)>0,所以f(x)在[-1, 2]上单调递增,
又由于f(x)在[-2,-1]上单调递减,
因此f(2)和f(-1)分别是f(x)在区间[-2,2]上的最大值和最小值,
于是有 22+a=20,解得 a=-2.
故f(x)=-x3+3x2+9x-2,因此f(-1)=1+3-9-2=-7,
即函数f(x)在区间[-2,2]上的最小值为-7.
21(本题12分)旅游公司为3个旅游团提供4条旅游线路,每个旅游团任选其中一条.
(1)求3个旅游团选择3条不同的线路的概率
(2)求恰有2条线路没有被选择的概率.
(3)求选择甲线路旅游团数的期望.
解:(1)3个旅游团选择3条不同线路的概率为:P1=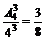
(2)恰有两条线路没有被选择的概率为:P2=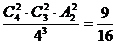
(3)设选择甲线路旅游团数为ξ,则ξ=0,1,2,3
P(ξ=0)=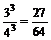 P(ξ=1)=
P(ξ=1)=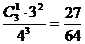
P(ξ=2)= 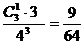 P(ξ=3)=
P(ξ=3)= 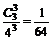
∴ξ的分布列为:
|
ξ |
0 |
1 |
2 |
3 |
|
P |
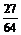 |
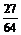 |
 |
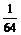
|
∴期望Eξ=0×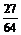 +1×
+1×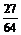 +2×
+2× +3×
+3×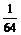 =
=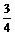
22(本题14分)4已知函数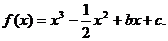
(1)若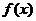 有极值,求b的取值范围;
有极值,求b的取值范围;
(2)若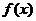 在
在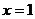 处取得极值时,当
处取得极值时,当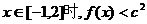 恒成立,求c的取值范围;
恒成立,求c的取值范围;
解:(1) ,
,
令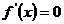 ,
,
由 得1-12b>0即
得1-12b>0即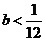
(2)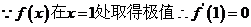 ∴3-1+b=0,得b=-2,
∴3-1+b=0,得b=-2,
令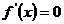 ,得
,得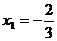 ,
,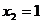 ,
,
可以计算得到 ,
,
所以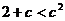 ,得到
,得到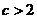 或
或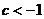
17. (本题10分)下图是容量为100的样本的频率分布直方图,试根据图形中的数据:
求(1)样本数据落在范围[6,10)内的频率.
(2)样本数据落在范围[10,14)内的频数.
(3)总体在范围[2,6)内的概率.
答:(1)0.32 (2)36 (3)0.08
15. 16. 2
13. x-y-2=0 14, 3
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com