
3.两物体的追及和相遇问题
①匀减速物体追赶同向匀速运动物体时,恰能追上或恰追不上的临界条件是即将靠近时:追赶者的速度 被追赶者的速度,当追赶者的速度大于被追赶者的速度时, 追上;当追赶者的速度小于被追赶者的速度时, 追上。
②初速度为零的匀加速运动的物体追赶同向匀速运动物体时,追上前者前两者具有最大的间距的条件是追赶者的速度 被追赶者的速度。
2.运动图象
①位移图象:纵轴表示位移s,横轴表示时间t;图线的斜率表示运动质点的速度。
②速度图象:纵轴表示速度v,横轴表示时间t;图线的斜率表示运动质点的加速度;图线与之对应的时间线所包围的面积表示位移大小;时间轴上方的面积表示正向位移,下方的面积表示负向位移,它们的代数和表示总位移。
1.匀变速直线运动的重要推论:
①某过程中间时刻的瞬时速度大小等于该过程的平均速度大小,即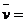
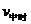 =
=
②加速度为a的匀变速直线运动在相邻的等时间T内的位移差都相等,即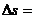 aT2。
aT2。
③物体由静止开始做匀加速直线运动的几个推论
t秒末、2t秒末、3t秒末…的速度之比为1∶2∶3∶…∶n
前t秒内、前2t秒内、前3t秒内…的位移之比为1∶4∶9∶…∶n2
第一个t秒内、第二个t秒内、第三个t秒内…的位移之比为1∶3∶5∶…∶(2n-1)
第一个s米、第二个s米、第三个s米…所用时间之比为1∶(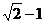 )∶(
)∶(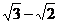 )∶…∶(
)∶…∶(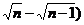
|
8.1 椭圆及其标准方程 一、复习引入 二、新课讲解 三、习题研讨 1.椭圆的定义 2.椭圆的标准方程 |
总体说明:本节课的设计力图贯彻“以人的发展为本”的教育理念,体现“教师为主导,学生为主体”的现代教学思想.在对椭圆定义的讲授中,遵循从生动直观到抽象概括的教学原则和教学途径,通过引导学生亲自动手尝试画图、发现椭圆的形成过程进而归纳出椭圆的定义,培养学生观察、辨析、归纳问题的能力;让椭圆生动灵活地呈现在学生面前,更有助于学生理解椭圆的内涵和外延.对本课另一难点标准方程推导的讲授中,在关键处设疑,以疑导思,让学生先从目的、再从方法上考虑,引导学生对比、分析,师生共同完成.通过经历椭圆方程的化简,增强了学生战胜困难的意志品质并体会数学的简洁美、对称美.通过讨论椭圆方程推导的等价性养成学生扎实严谨的科学态度.设计的例题及变式练习,充分利用新知识解决问题,使所学内容得以巩固.变式(2)的设计让学生站在方程的角度认清椭圆两种标准方程形式上的特征,将学生的思维提升到了一个新的高度.课后分层次布置作业,帮助学生巩固所学知识;课后探索更为学有余力的学生留有进一步探索、发展的空间.在教学中借助多媒体生动、直观、形象的特点来突出教学重点.自始至终很好地调动学生的积极性,挖掘他们的内在潜能,提高学生的综合素质.
|
教学 环节 |
教学内容和形式 |
设计意图 |
|
复习 提问 |
(1)
圆的定义是什么?圆的标准方程的形式怎样? (2) 如何推导圆的标准方程呢? |
激活学生已有的认知结构,为本课推导椭圆标准方程提供了方法与策略. |
|
讲授新课 |
一、授新 1. 椭圆的定义: (略) 活动过程: 操作-----交流-----归纳-----多媒体演示-----联系生活 形成概念: 操作: <1>固定一条细绳的两端,用笔尖将细绳拉紧并运动,在纸上你得到了怎样的图形? <2>如果调整 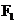 、 、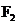 的相对位置,细绳的长度不变,猜想你的椭圆会发生怎样的变化? 的相对位置,细绳的长度不变,猜想你的椭圆会发生怎样的变化? |
在动手过程中,培养学生观察、辨析、归纳问题的能力. 在变化的过程中发现圆与椭圆的联系;建立起用联系与发展的观点看问题;为下一节深入研究方程系数的几何意义埋下伏笔. |
|
教学 环节 |
深化概念: 注:1、平面内. 2、若 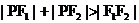 ,则点P的轨迹为椭圆. ,则点P的轨迹为椭圆.若 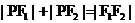 ,则点P的轨迹为线段. ,则点P的轨迹为线段.若 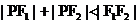 , 则点P的轨迹不存在. , 则点P的轨迹不存在.联系生活: 情境1.生活中,你见过哪些类似椭圆的图形或物体? 情境2.让学生观察倾斜的圆柱形水杯的水面边界线,并从中抽象出数学模型. (教师用多媒体演示) 情境3.观看天体运行的轨道图片. 教学内容和形式 |
准确理解椭圆的定义. 渗透数学源于生活,圆锥曲线在生产和技术中有着广泛的应用. 设计意图 |
|
|
2.椭圆的标准方程: 例:已知点 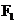 、 、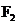 为椭圆的两个焦点,P 为椭圆上的任意一点,且 为椭圆的两个焦点,P 为椭圆上的任意一点,且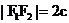 , ,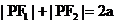 ,其中 ,其中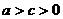 ,求椭圆的方程 ,求椭圆的方程活动过程: 点拨----- 板演 ----- 点评 一般步骤: (1) 建系设点 (2) 写出点的集合(3) 写出代数方程 (4) 化简方程 (5)证明 (4) 化简方程: <1>请一位基础较好,书写规范的同学板演 <2>教师在巡视过程中及时发现问题给予点拨 (5)证明:讨论推导的等价性 |
掌握椭圆标准方程及推导方法. 培养学生战胜困难的意志品质并感受数学的简洁美、对称美. 养成学生扎实严谨的科学态度. |
|
应用 举例 教学 环节 |
二、应用 例1.(1)椭圆 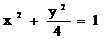 的焦点坐标为: 的焦点坐标为:
(2)椭圆 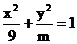 的焦距为4, 则 m 的值为: 的焦距为4, 则 m 的值为: 活动过程:思考 ----- 解答 ----- 点评 例2.已知椭圆焦点的坐标分别是(-4,0)、(4,0),椭圆上一点P到两焦点的距离的和等于10,求椭圆的标准方程 活动过程:思考 ----- 解答 ----- 点评 变式<1>已知椭圆焦点的坐标分别是(-4,0)(4,0),且经过点 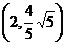 , 求椭圆的标准方程 , 求椭圆的标准方程活动过程:思考 ----- 板演 (对比) ----- 点评 教学内容和形式 |
明确椭圆两种形式的标准方程. 运用椭圆的定义,掌握椭圆的标准方程. 运用椭圆的定义或待定系数法求椭圆的标准方程. 设计意图 |
|
|
变式<2>已知椭圆经过点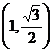 、 、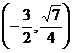 , ,求椭圆的标准方程 活动过程:思考 ----- 解答 ----- 点评 |
认清椭圆两种标准方程形式上的特征. |
|
课堂小结 |
提问:本节课学习的主要知识是什么?你学会了哪些数学思想与方法? 活动过程:教师提问 ----- 学生小结 ----- 师生补充完善 |
让学生回顾本节所学知识与方法,以逐步提高学生自我获取知识的能力. |
|
作业布置 |
作业:教材第95页,练习2、4,第96页习题8-1,1、2、3、 探索:平面内到两个定点的距离差、积、商为定值的点的轨迹是否存在?若存在轨迹是什么? |
分层次布置作业,帮助学生巩固所学知识;为学有余力的学生留有进一步探索、发展的空间. |
重点是椭圆的定义及标准方程,难点是推导椭圆的标准方程.
知识与技能目标: 准确理解椭圆的定义,掌握椭圆的标准方程及其推导.
过程与方法目标: 通过引导学生亲自动手尝试画图、发现椭圆的形成过程进而归纳出椭圆的定义,培养学生观察、辨析、归纳问题的能力.
情感、态度与价值观目标: 通过经历椭圆方程的化简,增强学生战胜困难的意志品质并体会数学的简洁美、对称美.通过讨论椭圆方程推导的等价性养成学生扎实严谨的科学态度.
假定你是李华, 你的英国朋友Peter来信向你咨询如何才能学好中文. 请你根据下列要点写回信.
要点: 1. 参加中文学习班; 2. 看中文书刊、电视; 3. 学唱中文歌曲; 4. 交中国朋友。
注意: 1.词数100左右; 2. 可适当增加细节,以使行文连贯; 3. 开头语已为你写好。
June 8, 2008
Dear Peter,
I'm glad to recerve your letter asking for my advice on how to learn Chinese well.
Best wishes,
Li Hua

75. 抱歉,我无权便宜出售它。(beyond)
_______________________________________________________________________________________
74. 我对他烦透了,因为他不停地给我打电话。(annoy)
_______________________________________________________________________________________
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com