
7.作匀加速直线运动的质点,连续两个1 s内的平均速度之差是4 m/s,在第5 s内及第6 s内的平均速度之和是56 m/s,则此质点运动的加速度为________m/s2,初速度为_________m/s.
6.一颗子弹沿水平方向射来,恰穿透三块相同的木板,设子弹穿过木板时的加速度恒定,则子弹穿过三块木板所用的时间之比为________。
5.一个物体做匀变速直线运动,若运动的时间之比为t1:t2:t3:…=1:2:3:…,下面说法中正确的是( )
A.相应的运动距离之比一定是s1:s2:s3:…=1:4:9: …
B.相邻的相同时间内的位移之比一定是s1:s2:s3:…=1:3:5: …
C.相邻的相同时间内位移之差值一定是△s=aT2,其中T为相同的时间间隔.
D.以上说法正确都是不正确的
4.一质点做匀加速直线运动,第三秒内的位移2m,第四秒内的位移是2.5m,那么以下说法中正确的是( )
A.这两秒内平均速度是2.25m/s
B.第三秒末即时速度是2.25m/s
C.质点的加速度是0.125m/s2
D.质点的加速度是0.5m/s2
3.作匀加速直线运动的质点先后经过A、B、C三点, AB = BC.质点在AB段和BC段的平均速度分别为20 m/s、30 m/s,根据以上给出的条件可以求出( )
A.质点在AC段运动的时间
B.质点的加速度
C.质点在AC段的平均速度
D.质点在C点的瞬时速度
2.对于做初速度为零的匀加速直线运动的物体,以下叙述中正确的是( ).
A.相邻的相等时间间隔内的位移之差为常数
B.相邻的相等时间间隔内的位移之差为最初的那个等时间间隔内位移的两倍
C.该物体运动过程中任意两个相等的时间间隔内速度的改变量均相等
D.该物体运动过程中任意两个相等的时间间隔内位移大小之比一定是奇数比
1.一辆车由静止开始作匀变速直线运动,在第8 s末开始刹车,经4 s停下来,汽车刹车过程也是匀变速直线运动,那么前后两段加速度的大小之比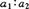 和位移之比
和位移之比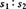 分别是( )
分别是( )
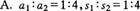
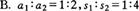
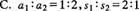
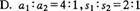
2.A、B两车相距20m,A在前B在后,沿同一方向运动,A车以2m/s的速度作匀速直线运动,B以大小为2.5m/s2的加速度作匀减速直线运动,若要B追上A,则B的初速度应满足什么条件?
1.一个初速度为6m/s做直线运动的质点,受到力F的作用,产生一个与初速度方向相反、大小为2 m/s2的加速度,当它的位移大小为3 m时,所经历的时间可能为
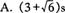
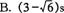
例1 有一个做匀变速直线运动的质点,它在两段连续相等的时间内通过的位移分别是24m和64m,连续相等的时间为4s,求质点的初速度和加速度大小.
[解析]依题意画草图如图1-3-1所示,用推论公式求解
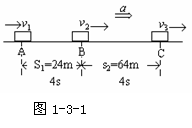 由s2-s1=aT2得64-24=a·42
由s2-s1=aT2得64-24=a·42
所以a = 2.5 m/s2,再代入s1= v1T +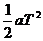
可求得 v1=1m/s.
[点评]一般的匀变速直线运动,若出现两个过程的时间相等,又知道它们的位移,用推论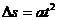 做比较方便。
做比较方便。
例2 一质点从A点开始运动,沿直线运动到B点停止,在运动过程中,物体能以 的加速度加速,也能以
的加速度加速,也能以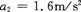 的加速度减速,也可以作匀速运动。若AB间的距离为1.6km,质点应该怎样运动,才能使它的运动时间最短,最短时间为多少?
的加速度减速,也可以作匀速运动。若AB间的距离为1.6km,质点应该怎样运动,才能使它的运动时间最短,最短时间为多少?
[解析]根据题意,质点运动方式可能有:
(1)先作一段时间匀加速运动,中间经历一段时间的匀速运动,最后作减速运动至B点速度正好为零。
(2)中间不经历匀速直线运动,先匀加速一段时间,后作匀减速运动停在B点。分别作出两种运动的 图像,如图1-3-2所示,考虑到位移相等(两斜线部分的面积应相等)。
图像,如图1-3-2所示,考虑到位移相等(两斜线部分的面积应相等)。
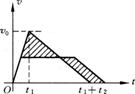
图1-3-2
从图1-3-2中容易看出第(2)种运动方式时间最短。
由图可看出,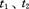 两段时间内的平均速度均为
两段时间内的平均速度均为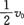 则
则
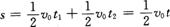 ①
①
又因为 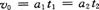 有
有
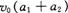
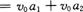
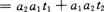
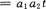
 ,代入①式
,代入①式
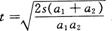
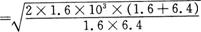
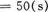
[点评]判断采用哪种运动方式,所用时间最短,也可以先建立 s与t的函数关系式,再利用极值的知识用代数方法求得。但这种解法较繁。用图线来分析解决问题,是解运动学问题的常用手段。
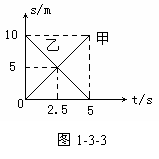
例3 甲、乙两物体的运动情况如图1-3-3所示,下列结论错误的是:
 A.甲、乙两物体的速度大小相等、方向相同
A.甲、乙两物体的速度大小相等、方向相同
B.经过2.5s的时间,甲、乙两物体相遇,相遇时它们相对
坐标原点的位移相同
C.经过5s的时间,乙物体到达甲物体的出发点
D.经过5s的时间,甲物体到达乙物体的出发点
[解析]由图中直线的斜率可求出v甲=2m/s,v乙=-2m/s,即甲、乙两物体的速度大小相等、方向相反,甲的速度方向与位移正方向相同,乙的速度方向与位移正方向相反,A错误;图中的交点表示在相同时刻两物体到达相对原点坐标相同的位置,B正确;结合坐标轴易知C、D正确,故本题应选A。
[点评]要身临其境地画出两个物体的实际运动情况,把图线转化为实际运动模型,弄清两个物体的运动情况。
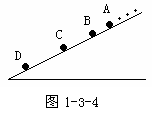 例4 相同的小球从斜面的某一位置每隔0.1s释放一颗,连续放了好几颗后,对斜面上正运动着的小球拍下部分照片,如图1-3-4所示,现测得AB=15cm,BC=20cm,已知小球在斜面上做加速度相同的匀加速直线运动(初速度为零),求:
例4 相同的小球从斜面的某一位置每隔0.1s释放一颗,连续放了好几颗后,对斜面上正运动着的小球拍下部分照片,如图1-3-4所示,现测得AB=15cm,BC=20cm,已知小球在斜面上做加速度相同的匀加速直线运动(初速度为零),求:
(1)各球的加速度的大小
(2)拍片时,A球上方正运动的球有几个?
[解析]每一个球的运动都是重复的,故对所拍的照片上的球
可认为是一个球在不同时刻的位置
由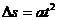 可得
可得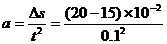 =5m/s2
=5m/s2
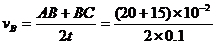 =1.75m/s
=1.75m/s
vB=at 得 t=1.75/5=0.35s,则A运动了0.25s,故在A之上有2个球
[点评]每一个推论都有较适合于某一种特定的运动模型,把许多质点的运动用一个质点来替代,能把问题转化为某种特殊的模型,对解决问题十分有用。
例5 甲、乙两车同时同地同向出发,在同一水平公路上做直线运动,甲以初速度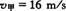 ,加速度
,加速度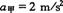 做减速运动,乙以初速度
做减速运动,乙以初速度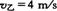 ,加速度
,加速度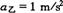 做匀加速运动.求:(1)两车再次相遇前二者间的最大距离;
做匀加速运动.求:(1)两车再次相遇前二者间的最大距离;
(2)两车再次相遇所需时间.
[解析]两车同时同地同向出发。因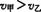 ,尽管甲作匀减速运动,乙作匀加速运动,在开始的一段时间内甲的速度大于乙的速度,两者间的距离越来越大,当甲减速,乙加速到二者速度相等时,二者间距离达到最大,此后,乙的速度大于甲的速度,二者间距离减小,当两者的位移相等时再次相遇.
,尽管甲作匀减速运动,乙作匀加速运动,在开始的一段时间内甲的速度大于乙的速度,两者间的距离越来越大,当甲减速,乙加速到二者速度相等时,二者间距离达到最大,此后,乙的速度大于甲的速度,二者间距离减小,当两者的位移相等时再次相遇.
方法1
(1)设速度相等时运动时间为t,相距最远的条件是
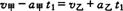
即 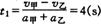
最远距离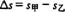
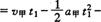
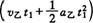
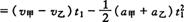
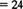
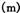
(2)设再次相遇运动时间为 ,相遇条件是
,相遇条件是
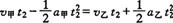
即 
代人数据整理后得 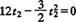
则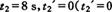 ,即是出发时刻,舍之)
,即是出发时刻,舍之)
方法2
用求二次函数的极值法解.两车间的距离
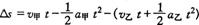
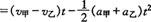
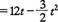
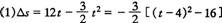 ,当t=4 s时,
,当t=4 s时, 有最大值,故最远距离
有最大值,故最远距离
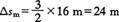
(2)当 时,两车再次相遇,即
时,两车再次相遇,即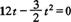
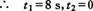 (舍去)
(舍去)
[点评]弄清追及物和被追物因速度变化而引起两者间距离变化过程,是解追及和相遇问题的关键,而两者速度相等是相距最远(或最近)的临界条件.
利用求二次函数的极值是解追及和相遇问题常用的方法,该方法的关键是找出追及物和被追物间的距离Δs关于时间t的函数关系式.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com