
1.若集合 ,则
,则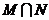 =( )
=( )
A.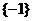 B.
B.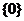 C.
C.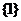 D.
D.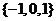
22.(14分)已知关于x的不等式+1<0的解集为空集,求实数k的取值或取值范围.
解:原不等式化为<0.
(1)若1-k>0即k<1时,
不等式等价于(x-)(x-2)<0.
①若k<0,不等式的解集为{x|<x<2}.
②若k=0,不等式的解集为Ø
③若0<k<1,不等式的解集为{x|2<x<}.
(2)若1-k<0即k>1时,
不等式等价于(x-)(x-2)>0.
此时恒有2>,
所以不等式解集为{x|x<,或x>2}.
综上可知当且仅当k=0时,不等式的解集为空集.
21.(12分)设函数f(x)=-4x+b,且不等式|f(x)|<c的解集为{x|-1<x<2}.
(1)求b的值;
(2)解关于x的不等式(4x+m)f(x)>0(m∈R).
解:(1)由|-4x+b|<c得<x<,
|f(x)|<c⇔{x|-1<x<2},
则,∴,故b=2.
(2)f(x)=-4x+2,则(4x+m)(2-4x)>0,
即(4x+m)(4x-2)<0.
当->,即m<-2时,<x<-;
当-=,即m=-2时,不等式无解;
当-<,即m>-2时,-<x<.
综上,当m<-2时,解集为(,-);
当m=-2时,解集为Ø;
当m>-2时,解集为(-,).
20.(12分)已知命题p:x2+mx+1=0有两个不相等的负数根;命题q:方程4x2+4(m-2)x+1=0无实根,若“p或q”为真,而“p且q”为假,求实数m的取值范围.
解:命题p为真时,所以m>2.
命题q为真时,Δ=[4(m-2)]2-4×4×1<0,即1<m<3.
又∵“p或q”为真“p且q”为假,∴p,q必为一真一假,
若p真q假,则m≥3,
若p假q真,则1<m≤2.
∴实数m的取值范围为(1,2]∪[3,+∞).
19.(12分)已知不等式组的解集是不等式2x2-9x+a<0的解集的子集,求实数a的取值范围.
解:解不等式组⇒{x|2<x<3}.
由于{x|2<x<3}是2x2-9x+a<0的解集的子集,等价不等式2x2-9x+a<0在(2,3)上恒成立,
令f(x)=2x2-9x+a,则⇒a∈(-∞,9].
∴实数a的取值范围为(-∞,9].
18.(12分)解下列含绝对值的不等式:
(1)1<|x-2|≤3;
(2)|x+2|≥|x|;
(3)|x+2|>|x-1|-3.
解:(1)对于此双向不等式可化为
⇒
∴原不等式的解集为{x|-1≤x<1或3<x≤5}.
(2)将不等式两边平方得(x+2)2≥x2,∴x≥-1,
即原不等式的解集为{x|x≥-1}.
(3)分别令x+2=0及x-1=0得x=-2与x=1.
当x∈(-∞,-2)时,有-(x+2)>-(x-1)-3,无解;
当x∈[-2,1)时,有x+2>-(x-1)-3,
解得-2<x<1;
当x∈[1,+∞)时,有x+2>x-1-3,解得x≥1.
综上知:原不等式的解集为{x|x>-2}.
17.(12分)(1)写出命题“末位数字是0或5的整数能被5整除”的否命题及命题的否定形式(非p形式);
(2)求使函数y=(a2+4a-5)x2-4(a-1)x+3的图象全在x轴上方的充分必要条件.
解:(1)命题的否定:末位数字是0或5的整数,不能被5整除.否命题:末位数字不是0也不是5的整数,不能被5整除.
(2)由
解得1<a<19,
由a=1时符合条件,所以1≤a<19为所求.
16.(2009·吉林检测)给出下面四个命题:
①m=3是直线(m+3)x+my-2=0与直线mx-6y+5=0互相垂直的充要条件;
②b=是a,b,c三个数成等比数列的既不充分又不必要条件;
③函数y=f(x)存在反函数是y=f(x)为单调函数的充要条件;
④两个向量相等是这两个向量共线的充分不必要条件.
其中真命题的序号是________(写出所有真命题的序号).
解析:①:(m+3)x+my-2=0与mx-6y+5=0垂直
⇔(m+3)m-6m=0
⇔m=0或m=3,∴①错.
③:存在反函数但不一定单调
例如:y=,所以③错.
答案:②④
15.(2009·衡阳联考)对于两个非空集合M、P,定义运算:M⊗P={x|x∈M,x∈P,且x∉M∩P}.已知集合A={x|x2-3x+2=0},B={y|y=x2-2x+3,x∈A},则A⊗B=__________.
解析:依题意易得A={1,2},B={2,3},A⊗B={1,3}.
答案:{1,3}
14.已知集合A={x|x2+x-6=0},B={x|mx+1=0},若B⊆A,则m的值为__________.
解析:由题意知,A={x|x2+x-6=0}={-3,2},
因为B⊆A,所以若mx+1=0有解,则解为-3或2,
当x=-3时,m=;
当x=2时,m=-.
若mx+1=0无解,则m=0.
故m的值为或-或0.
答案:或-或0
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com