
A组 2010年高考题
14.
(1)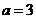 时,
时,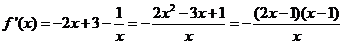 ,
,
函数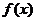 在区间
在区间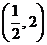 仅有极大值点
仅有极大值点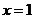 ,故这个极大值点也是最大值点,
,故这个极大值点也是最大值点,
故函数在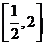 最大值是
最大值是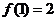 ,
,
又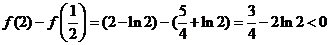 ,故
,故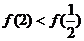 ,
,
故函数在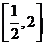 上的最小值为
上的最小值为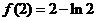 。(4分)
。(4分)
(2)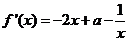 ,令
,令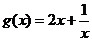 ,则
,则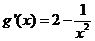 ,
,
则函数在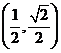 递减,在
递减,在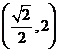 递增,由
递增,由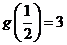 ,
,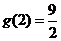 ,
,
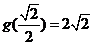 ,故函数
,故函数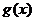 在
在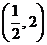 的值域为
的值域为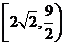 。
。
若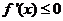 在
在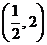 恒成立,即
恒成立,即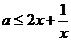 在
在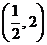 恒成立,
恒成立,
只要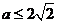 ,若要
,若要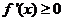 在在
在在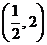 恒成立,即
恒成立,即 在
在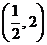 恒成立,
恒成立,
只要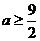 。即
。即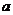 的取值范围是
的取值范围是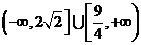 。(8分)
。(8分)
(3)若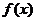 既有极大值又有极小值,则首先必须
既有极大值又有极小值,则首先必须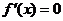 有两个不同正根
有两个不同正根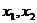 ,
,
即 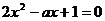 有两个不同正根。
有两个不同正根。
故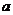 应满足
应满足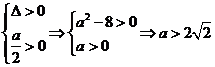 ,∴当
,∴当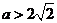 时,
时,
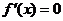 有两个不等的正根,不妨设
有两个不等的正根,不妨设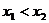 ,
,
由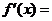
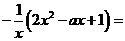
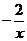
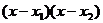 知:
知: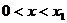 时
时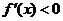 ,
,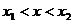 时
时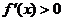 ,
,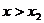 时
时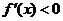 ,
,
∴当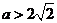 时
时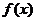 既有极大值
既有极大值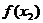 又有极小值
又有极小值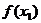 .
.
反之,当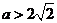 时,
时,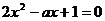 有两个不相等的正根,故函数
有两个不相等的正根,故函数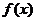 既有极大值又有极小值的充要条件
既有极大值又有极小值的充要条件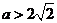 。 (12分)
。 (12分)
13. (1)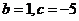 ;…………(3分)
;…………(3分)
(2)假设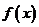 图像在
图像在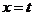 处的切线与直线
处的切线与直线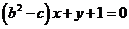 平行,
平行,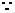
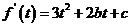 ,直线
,直线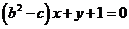 的斜率为
的斜率为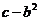 ,
,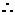
 ,即
,即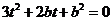 ,
,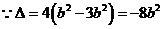 ,又
,又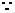
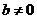 ,
,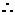
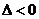 .从而
.从而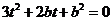 无解,因此不存在
无解,因此不存在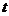 ,使
,使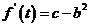 ,故
,故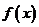 图像不存在与直线
图像不存在与直线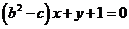 平行的切线.…………(8分)
平行的切线.…………(8分)
(3)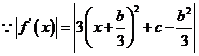 ,
,
①若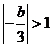 ,即
,即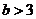 或
或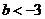 时,M应为
时,M应为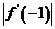 与
与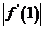 中最大的一个,
中最大的一个,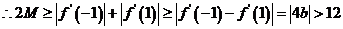 ,
,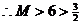 …………(10分)
…………(10分)
②若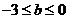 时,
时, 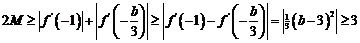 ,
, ……(12分)
……(12分)
③若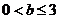 时,
时, 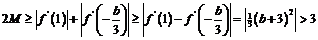 ,
,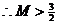
综上,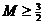 …………(14分)
…………(14分)
法二: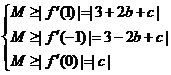

∴M≥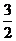
12. 解:(1)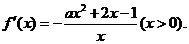
依题意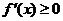 在
在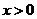 时恒成立,即
时恒成立,即 在
在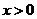 恒成立.
恒成立.
则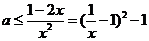 在
在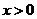 恒成立,
恒成立,
即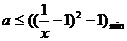
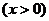
当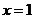 时,
时,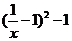 取最小值
取最小值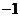
∴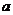 的取值范围是
的取值范围是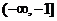 ……
……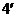
(2)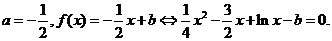
设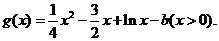 则
则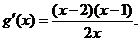 列表:
列表:
 |
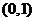 |
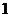 |
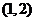 |
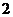 |
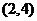 |
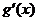 |
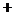 |
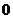 |
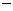 |
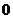 |
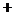 |
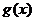 |
|
极大值 |
¯ |
极小值 |
|
∴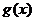 极小值
极小值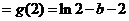 ,
,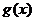 极大值
极大值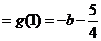 ,
,
又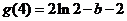 ……
……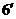
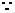 方程
方程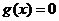 在[1,4]上恰有两个不相等的实数根.
在[1,4]上恰有两个不相等的实数根.
则 , 得
, 得
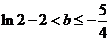 …………
…………
(3)设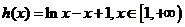 ,则
,则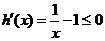
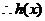 在
在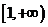 为减函数,且
为减函数,且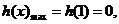 故当
故当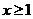 时有
时有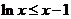 .
.
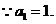 假设
假设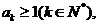 则
则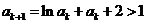 ,故
,故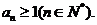
从而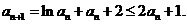
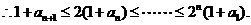
即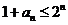 ,∴
,∴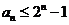 …………
…………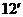
11.( 1)当 时,
时,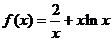 ,
,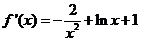 ,
,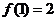 ,
, ,
,
所以曲线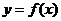 在
在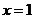 处的切线方程为
处的切线方程为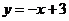 ;
;
(2)存在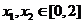 ,使得
,使得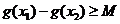 成立,等价于:
成立,等价于: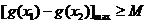 ,
,
考察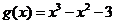 ,
, ,
,
|
|
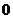 |
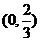 |
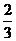 |
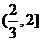 |
2 |
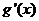 |
|
- |
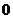 |
+ |
|
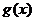 |
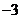 |
递减 |
极小值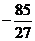 |
递增 |
1 |
由上表可知: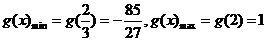 ,
,
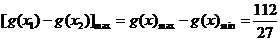 ,
,
所以满足条件的最大整数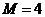 ;
;
(3)对任意的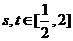 ,都有
,都有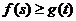 成立
成立
等价于:在区间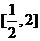 上,函数
上,函数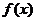 的最小值不小于
的最小值不小于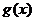 的最大值,
的最大值,
由(2)知,在区间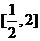 上,
上,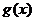 的最大值为
的最大值为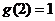 。
。
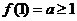 ,下证当
,下证当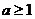 时,在区间
时,在区间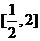 上,函数
上,函数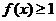 恒成立。
恒成立。
当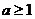 且
且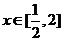 时,
时,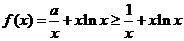 ,
,
记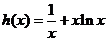 ,
,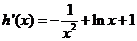 ,
, 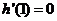 。
。
当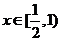 ,
,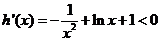 ;当
;当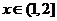 ,
,
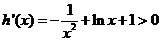 ,
,
所以函数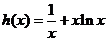 在区间
在区间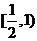 上递减,在区间
上递减,在区间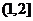 上递增,
上递增,
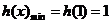 ,即
,即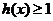 ,
所以当
,
所以当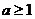 且
且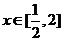 时,
时,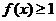 成立,
成立,
即对任意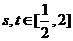 ,都有
,都有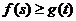 。
。
(3)另解:当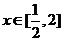 时,
时,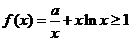 恒成立
恒成立
等价于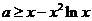 恒成立,记
恒成立,记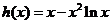 ,
,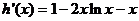 ,
, 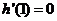 。
。
记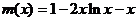 ,
,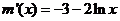 ,由于
,由于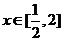 ,
,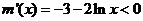 , 所以
, 所以 在
在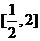 上递减,当
上递减,当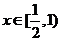 时,
时,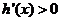 ,
,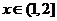 时,
时,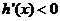 ,即函数
,即函数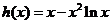 在区间
在区间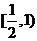 上递增,在区间
上递增,在区间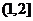 上递减,所以
上递减,所以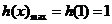 ,所以
,所以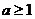 .
.
10. (1)解法1:∵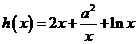 ,其定义域为
,其定义域为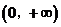 ,
,
∴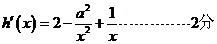 .
.
∵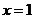 是函数
是函数 的极值点,∴
的极值点,∴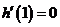 ,即
,即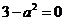 .
.
∵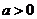 ,∴
,∴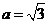 .
.
经检验当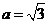 时,
时,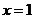 是函数
是函数 的极值点,
的极值点,
∴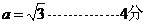 .
.
解法2:∵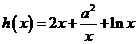 ,其定义域为
,其定义域为 ,
,
∴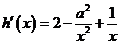 .
.
令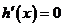 ,即
,即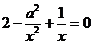 ,整理,得
,整理,得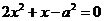 .
.
∵ ,
,
∴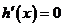 的两个实根
的两个实根 (舍去),
(舍去),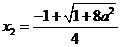 ,……2分
,……2分
当 变化时,
变化时, ,
,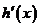 的变化情况如下表:
的变化情况如下表:
 |
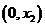 |
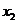 |
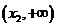 |
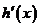 |
- |
0 |
+ |
 |
减 |
极小值 |
增 |
依题意,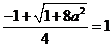 ,即
,即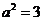 ,
,
∵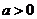 ,∴
,∴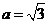 .………… 4分
.………… 4分
(2)解:对任意的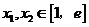 都有
都有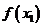 ≥
≥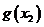 成立等价于对任意的
成立等价于对任意的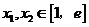 都有
都有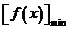 ≥
≥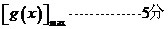 .
.
当
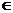 [1,
[1,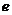 ]时,
]时,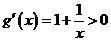 .
.
∴函数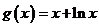 在
在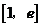 上是增函数.
上是增函数.
∴ .
.
∵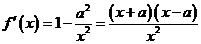 ,且
,且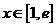 ,
,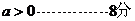 .
.
①当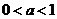 且
且
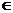 [1,
[1,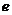 ]时,
]时,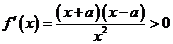 ,
,
∴函数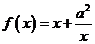 在[1,
在[1,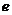 ]上是增函数,
]上是增函数,
∴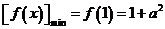 .
.
由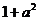 ≥
≥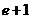 ,得
,得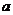 ≥
≥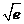 ,
,
又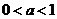 ,∴
,∴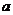 不合题意.
不合题意.
②当1≤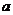 ≤
≤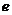 时,
时,
若1≤ <
<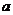 ,则
,则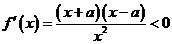 ,
,
若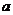 <
< ≤
≤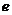 ,则
,则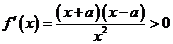 .
.
∴函数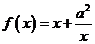 在
在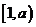 上是减函数,在
上是减函数,在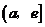 上是增函数.
上是增函数.
∴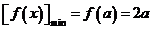 .
.
由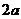 ≥
≥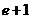 ,得
,得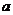 ≥
≥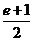 ,
,
又1≤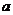 ≤
≤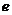 ,∴
,∴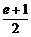 ≤
≤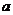 ≤
≤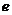 .
. 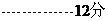
③当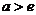 且
且
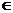 [1,
[1,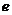 ]时,
]时,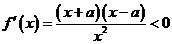 ,
,
∴函数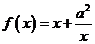 在
在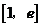 上是减函数.
上是减函数.
∴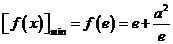 .
.
由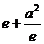 ≥
≥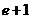 ,得
,得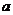 ≥
≥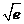 ,
,
又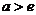 ,∴
,∴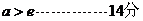 .
.
综上所述,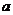 的取值范围为
的取值范围为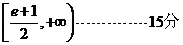 .
.
9. 解:(1)由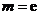 得
得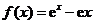 ,
,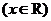 ,所以
,所以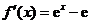 .
.
由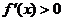 得
得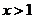 ,∴
,∴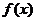 的单调递增区间是
的单调递增区间是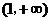 ;
;
由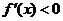 得
得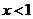 ,∴
,∴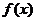 的单调递减区间是
的单调递减区间是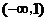 .
…………4分
.
…………4分
(2)由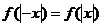 可知
可知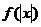 是偶函数.于是
是偶函数.于是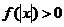 对任意
对任意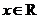 恒成立,
恒成立,
等价于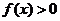 对任意
对任意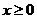 恒成立.
恒成立.
①当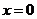 时,
时,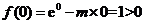 恒成立;
恒成立;
②当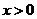 时,由
时,由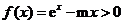 得
得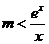 ,设
,设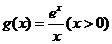 ,则
,则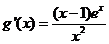
由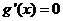 得
得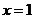 .
.
当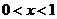 时,
时,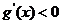 ,
,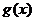 是递减函数;
是递减函数;
当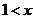 时,
时,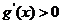 ,
,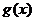 是递增函数;∴
是递增函数;∴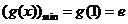 ,∴
,∴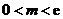 .
.
综合上可得,实数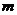 的取值范围是
的取值范围是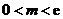 .
…………9分
.
…………9分
(3)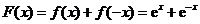 ,
,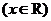 .显然,
.显然,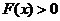 .
.
∴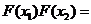
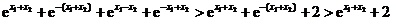 ,
,
∴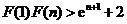 ,
,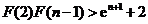 ,…………,
,…………,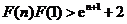 .
.
由此得, …
…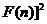
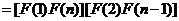 …
…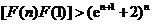 .
.
故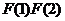 …
…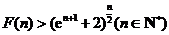 .
…………14分
.
…………14分
8. (Ⅰ)解: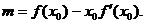 …………………………………………2分
…………………………………………2分
(Ⅱ)证明:令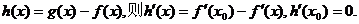
因为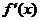 递减,所以
递减,所以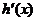 递增,因此,当
递增,因此,当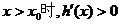 ;
;
当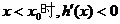 .所以
.所以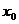 是
是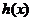 唯一的极值点,且是极小值点,可知
唯一的极值点,且是极小值点,可知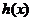 的
的
最小值为0,因此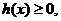 即
即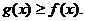 …………………………7分
…………………………7分
(Ⅲ)解法一: ,
,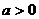 是不等式成立的必要条件,以下讨论设此条件成立.
是不等式成立的必要条件,以下讨论设此条件成立.
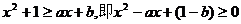 对任意
对任意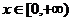 成立的充要条件是
成立的充要条件是
 …………………………10分
…………………………10分
另一方面,由于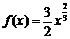 满足前述题设中关于函数
满足前述题设中关于函数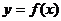 的条件,利用(II)的结果可知,
的条件,利用(II)的结果可知,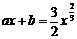 的充要条件是:过点(0,
的充要条件是:过点(0,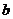 )与曲线
)与曲线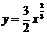 相切的直线的斜率大于
相切的直线的斜率大于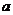 ,该切线的方程为
,该切线的方程为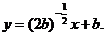
于是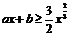 的充要条件是
的充要条件是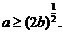 …………………………12分
…………………………12分
综上,不等式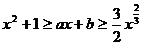 对任意
对任意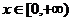 成立的充要条件是
成立的充要条件是
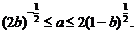 ①
①
显然,存在a、b使①式成立的充要条件是:不等式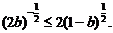 ②
②
有解、解不等式②得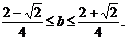 ③
③
因此,③式即为b的取值范围,①式即为实数在a与b所满足的关系.…………15分
7. 解:(I)设函数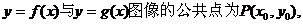 则有
则有

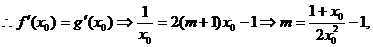 ②
②
②代入①,得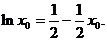
设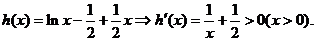
所以,函数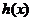 最多只有1个零点,
最多只有1个零点,
观察得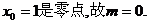 …………4分
…………4分
此时,点P(1,0)。 ………………5分
(II)根据(I)知,当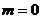 时,两条曲线切于点P(1,0),
时,两条曲线切于点P(1,0),
此时,变化的
而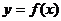 是固定不变的,如果继续让对称轴向右移动,
是固定不变的,如果继续让对称轴向右移动,
即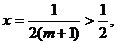
解得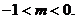 ………………9分
………………9分
两条曲线有两个不同的交点,当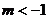 时,开口向下,
时,开口向下,
只有一个交点,显然不合题意,
所以,有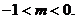 ………………10分
………………10分
(III)假设存在这样的m,不妨设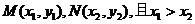
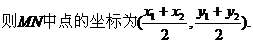
以S为切线的切线l1的斜率
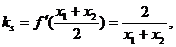
以T为切点的切线l2的斜率
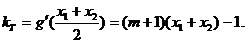
如果存在m,使得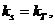
即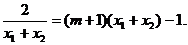 ③
③
而且有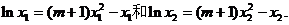
如果将③的两边同乘以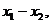 得
得
|
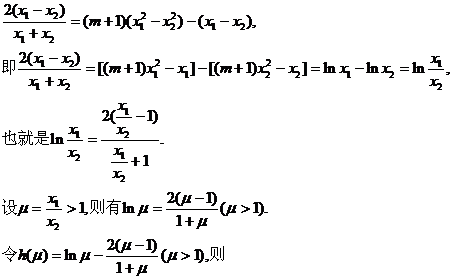
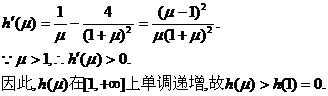
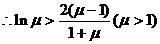 ⑤
⑤
∴④与⑤矛盾。
所以,不存在实数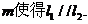 ………………15分
………………15分
6. ⑴当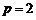 时,函数
时,函数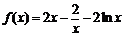 ,
,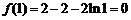 .
.
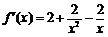 ,
,
曲线 在点
在点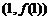 处的切线的斜率为
处的切线的斜率为 .
.
从而曲线 在点
在点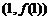 处的切线方程为
处的切线方程为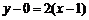 ,
,
即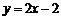 .
.
⑵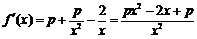 .
.
令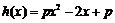 ,要使
,要使 在定义域
在定义域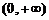 内是增函数,只需
内是增函数,只需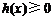 在
在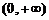 内恒成立.
内恒成立.
由题意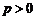 ,
,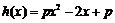 的图象为开口向上的抛物线,对称轴方程为
的图象为开口向上的抛物线,对称轴方程为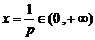 ,∴
,∴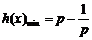 ,
,
只需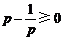 ,即
,即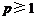 时,
时,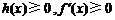
∴ 在
在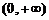 内为增函数,正实数
内为增函数,正实数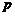 的取值范围是
的取值范围是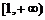 .
.
⑶∵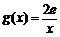 在
在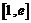 上是减函数,
上是减函数,
∴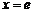 时,
时,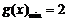 ;
;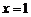 时,
时,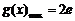 ,即
,即 ,
,
①当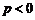 时,
时,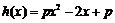 ,其图象为开口向下的抛物线,对称轴
,其图象为开口向下的抛物线,对称轴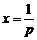 在
在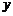 轴的左侧,且
轴的左侧,且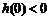 ,所以
,所以 在
在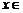
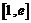 内是减函数.
内是减函数.
当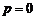 时,
时,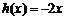 ,因为
,因为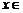
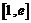 ,所以
,所以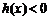 ,
,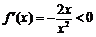 ,
,
此时, 在
在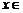
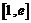 内是减函数.
内是减函数.
故当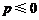 时,
时, 在
在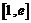 上单调递减
上单调递减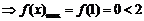 ,不合题意;
,不合题意;
②当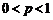 时,由
时,由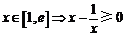 ,
,
所以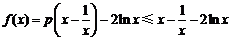 .
.
又由⑵知当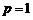 时,
时, 在
在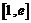 上是增函数,
上是增函数,
∴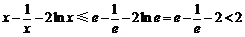 ,不合题意;
,不合题意;
③当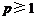 时,由⑵知
时,由⑵知 在
在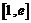 上是增函数,
上是增函数,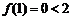 ,
,
又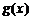 在
在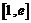 上是减函数,
上是减函数,
故只需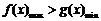 ,
,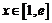 ,
,
而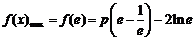 ,
,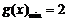 ,
,
即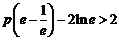 ,解得
,解得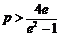 ,
,
所以实数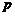 的取值范围是
的取值范围是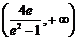 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com