
11、(9分)某同学利用打点计时器所记录的纸带,来研究做匀变速直线运动小车的运动情况,实验中获得一条纸带,如图所示,各计数点中间还有4个点没有画出来,已知所用电源的频率为50HZ,测得x1=3.18cm,x2=6.75cm,x3=10.70cm,x4=15.05cm,,则在打B点时小车的速度为VB=_____________;小车运动的加速度表达式为a=_______________;代入数据后算出加速度大小为___________________。(计算结果保留三位有效数字)。

O A B C D




 · ·
·
·
·
· ·
·
·
·
 x1
x1
 x2
x2

x3

x4
20、(本大题满分16分)
解:(1)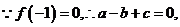
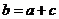
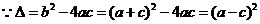 当
当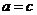 时
时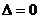 ,
,
函数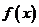 有一个零点;当
有一个零点;当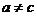 时,
时,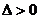 ,函数
,函数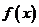 有两个零点。………4分
有两个零点。………4分
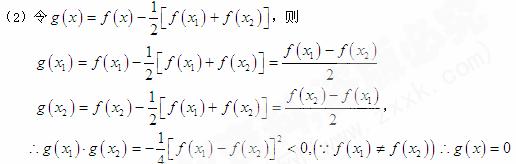
在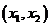 内必有一个实根。即
内必有一个实根。即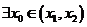 ,使
,使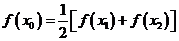 成立。
成立。
………………10分
(3)假设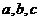 存在,由①知抛物线的对称轴为x=-1,且
存在,由①知抛物线的对称轴为x=-1,且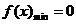
∴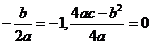
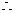
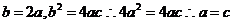
由②知对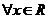 ,都有
,都有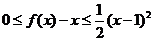
令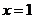 得
得
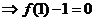
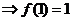
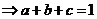 ……………13分
……………13分
由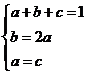 得
得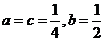 , ………………………………………………15分
, ………………………………………………15分
当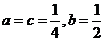 时,
时,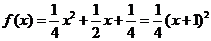 ,其顶点为(-1,0)满足条件①,又
,其顶点为(-1,0)满足条件①,又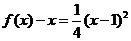
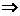 对
对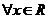 ,都有
,都有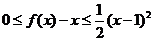 ,满足条件②。∴存在
,满足条件②。∴存在 ,使
,使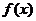 同时满足条件①、②。…………………………16分
同时满足条件①、②。…………………………16分
19、(本大题满分16分)
(Ⅰ)∵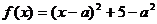 (
(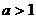 ),∴
),∴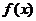 在
在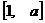 上是减函数,
上是减函数,
又定义域和值域均为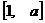 ,∴
,∴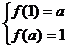 , 即
, 即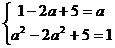 ,
解得
,
解得 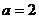 .
.
(II) ∵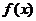 在区间
在区间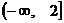 上是减函数,∴
上是减函数,∴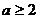 ,
,
又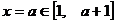 ,且,
,且,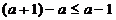
∴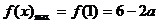 ,
,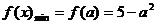 .
.
∵对任意的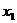 ,
,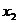
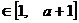 ,总有
,总有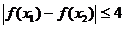 ,
,
∴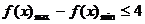 ,
, .
.
18、(本大题满分16分)
解:(1)由题意,得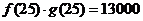 ,即
,即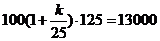 ,解得
,解得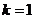 ……3分
……3分
(2)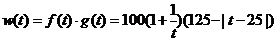
=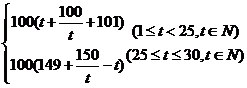
(3)①当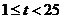 时,因为
时,因为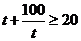 ,所以当
,所以当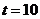 时,
时,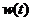 有最小值12100
有最小值12100
②当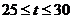 时,∵
时,∵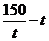 在
在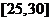 上递减,∴当
上递减,∴当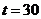 时,
时,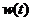 有最小值12400
有最小值12400
∵12100〈12400,∴当 时,该商品的日销售金额
时,该商品的日销售金额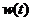 取得最小值为12100
取得最小值为12100
17、(本大题满分14分)
解:(1)当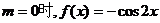 , ………………2分
, ………………2分
令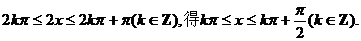
因此 …………6分
…………6分
(2)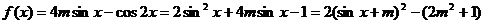
………………8分
令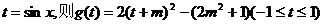 。
。
①若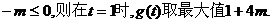
由 ; ………………12分
; ………………12分
②若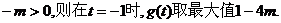
由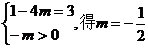 ; ………………16分
; ………………16分
综上,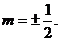
16、(本大题满分14分)
解:(1)因为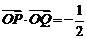 ,所以
,所以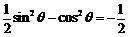 ,
,
即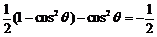 ,所以
,所以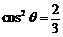 ,
,
所以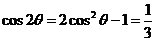 .
.
(2)因为 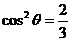 ,所以
,所以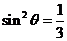 ,所以
,所以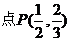 ,
,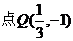 ,
,
又点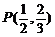 在角
在角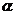 的终边上,所以
的终边上,所以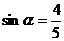 ,
,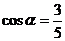 .
.
同理 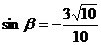 ,
,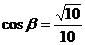 ,
,
所以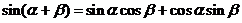
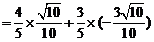
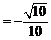 .
.
15、(本大题满分14分)
解:(Ⅰ)设等差数列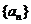 的公差
的公差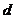 。
。
因为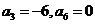
所以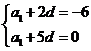 解得
解得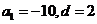
所以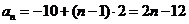
(Ⅱ)设等比数列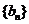 的公比为
的公比为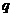
因为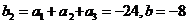
所以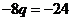 即
即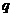 =3
=3
所以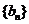 的前
的前 项和公式为
项和公式为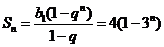
20.已知二次函数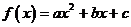 .
.
(1)若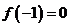 ,试判断函数
,试判断函数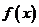 零点个数;
零点个数;
(2)若对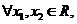 且
且 ,
,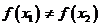 ,试证明
,试证明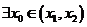 ,使
,使
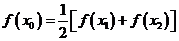 成立;
成立;
(3)是否存在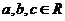 ,使
,使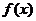 同时满足以下条件①对
同时满足以下条件①对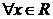 ,
,
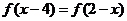 ,且
,且 ;②对
;②对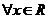 ,都有
,都有
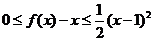 .若存在,求出
.若存在,求出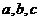 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.

19.已知函数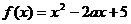 (
( ).
).
(I)若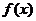 的定义域和值域均是
的定义域和值域均是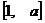 ,求实数
,求实数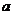 的值;
的值;
(II)若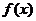 在区间
在区间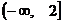 上是减函数,且对任意的
上是减函数,且对任意的 ,
,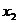
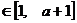 ,总有
,总有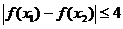 ,求实数
,求实数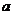 的取值范围.
的取值范围.
18.经市场调查,某商场的一种商品在过去的一个月内(以30天计)销售价格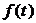 (元)与时间
(元)与时间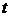 (天)的函数关系近似满足
(天)的函数关系近似满足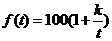 (
(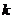 为正常数),日销售量
为正常数),日销售量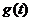 (件)与时间
(件)与时间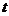 (天)的函数关系近似满足
(天)的函数关系近似满足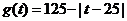 ,且第25天的销售金额为13000元.
,且第25天的销售金额为13000元.
(1)求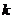 的值;
的值;
(2)试写出该商品的日销售金额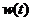 关于时间
关于时间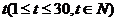 的函数关系式;
的函数关系式;
(3)该商品的日销售金额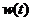 的最小值是多少?.
的最小值是多少?.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com