
1.组合的概念:一般地,从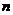 个不同元素中取出
个不同元素中取出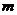
 个元素并成一组,叫做从
个元素并成一组,叫做从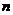 个不同元素中取出
个不同元素中取出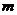 个元素的一个组合
个元素的一个组合
2.掌握组合数计算公式和组合数的性质,能解决一些简单的应用问题
1.理解组合的意义,能正确区分排列与组合;
21. (本小题满分14分)选修4-5:不等式选讲
(Ⅰ)设函数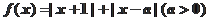 .若不等式
.若不等式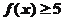 的
的
解集为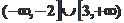 ,求
,求 的值.
21世纪教育网
的值.
21世纪教育网
(Ⅱ)如图,O为数轴的原点,A,B,M为数轴上三点,C为线段OM上的动点,设x表示C与原点的距离,y 表示C到A距离4倍与C道B距离的6倍的和.
(1)将y表示成x的函数;
(2)要使y的值不超过70,x 应该在什么范围内取值?

20. (本小题满分14分)
(本小题满分14分)
如图,有一块矩形空地,要在这块空地上辟一个内接四边形为绿地,使其四个顶点分别落在矩形的四条边上,已知AB= (
(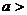 2),BC=2,且AE=AH=CF=CG,设AE=
2),BC=2,且AE=AH=CF=CG,设AE=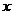 ,绿地面积为
,绿地面积为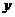 . 21世纪教育网
. 21世纪教育网
(Ⅰ)写出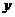 关于
关于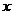 的函数关系式,并指出这个函数的定义域.
的函数关系式,并指出这个函数的定义域.
(Ⅱ)当AE为何值时,绿地面积最大?
19. (本小题满分13分)
(Ⅰ) 设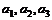 均为正数,且
均为正数,且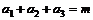 ,求证
,求证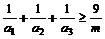 .
.
(Ⅱ) 求函数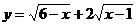 的最大值21世纪教育网
的最大值21世纪教育网
18. (本小题满分13分)
(Ⅰ) 已知不等式 的解集是
的解集是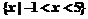
解不等式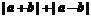 ≥
≥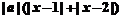 21世纪教育网
21世纪教育网
(Ⅱ)设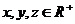 ,且x+2y+3z=36,求
,且x+2y+3z=36,求 的最小值.
的最小值.
17.(本小题满分13分)
已知命题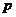 :方程
:方程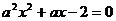 在[-1,1]上有解;命题
在[-1,1]上有解;命题 :只有一个实数
:只有一个实数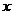 满足不等式
满足不等式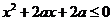 ,若命题“p或q”是假命题,求实数a的取值范围. 21世纪教育网
,若命题“p或q”是假命题,求实数a的取值范围. 21世纪教育网
16. (本小题满分13分)21世纪教育网
记函数 的定义域为
的定义域为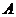 ,
,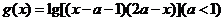 的
的
定义域为B.
(Ⅰ)求集合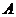 ;
;
(Ⅱ)若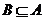 , 求实数
, 求实数 的取值范围.
的取值范围.
15.设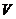 是已知平面
是已知平面 上所有向量的集合,对于映射
上所有向量的集合,对于映射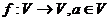 ,记
,记 的象为
的象为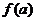 。若映射
。若映射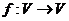 满足:对所有
满足:对所有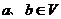 及任意实数
及任意实数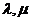 都有
都有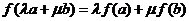 ,则
,则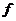 称为平面
称为平面 上的线性变换。现有下列命题:
上的线性变换。现有下列命题:
①设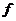 是平面
是平面 上的线性变换,
上的线性变换,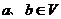 ,则
,则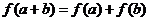
②若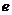 是平面
是平面 上的单位向量,对
上的单位向量,对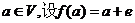 ,则
,则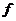 是平面
是平面 上的线性变换;
上的线性变换;
③对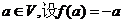 ,则
,则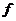 是平面
是平面 上的线性变换;
上的线性变换;
④设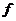 是平面
是平面 上的线性变换,
上的线性变换, ,则对任意实数
,则对任意实数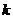 均有
均有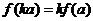 。
。
其中的真命题是 (写出所有真命题的编号)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com