
3.(2006天津)将4个颜色互不相同的球全部放入编号为1和2的两个盒子里,使得放入每个盒子里的球的个数不小于该盒子的编号,则不同的放球方法有 ( )
A.10种 B.20种 C.36种 D.52种
2.(2004江苏)从4名男生和3名女生中选出4人参加某个座谈会,若这4人中必须既有男生又有女生,则不同的选法共有 ( )
A.140种 B.120种 C.35种 D.34种
1.从6双不同颜色的手套中任取4只,其中恰好有一双同色的取法有 ( )
A.240种 B.180种 C.120种 D.60种
3.排列与组合的联系
同步练习 10.2 组合
[选择题]
2.带限制条件的组合问题.
1.组合的概念,组合数的公式和性质:
[例1]求值:(1)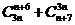 ; (2)
; (2)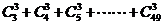
解(1)由组合定义知:
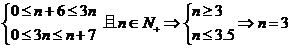
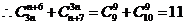 .
.
(2) 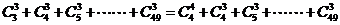
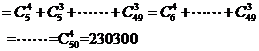
◆ 特别提示:排列组合中对n,m的限制。
[例2]用正五棱柱的10个顶点中的5个做四棱锥的5个顶点,共可得到多少个四棱锥?
解:解法1 直接法:共面而不共线的四点可成为四棱锥的底面,再在平面外找一点为顶点就形成了四棱锥,于是可从四棱锥的底面四点着眼,将构成棱锥的5个顶点的取法分类。
按照构成四棱锥的底面四点分为以下四类;
(1)四点取在棱柱的底面上有2C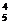 C
C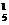 =50个;
=50个;
(2)四点取在棱柱的侧面上有5C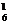 =30个;
=30个;
(3)四点取在棱柱的对角面上有5C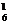 =30个;
=30个;
(4)四点取在以过一个底面中的一条对角线和另一个底面中与其平行的一边所确定的面上有2×5C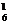 =60个。
=60个。
所以共可组成50+30+30+60=170个四棱锥。
解法2 间接法. C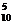 中去掉五点共面和无四点共面的两种情况,算式为C
中去掉五点共面和无四点共面的两种情况,算式为C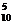 -2C
-2C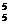 -4×4C
-4×4C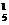 =170(个)。
=170(个)。
[例3]球台上有4个黄球,6个红球,击黄球入袋记2分,击红球入袋记1分,欲将此十球中的4球击入袋中,但总分不低于5分,击球方法有几种?
解:设击入黄球x个,红球y个符合要求,
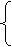 则有
x+y=4,
则有
x+y=4,
2x+y≥5(x、y∈N),得1≤x≤4.
∴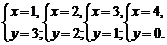
相应每组解(x,y),击球方法数分别为C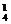 C
C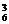 ,C
,C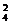 C
C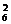 ,C
,C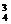 C
C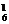 ,C
,C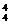 C
C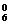 .
.
共有不同击球方法数为C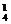 C
C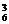 +C
+C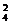 C
C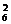 +C
+C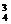 C
C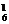 +C
+C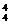 C
C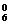 =195.
=195.
[例4]有11名外语翻译人员,其中5名英语翻译员,4名日语翻译员,另两名英、日语都精通,从中找出8人,使他们组成两个翻译小组,其中4人翻译英文,另4人翻译日文,这两个小组能同时工作,问这样的分配名单共可开出几张?
分析:既精通英语,又精通日语的“多面手”是特殊元素,所以可以从他们的参与情况入手进行分类讨论.
解:按“多面手”的参与情况分成三类.
第一类:多面手不参加,这时有C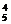 C
C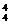 种;
种;
第二类:多面手中有一人入选,这时又有该人参加英文或日文翻译两种可能,因此有C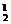 C
C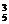 C
C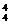 +C
+C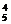 C
C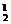 C
C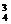 种;
种;
第三类:多面手中两个均入选,这时又分三种情况:两个都译英文、两个都译日文、两人各译一个语种,因此有C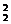 C
C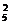 C
C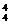 +C
+C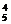 C
C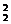 C
C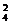 +C
+C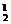 C
C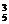 C
C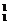 C
C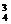 种.
种.
综上分析,共可开出C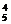 C
C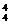 +C
+C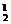 C
C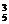 C
C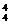 +C
+C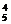 C
C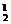 C
C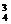 +C
+C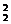 C
C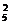 C
C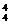 +C
+C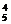 C
C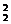 C
C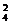 + C
+ C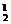 C
C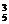 C
C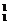 C
C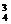 =
=
185种.
法2.先安排翻译英文人员,后安排翻译日文人员进行分类求解,共有
C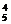 C
C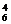 +C
+C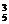 C
C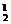 C
C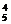 +C
+C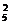 C
C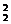 C
C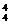 =185种.
=185种.
[研讨.欣赏]从1到100这100个正整数中,每次取出2个数使它们的和大于100,共有多少种取法?
解:(1)若取出的2个数都大于50,则有C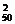 种.
种.
(2)若取出的2个数有一个小于或等于50,
当取1时,另1个只能取100,有C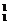 种取法;
种取法;
当取2时,另1个只能取100或99,有C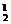 种取法;
种取法;
……
当取50时,另1个数只能取100,99,98,…,51中的一个,有C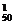 种取法,所以共有1+2+3+…+50=
种取法,所以共有1+2+3+…+50=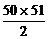 .
.
故取法种数为C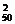 +
+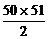 =
= +
+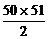 =2500.
=2500.
8.最短路径须走七步,只需确定哪三步向上,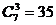 走法.类似得
走法.类似得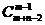 =
=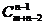 种走法。
种走法。
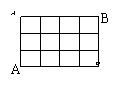
8. 从一个3×4的方格中的一个顶点A到对顶顶点B的
最短路线有________条;
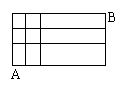 如果某城市由n条东西方向的街道和m条南北方向的街
如果某城市由n条东西方向的街道和m条南北方向的街
道组成一个矩形街道网,如图,要从A处走到B处,使所走
的路程最短,则不同的走法有_________种
◆练习简答:1-3.
BCD; 4.设素菜n种,则C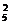 ·C
·C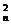 ≥200
≥200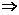 n(n-1)≥40,n的最小值为7; 5.1260; 6. C
n(n-1)≥40,n的最小值为7; 5.1260; 6. C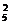 ·C
·C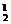 =20种; 7.让三只不亮的灯插空,C
=20种; 7.让三只不亮的灯插空,C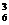 =20;
=20;
7. 马路上有编号为1,2,3,…,10的十只路灯,为节约用电又看清路面,可以把其中的三只灯关掉,但不能同时关掉相邻的两只或三只,在两端的灯也不能关掉的情况下,则满足条件的关灯方法有___________种.
马路上有编号为1,2,3,…,10的十只路灯,为节约用电又看清路面,可以把其中的三只灯关掉,但不能同时关掉相邻的两只或三只,在两端的灯也不能关掉的情况下,则满足条件的关灯方法有___________种.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com