
1.下列加点的字的读音,全都正确的一组是 ( )
A.发酵(xiào) 参与(yù) 内讧(gòng) 同仇敌忾(kài)
B.讣(bù)告 歼(qiān)灭 恪(kè)守 垂涎(xían)三尺
C.慰藉(jì) 谄(chǎn)媚 懦(nuò)弱 戛(gǎ)然而止
D.联袂(mèi) 创(chuàng) 伤 腼腆(tǐan) 莘莘(shēn)学子
12.已知集合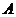 和集合
和集合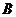 各含有12个元素,
各含有12个元素,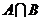 含有4个元素,求同时满足下面两个条件的集合
含有4个元素,求同时满足下面两个条件的集合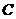 的个数:(1)
的个数:(1)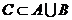 ,且
,且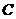 中含有3个元素;(2)
中含有3个元素;(2)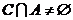 (
(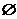 为空集).
为空集).
分析
该题是1986年的高考题,本题形式是集合,实质是计数问题,要用排列组合的方法求解.如图所示,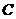 中的三个元素的取法不止一类,可考虑分类解之.
中的三个元素的取法不止一类,可考虑分类解之.
解
因为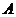 、
、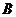 各有12个元素,
各有12个元素,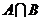 含有4个元素,所以
含有4个元素,所以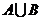 中元素的个数是
中元素的个数是 (个). 其中,属于
(个). 其中,属于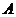 的元素有12个,属于
的元素有12个,属于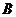 而不属于
而不属于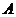 的元素有8个,要使
的元素有8个,要使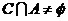 ,则组成
,则组成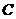 中的元素至少有一个含在
中的元素至少有一个含在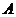 中,集合
中,集合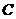 的个数是
的个数是
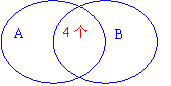 1)只含
1)只含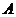 中1个元素的有
中1个元素的有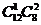 个.
个.
2)含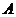 中2个元素的有
中2个元素的有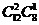 个;
个;
3)含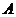 中3个元素的有
中3个元素的有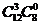 个.
个.
故所求的集合C的个数共有
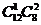 +
+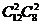 +
+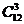 =1084(个).
=1084(个).
[探索题]某篮球队共7名老队员,5名新队员,根据下列情况分别求出有多少种不同的出场阵容.
(1)某老队员必须上场,某2新队员不能出场;
(2)有6名打前锋位,4名打后卫位,甲、乙两名既能打前锋又能打后卫位.
解:(1)C =126种.
=126种.
(2)以2名既擅长前锋位又能打后卫位的队员是否上场,且上场后是前锋还是后卫作分类标准:①甲、乙都不上场有C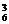 C
C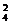 =120种;②甲、乙有一名上场,作前锋位有C
=120种;②甲、乙有一名上场,作前锋位有C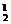 (C
(C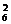 C
C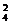 )种,作后卫位有C
)种,作后卫位有C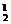 (C
(C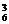 C
C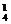 )种,共C
)种,共C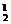 (C
(C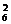 C
C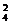 )+C
)+C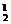 (C
(C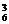 C
C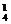 )=340种;③甲、乙都上场,有C
)=340种;③甲、乙都上场,有C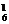 C
C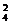 +C
+C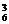 C
C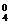 +C
+C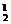 (C
(C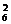 C
C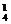 )=176种.据分类计数原理,共有120+340+176=636种.
)=176种.据分类计数原理,共有120+340+176=636种.
11.从1,2,…,30这前30个自然数中,每次取不同的三个数,使这三个数的和是3的倍数的取法有多少种?
解:令A={1,4,7,10,…,28},B={2,5,8,11,…29},C={3,6,9,…,30}组成四位数的方式有以下四类符合题意:①A,B,C中各取一个数,有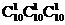 种;②仅在A中取3个数,有
种;②仅在A中取3个数,有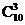 种;③仅在B中取3个数,有
种;③仅在B中取3个数,有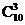 种;④仅在C中取3个数,有
种;④仅在C中取3个数,有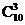 种,故由加法原理得:
种,故由加法原理得: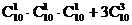 =1360种.
=1360种.
10. 已知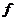 是集合
是集合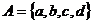 到集合
到集合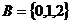 的映射
的映射
(1)不同的映射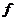 有多少个?
有多少个?
(2)若要求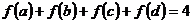 则不同的映射
则不同的映射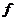 有多少个?
有多少个?
解:(1)A中每个元都可选0,1,2三者之一为像,由分步计数原理,共有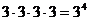 个不同映射
个不同映射
(2)根据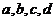 对应的像为2的个数来分类,可分为三类:
对应的像为2的个数来分类,可分为三类:
第一类:没有元素的像为2,其和又为4,必然其像均为1,这样的映射只有一个;
第二类:一个元素的像是2,其余三个元素的像必为0,1,1,这样的映射有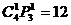 个;
个;
第三类:二个元素的像是2,另两个元素的像必为0,这样的映射有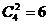 个
个
由分类计数原理共有1+12+6=19(个)
点评:问题(1)可套用投信模型:n封不同的信投入m个不同的信箱,有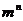 种方法;问题(2)的关键结合映射概念恰当确定分类标准,做到不重、不漏
种方法;问题(2)的关键结合映射概念恰当确定分类标准,做到不重、不漏
9.求值(1)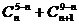 ; (2)已知
; (2)已知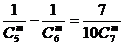 ,求
,求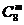
解:(1)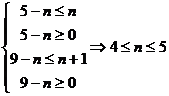 ,
,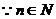 ,
,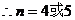
当n=4时,原式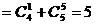 。
。
当n=5时,原式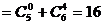 。
。
(2)本题运用公式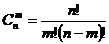 ,将已知等式转化为关于m的一元二次方程,解方程并结合m的取值范围确定m的值,最后计算
,将已知等式转化为关于m的一元二次方程,解方程并结合m的取值范围确定m的值,最后计算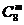
解:m的取值范围为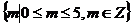
由已知,
即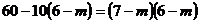
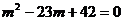 ,解得m=21或m=2
,解得m=21或m=2
但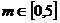 ,
, ,舍去
,舍去
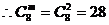
8.从一楼到两楼楼梯共10级,上楼可以一步上一级,也可以一步上两级,
 规定用8步走完楼梯的方法种数是
规定用8步走完楼梯的方法种数是
◆练习简答:1-4.ADAD; 1.先选一双有C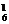 种,再从其余选2只,有C
种,再从其余选2只,有C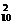 -C
-C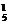 种,共C
种,共C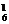 (C
(C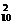 -C
-C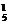 )=240种. 法2:
)=240种. 法2: 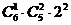 ; 2. C
; 2. C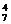 -C
-C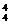 =34; 5.按含不含会双语的人分类,
=34; 5.按含不含会双语的人分类,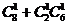 =20; 7. C
=20; 7. C -C
-C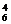 =195种. 法二:只能是4红,3红1白,2红2白,1红3白,有C
=195种. 法二:只能是4红,3红1白,2红2白,1红3白,有C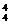 +C
+C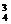 C
C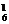 +C
+C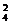 C
C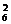 +C
+C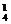 C
C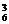 =195种. 8.有2步走2级,则
=195种. 8.有2步走2级,则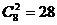 .
.
[解答题]
7.袋中有10个球,其中4个红球,6个白球,若取到1个红球记2分,取到1个白球记1分,那么从这10个球中取出4个,则总分不低于5分的取法有_______种
6.将一个四棱锥的每个顶点染上一种颜色,并使同一条棱的两端异色.若只有五种颜色可供使用,则不同的染色方法种数为_____________.
解析:设四棱锥为P-ABCD.(1)P:C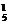 ,A:C
,A:C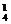 ,B:C
,B:C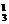 ,C与B同色:1,D:C
,C与B同色:1,D:C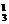 .
.
(2)P:C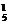 ,A:C
,A:C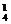 ,B:C
,B:C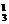 ,C与B不同色C
,C与B不同色C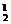 ,D:C
,D:C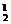 .
.
共有C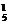 ·C
·C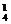 ·C
·C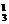 ·1·C
·1·C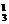 +C
+C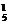 ·C
·C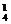 ·C
·C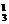 ·C
·C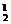 ·C
·C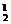 =420.
=420.
答案:420
5.某外语组有9人,每人至少会英语和日语中的一门,其中7人会英语,3人会日语,从中选取会英语和日语的各一人,则不同的选法有________种.
4.把一同排6张座位编号为1,2,3,4,5,6的电影票全部分给4个人,每人至少分1张,至多分2张,且这两张票具有连续的编号,那么不同的分法种数是( )
A.168 B.96 C.72 D.144
[填空题]
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com