
2.如果物体的运动轨迹不是直线,或不知道物体的运动是不是直线?应该建立怎样的坐标系?
1.在物理必修1的学习中,我们是如何定量描述物体的运动情况的?
(四)数字问题:注意0的特殊性,注意有无重复数字,注意数字位数
例如:用0,1,3,4,5六个数字组成无重复数字的数字,分别求下列各类数的个数
五位奇数,(2)能被5整除的三位数,(3)比20300大的五位数
(排列组合与二项式定理测试试卷16)
排列数组合数运算:
例如:排列组合与二项式定理测试试卷13
二项式定理:
排列组合与二项式定理测试试卷6、7、10、15
创新活页37页1、8、9、12
小结:
熟记二项式定理公式,会熟练应用公式得到二项展开式、二项展开式的第r+1项、常数项、含xi的项
熟记几个组合数公式性质以及推论,会熟练应用其求值f
会根据多项式还原二项式,注意项数以及次数的对应
会用赋值法求所有项系数的和
区别系数和二项式系数,并会求系数最大的项以及二项式系数最大的项
(三)分类选派问题:注意要分类清楚
分别选择问题,例如:4男5女中选择5人,要求至少2女,有多少种选法?
多面手问题,例如:8个人中有5人会英语,5人会日语,现在选日语和英语翻译各2人,有多少种选法?
(一)(1)相邻问题捆绑法,(2)不相邻问题插空法
(3)分排问题直排法,(4)定序问题除法
 (二)分组,分配问题
(二)分组,分配问题
平均分组(除)
部分平均分组(部分除) 若有分配任务就要排列
不平均分组
例如:(1)作业本上的
(2)排列组合与二项式定理测试试卷12、14(3)、17
1、 二项式定理
二项式定理
右边的多项式叫做(a+b)n的二项展开式,其中 Cnr an-rbr 叫做二项展开式的通项,记作Tr+1 ,Cnr 叫做 二项式系数.
2、二项展开式的特点:
(1)项数:共n+1项
(2)指数:a按降幂排列,b按升幂排列,每一项中a、b的指数和为n
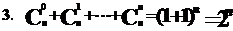 (3)系数:第r+1项的二项式系数为Cnr (r=0,1,2,…,n)
(3)系数:第r+1项的二项式系数为Cnr (r=0,1,2,…,n)
排列组合典型题解析:
三边长分别为整数,且最大边长为11的三角形的个数为______
在一块并排10垄的田地中选择2龙分别种植A、B两种作物,每种作物种一垄,要求两种作物之间间隔不得小于6垄,则不同的种植方法有_______种
将3种作物种植在如下图的5块试样田里,每块种植一种,且相邻的试验田不能种植同一种作物,则不同的种植方法有_______种
小结:按元素的性质进行分类,按事件发生的过程分步
正确使用两个基本计数原理的前提是要清楚俩个基本计数原理的使用条件,合理进行分类和分步。一定要做到分类明确,层次清楚,不重不漏;按逻辑分步。
5名成年人带两个小孩排队上山,小孩不排在一起也不排在头尾,共有____种排法
某天上午有 5节课,要排好语、数、外、体育、政治5门课,其中英语排在中间一节,体育不排在第1、2节,数学不排在最后一节,共有_____种排法
书架上原来有5本书,现将2本新书放入,不改变原有5本书位置,共有___种排法
8个人排两排,第一排3人,第二排5人,共有___种排法
10级台阶分3步走完,共有____种走法
小结:
1、解排列组合问题通常考察的是有附加条件的问题,解决这类问题通常有三种途径:
以元素为主,应先满足特殊元素的要求,再考虑其他元素
以位置为主,应先满足特殊位置的要求,再考虑其他位置
先不考虑附加条件,计算出总数再减去不符合条件的个数
求解排列组合问题常见题型方法
组合:一般地,从n个不同元素中取出m个不同元素并成一组,叫做从n个不同元素中取出m个不同元素的一个组合。
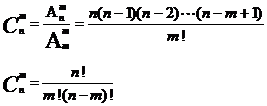 组合数公式:
组合数公式:
(组合数公式1-适用于计算)
(组合数公式2-适用于化简证明)
组合数公式性质:性质1: 
性质2: 
推论:1
推论2:
排列:一般地,从n个不同的元素中取出m(m﹤n)个元素,并按一定的顺序排成一列,叫做从n个不同元素中取出m个元素的一个排列。
注意:1、排列的定义中包含两个基本内容:①“取出元素”;②“按照一定顺序排列”,“一定顺序”就是与位置有关,这也是判断一个问题是不是排列问题的重要标志。
2、根据排列的定义,两个排列相同,是指当且仅当两个排列的元素完全相同,而且元素的排列顺序也相同
排列数公式: 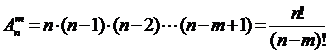
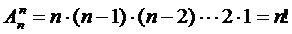
2、分步计数原理:完成一件事,需要分成n个步骤,做第一步有m1种不同的方法,做第二步有m2种不同的方法,……,做第n步有mn种不同的方法,那么完成这件事有
N=m1×m2×…×mn 种不同的方法。(乘法原理)
1、分类计数原理:完成一件事,有n类办法,在第一类办法中有m1种不同的方法,在第二类办法中有m2种不同的方法,……,在第n类办法中有mn种不同的方法,那么完成这件事共有 N=m1+m2+…+mn 种不同的方法。(加法原理)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com