2．如果两个不在同一直线上的分运动都是匀速直线运动，对其合运动的描述中，正确的是 (　　 )

　　 A．合运动一定是曲线运动

　　 B．合运动一定是直线运动　　

　　 C．合运动是曲线运动或直线运动

D．当两个分运动的速度数值相等时，合运动才为直线运动

1．一人游泳渡河以垂直河岸不变的速度(相对水)向对岸游去，河水流动速度恒定．下列说法中正确的是 ( 　　)

　　 A．河水流动速度对人渡河无任何影响

　　 B．游泳渡河的路线与河岸垂直

　　 C．由于河水流动的影响，人到达对岸的时间与静水中不同

D．由于河水流动的影响，人到达对岸的位置，向下游方向偏移

4．连带运动问题

指物拉绳(杆)或绳(杆)拉物问题。由于高中研究的绳都是不可伸长的，杆都是不可伸长和压缩的，即绳或杆的长度不会改变，所以解题原则是：把物体的实际速度分解为垂直于绳(杆)和平行于绳(杆)两个分量，根据沿绳(杆)方向的分速度大小相同求解。

例6　 如图所示，车甲以速度v₁拉车乙前进，乙的速度为v₂，甲、乙都在水平面上运动，求v₁∶v₂

解法1 　甲、乙沿绳的速度分别为v₁和v₂cosα，两者应该相等，所以有v₁∶v₂=cosα∶1

解法2　 　取OB=OC，Δt→0 　则∠CBA=90⁰　 AC=AB/cosα

v₁= v₂cosα

评析 　本题关键在于分清乙车运动速度v₂是合运动的速度，沿绳方向是分运动速度。

例7　 光滑的杆互相垂直地固定在一起，上面分别穿有一个小球，小球a、b间用一细直棒相连，如图。当细直棒与竖直杆夹角为α时，求两小球实际速度之比v_a∶v_b？

解析　 a、b沿杆的分速度分别为v_acosα和v_bsinα

∵v_acosα= v_bsinα　

∴v_a∶v_b= tanα∶1

[同步检测]

3．小船渡河问题

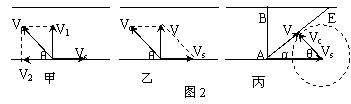
一条宽度为L的河，水流速度为V_s，已知船在静水中的航速为V_c，船过河时，船的实际运动(即相对于河岸的运动)可以看成是随水以速度V_s漂流的运动和以V_c相对于静水的划行运动的合运动。随水漂流和划行这两个分运动互不干扰而具有等时性。

(1)怎样渡河时间最短？

如图2-甲所示，设船头斜向上游与河岸成任意角θ，这时船速在垂直于河岸方向的速度分量V₁=V_csinθ,渡河所需时间为：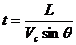

可以看出：L、V_c一定时，t随sinθ增大而减小；当θ=90⁰时，sinθ=1，所以，当船头与河岸垂直时，渡河时间最短，.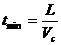

(2)若V_s＜V_c，怎样渡河位移最小？

如图2-乙所示，渡河的最小位移即河的宽度。为了使渡河位移等于L，必须使船的合速度V的方向与河岸垂直。这是船头应指向河的上游，并与河岸成一定的角度θ。根据三角函数关系有：V_ccosθ─V_s=0.

所以θ=arccos(V_s/V_c)，因为0≤cosθ≤1，所以只有在V_c>V_s时，船才有可能垂直于河岸横渡。

(3)若V_s＞V_c，怎样渡河位移最短？

如果水流速度大于船在静水中的航行速度，则不论船的航向如何，总是被水冲向下游。怎样才能使船的位移最短呢？如图2-丙所示，设船头V_c与河岸成θ角，合速度V与河岸成α角。可以看出：α角越大，船的位移越短，那么，在什么条件下α角最大呢？以V_s的矢尖为圆心，以V_c为半径画圆，当v与圆相切时，α角最大，根据cosθ=V_c/V_s，船头与河岸的夹角应为：θ=arccos(V_c/V_s)

此时渡河的最短位移为：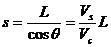

思考：过河的最短时间和最短位移分别决定于什么？

例5　 河宽d=100m ，水流速度为v₁=4m/s，船在静水中的速度是v₂=3m/s，求：

⑴ 欲使船渡河时间最短，船应怎样渡河？最短时间是多少？船经过的位移是多大？

⑵ 欲使船航行距离最短，船应怎样渡河？渡河时间多长？

解析： 设想水不流动，则船将以v₁速度做匀速直线运动，设想船不开行，则船将以v₂速度顺水飘流，可见实际渡河时，渡船同时参与两个分运动，其合运动沿v₁与 v₂矢量和的方向做匀速直线运动，由于分运动与合运动的等时性，船渡河时间等于v₁分运动的时间。

⑴ 不论v₁与v₂的大小如何，船头v₁的方向垂直指向河岸时，时间最短，

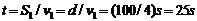
⑵ 因船速小于水速，故小船不能垂直过河，但有无最短航程呢？

虽然不能垂直过河，但有最短的路程，用画圆的方法可找出最短船程时夹角θ，并可找到这时速度之间关系满足的特征，如图。

则sinθ=v₁/v₂

S=d/sinθ　 ， t=s/v_合=d/(sinθ)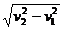

点评

⑴ 不论v₁与v₂的大小如何，当船头v₁的方向垂直指向河岸时，时间最短，且最短时间为 。

⑵ 当 时，合速度垂直过岸，航程最短为d　 ，当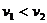 时不能垂直过岸，但仍有最短路程，此时船的实际航向与下游夹θ角，且sinθ=v₁/v₂ 。

2．决定合运动的性质和轨迹的因素

物体运动的性质由加速度决定(加速度为零时物体静止或做匀速运动；加速度恒定时物体做匀变速运动；加速度变化时物体做变加速运动)。

物体运动的轨迹(直线还是曲线)则由物体的速度和加速度的方向关系决定(速度与加速度方向在同一条直线上时物体做直线运动；速度和加速度方向成角度时物体做曲线运动)。

两个互成角度的直线运动的合运动是直线运动还是曲线运动？

决定于它们的合速度和合加速度方向是否共线(如图1所示)。　　

常见的类型有：

⑴ a=0：匀速直线运动或静止。

⑵ a恒定：性质为匀变速运动，分为：① v、a同向，匀加速直线运动；②v、a反向，匀减速直线运动；③ v、a成角度，匀变速曲线运动(轨迹在v、a之间，和速度v的方向相切，方向逐渐向a的方向接近，但不可能达到。)

⑶ a变化：性质为变加速运动，加速度大小、方向都随时间变化。

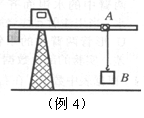
例4 　如图所示的塔吊臂上有一可以沿水平方向运动的小车A，小车下装有吊着物体B的吊钩，在小车A与物体B以相同的水平速度沿吊臂方向匀速运动的同时，吊钩将物体B向上吊起，A、B之间的距离以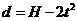 (SI)(SI表示国际单位制，式中H为吊臂离地面的高度)规律变化，则物体做(　　 )

A．速度大小不变的曲线运动．　

B．速度大小增加的曲线运动．

C．加速度大小方向均不变的曲线运动．

D．加速度大小方向均变化的曲线运动．

解析　 根据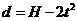可知，物体在竖直方向上做匀加速直线运动，水平方向为匀速直线运动，合加速度方向与合初速度的方向必不共线，物体做曲线运动，且加速度恒定为匀变速曲线运动，加速度方向与速度方向夹锐角，速度不断增大，所以答案为 B C。

1．关于运动的合成与分解

⑴ 合运动与分运动

定义：如果物体同时参与了几个运动，那么物体实际发生的运动就叫做那几个运动的合运动。那几个运动叫做这个实际运动的分运动．

特征：① 等时性：合运动所需时间和对应的每个分运动时间相等

② 独立性：一个物体可以同时参与几个不同的分运动，各个分运动独立进行，互不影响。

注意：在一个具体的问题中，判断哪个是合运动、哪个是分运动的依据是：物体的实际运动是哪个，那个实际运动就叫做合运动，即直接观察到的运动是合运动。

⑵ 运动的合成与分解

定义：从已知的分运动来求合运动，叫做运动的合成，求一个已知运动的分运动，叫运动的分解，运动的合成与分解包括位移、速度和加速度的合成，

意义：运动的合成与分解是解决复杂运动的一种基本方法，它的目的在于将复杂的运动化为简单的运动，将曲线运动化为直线运动，这样就可以应用已经掌握的简单运动或直线运动的规律来研究一些复杂的曲线运动，运动的合成或分解是认识和解决复杂运动问题的方法和手段。

方法：运动的合成和分解遵循平行四边形定则，如果各分运动都在同一直线上，我们可以选取沿该直线的某一方向作为正方向，与正方向相同的矢量取正值，与正方向相反的矢量取负值，这时就可以把矢量运算简化为代数运算。如果各分运动互成角度，那就要作平行四边形，运用作图法、解直角三角形等方法求解。

例1 　关于运动的合成与分解，以下说法正确的是(　　　 )

A．由两个分运动求合运动，合运动是唯一确定的

B．由合运动分解为两个分运动，可以有不同的分解方法

C．物体做曲线运动时，才能将这个运动分解为两个分运动

D．任何形式的运动，都可以用几个分运动代替

解析　 从运动合成或分解的法则--平行四边形法则出发思考，明确运动分解的意义、方法，可做出正确的判断，答案为ABD

例2 　在一无风的雨天，雨滴竖直下落至地表的速度v₁=8 m/s，一辆汽车以v₂=6 m/s的速度匀速行驶，求车上的人看到雨滴的速度大小与方向。

解析　 如图所示，当观察者处于汽车上时，观察到雨滴同时参与两个分运动，一是竖直下落运动，二是朝向汽车的运动，此运动的速度v₂′与v₂大小相等、方向相反，所以雨滴相对汽车的速度v为v₁、v₂′的合速度

v=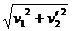=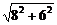m/s=10 m/s

设v与竖直方向的夹角为α

则tanα=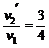　　 所以α≈37°

速度方向与竖直方向夹角为37°偏向后

例3 　玻璃板生产线上，宽9m的成型玻璃板以4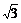m/s的速度连续不断地向前行进，在切割工序处，金刚钻的走刀速度为8m/s，为了使割下的玻璃板都成规定尺寸的矩形，金刚钻割刀的轨道应如何控制？切割一次的时间多长？

解析　 要切成矩形则割刀相对玻璃板的速度垂直v，如图设v_刀与v_玻方向夹角为θ，cosθ=v_玻/v_刀=4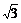/8，则θ=30⁰。v=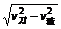==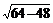4m/s ，时间为t=s/v=9/4=2.25s

6．曲线运动的轨迹夹在___________和____________之间且总是朝着_____________方向弯曲。

[同步导学]

5．初速度为v₀，加速度为a的匀加速直线运动可看作哪两个分运动的合运动？从该角度推导其速度公式和位移公式。

4．运动的合成和分解，是指________________的合成与分解，必须遵循______________。

3．_____________叫做运动的合成，_____________叫做运动的分解。