18．(12分)(2009·全国卷Ⅰ)设函数f(x)＝x³+3bx²+3cx有两个极值点x₁、x₂，且x₁∈[－1,0]，x₂∈[1,2]．

(1)求b、c满足的约束条件，并在下面的坐标平面内，画出满足这些条件的点(b，c)的区域；

图1

(2)证明：－10≤f(x₂)≤－.

解：(1)f′(x)＝3x²+6bx+3c，依题意知，方程f′(x)＝0有两个根x₁、x₂，且x₁∈[－1,0]，x₂∈[1,2]等价于f′(－1)≥0，f′(0)≤0，f′(1)≤0，f′(2)≥0.

由此得b、c满足的约束条件为

满足这些条件的点(b，c)所构成的区域为图中阴影部分．

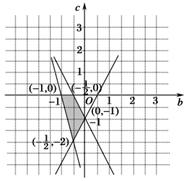
图2

(2)由题设知f′(x₂)＝3x+6bx₂+3c＝0，故bx₂＝－x－c，于是f(x₂)＝x+3bx+3cx₂＝－x+x₂.

由于x₂∈[1,2]，而由(1)知c≤0，

故－4+3c≤f(x₂)≤－+c.

又由(1)知－2≤c≤0，所以－10≤f(x₂)≤－.

17．(12分)(2010·湖北八校联考)已知函数f(x)＝ax²+2x+1(a∈R)．

(1)若f(x)的图象与x轴恰有一个公共点，求a的值；

(2)若方程f(x)＝0至少有一正根，求a的范围．

解：(1)若a＝0，则f(x)＝2x+1，f(x)的图象与x轴的交点为(－，0)，满足题意．

若a≠0，则依题意得：Δ＝4－4a＝0，即a＝1.故a＝0或1.

(2)显然a≠0.

若a<0，则由x₁x₂＝<0可知，方程f(x)＝0有一正一负两根，此时满足题意．

若a>0，则Δ＝0时，x＝－1，不满足题意；Δ>0时，方程有两负根，也不满足题意．故a<0.

16．给出下列四个命题：①函数f(x)＝x|x|+bx+c为奇函数的充要条件是c＝0；②函数y＝2^－x的反函数是y＝－log₂x

(x>0)；③若函数f(x)＝lg(x²+ax－a)的值域是R，则a≤－4或a≥0；④若函数y＝f(x－1)是偶函数，则函数y＝f(x)的图象关于直线x＝1对称．其中所有正确命题的序号是__________．

解析：依题意，因为f(x)＝x|x|+bx+c为奇函数，所以f(－x)＝－x|x|－bx+c＝－f(x)＝－x|x|－bx－c，所以c＝0，①正确；由y＝2^－x解得x＝－log₂y，即函数y＝2^－x的反函数为y＝－log₂x，②正确；函数f(x)＝lg(x²+ax－a)的值域为R，则Δ＝a²+4a≥0，解得a≤－4或a≥0，所以③正确；因为函数y＝f(x－1)是偶函数，则图象关于y轴对称，y＝f(x)的图象由函数y＝f(x－1)的图象向左平移一个单位得到，则y＝f(x)的图象关于直线x＝－1对称，所以④错．

答案：①②③

15．(2009·福州质检)对于函数f(x)定义域中任意的x₁，x₂(x₁≠x₂)，有如下结论：

①f(x₁+x₂)＝f(x₁)f(x₂)；

②f(x₁·x₂)＝f(x₁)+f(x₂)；

③>0；

④f()<.

当f(x)＝2^x时，上述结论中正确结论的序号是__________．

解析：代特殊值验证即可．

答案：①③④

14．已知函数g(x)在(0，+∞)上是增函数，g(x)＝f(|x|)．若f(x)＝lgx，则g(lgx)>g(1)时x的取值范围是________．

解析：根据题意知g(x)＝lg|x|，又因为g(lgx)>g(1)，所以|lgx|>1，解得0<x<或x>10.

答案：(0，)∪(10，+∞)

13．已知函数f(x)＝则f＝________.

解析：f＝log₃＝－2，f＝f(－2)＝2^－2＝.

答案：

12．(2010·东城一模)已知函数f(x)＝x²+bx的图象在点A(1，f(1))处的切线斜率为3，数列{}的前n项和为S_n，则S₂₀₀₉的值为　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A.　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 B.

C.　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 D.

解析：∵函数f(x)＝x²+bx的图象的切线的斜率为f′(x)＝2x+b；∴函数f(x)＝x²+bx的图象在点A(1，f(1))处的切线l的斜率为k＝2+b；∴2+b＝3，即b＝1；∴f(x)＝x²+x⇒＝＝＝－；

∴S₂₀₀₉＝(1－)+(－)+(－)+…+(－)＝1－＝.

答案：C

11．(2010·湖北五校联考)已知f(x)是定义在R上的且以2为周期的偶函数，当0≤x≤1时，f(x)＝x²，如果直线y＝x+a与曲线y＝f(x)恰有两个交点，则实数a的值是　　　 (　)

A．0　 　　　　　　　　　　　　　　　　　　　　　　　　　　　 B．2k(k∈Z)

C．2k或2k－(k∈Z)　 　　　　　　　　　　　　　　 D．2k或2k+(k∈Z)

解析：令a＝0，a＝－均符合题意，故选C.

答案：C

10．(2009·福建质检)函数y＝的图象大致是　　　　　　　　　　　　　　　　　　　　　　　 (　)

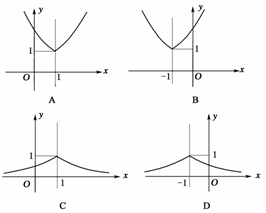
解析：令x＝0，得y＝；令x＝1，得y＝1，

∴图象过(0，)，(1,1)两点，故选C.

答案：C

9．(2010·河南重点中学联考)已知函数f(x)是定义在(－2,2)上的奇函数，当x∈(0,2)时，f(x)＝2^x－1，则f(log₂)的值为　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A．－2　 　　　　　　　　　　　　　　　　　　　　　　　　 B．－

C．2　 　　　　　　　　　　　　　　　　　　　　　　　　　　 D.－1

解析：当x∈(－2,0)时，－x∈(0,2)，又∵当x∈(0,2)时，f(x)＝2^x－1，∴f(－x)＝2^－x－1，又因函数f(x)是定义在(－2,2)上的奇函数，∴f(－x)＝－f(x)＝2^－x－1，

∴x∈(－2,0)时，f(x)＝1－.∵－2<log₂<0，

∴f(log₂)＝1－＝－2.故选A.

答案：A