
13.(本小题满分14分)
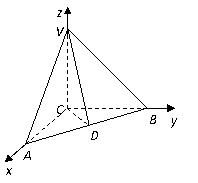
如图,三棱柱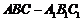 中,侧面
中,侧面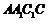
 底面
底面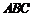 ,
,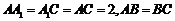 ,
,
且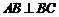 ,O为
,O为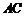 中点.
中点.
(Ⅰ)证明: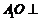 平面
平面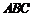 ;
;
(Ⅱ)求直线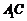 与平面
与平面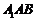 所成角的正弦值;
所成角的正弦值;
 (Ⅲ)在
(Ⅲ)在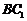 上是否存在一点
上是否存在一点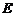 ,使得
,使得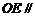 平面
平面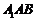 ,若不存在,说明理由;若存在,确定点
,若不存在,说明理由;若存在,确定点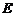 的位置.
的位置.
2.(本小题满分12分)
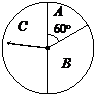
某商场为吸引顾客消费推出一项优惠活动.活动规则如下:消费额每满100元可转动如图所示的转盘一次,并获得相应金额的返券,假定指针等可能地停在任一位置. 若指针停在A区域返券60元;停在B区域返券30元;停在C区域不返券. 例如:消费218元,可转动转盘2次,所获得的返券金额是两次金额之和.
(Ⅰ)若某位顾客消费128元,求返券金额不低于30元的概率;
(Ⅱ)若某位顾客恰好消费280元,并按规则参与了活动,他获得返券的金额记为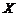 (元).求随机变量
(元).求随机变量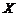 的分布列和数学期望.
的分布列和数学期望.
1.(本小题满分12分)
已知函数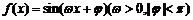 的图象如图所示.
的图象如图所示.
(Ⅰ)求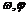 的值;
的值;
(Ⅱ)设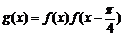 ,求函数
,求函数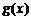 的单调递增区间.
的单调递增区间.

22.(本题满分12分)
解:(1)设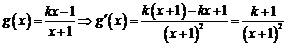 , ………………3分
, ………………3分
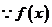 是
是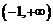 上的增函数,且
上的增函数,且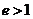 ,
,
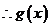 是
是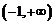 上的增函数,
上的增函数,
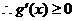 ,得到
,得到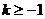 ;
;
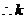 的取值范围为
的取值范围为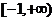 …………………5分
…………………5分
(2)由条件得到 ,
,
猜想最大整数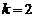 ………………………6分
………………………6分
现在证明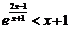 对任意
对任意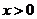 恒成立,
恒成立,
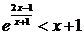 等价于
等价于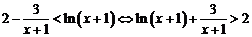 , ………….8分
, ………….8分
设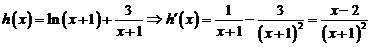 ,…………….9分
,…………….9分
当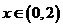 时,
时,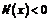 ,当
,当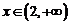 时,
时,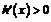 ,
…………………10分
,
…………………10分
所以对任意的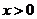 都有
都有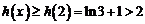 , ………………….11分
, ………………….11分
即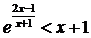 对任意
对任意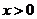 恒成立;
恒成立;
所以整数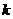 的最大值为2.
…………………………….12分
的最大值为2.
…………………………….12分
6.(本题满分14分)
解:(1)由|PF1|-|PF2|=2<|F1F2|知,点P的轨迹S是以F1、F2为焦点的双曲线右支.
由c=2,2a=2,∴b2=3.故轨迹S的方程为x2-=1 (x≥1) …….……4分
(2)当直线l的斜率存在时,设直线方程为y=k(x-2),P(x1,y1),Q(x2,y2),与双曲线方程联立消y得
(k2-3)x2-4k2x+4k2+3=0. …………5分
 ∴
∴ 解得k2>3.……
7分
解得k2>3.……
7分
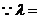 |AP|·|BQ|=
|AP|·|BQ|=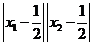 =(2x1-1)(2x2-1)
=(2x1-1)(2x2-1)
=[4x1x2-2(x1+x2)+1]=x1x2-+
=-+=+=+>. ………..…………..9分
当斜率不存在时,|AP|·|BQ|=,∴λ的最小值为. ………………10分
此时,|PQ|=6,|MF2|=3,S△PMQ=|MQ|·|PQ|=9. ………………12分
5.(本题满分14分)
解:(1)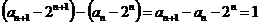 (与
(与 无关)
.…………4分
无关)
.…………4分
故数列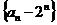 为等差数列,且公差
为等差数列,且公差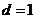 .
……………………5分
.
……………………5分
(2)由(1)可知,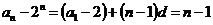 ,故
,故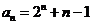 ………6分
………6分
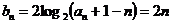 ……………………7分
……………………7分
方法一:数学归纳法
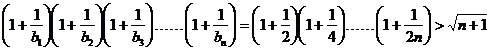
(1)当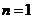 时,
时,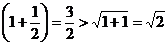 ,不等式成立,
…………8分
,不等式成立,
…………8分
(2)假设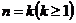 时不等式成立,
时不等式成立,
即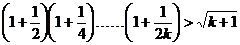 , ………………………….9分
, ………………………….9分
那么当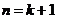 时,
时,
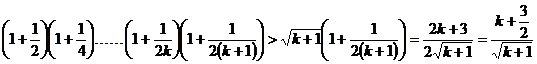
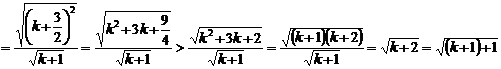
这说明,当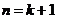 时不等式也成立 …………………………………11分
时不等式也成立 …………………………………11分
综上可知,对于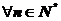 ,原不等式均成立. ……………………………12分
,原不等式均成立. ……………………………12分
方法二:均值不等式

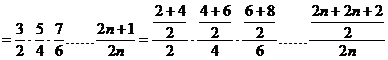 ……………9分
……………9分
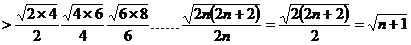 .
.
原不等式得证. ……………………12分
3.(本题满分14分)
解:记第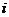 名用户选择的应用属于农场、音乐、读书分别为事件
名用户选择的应用属于农场、音乐、读书分别为事件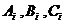 ,i=1,2,3.由题意知
,i=1,2,3.由题意知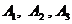 相互独立,
相互独立,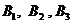 相互独立,
相互独立,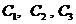 相互独立,
相互独立,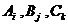 (i,j,k=1,2,3且i,j,k互不相同)相互独立,且
(i,j,k=1,2,3且i,j,k互不相同)相互独立,且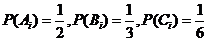 .
.
(1)他们选择的应用互不相同的概率
|

(2)设3位用户选择的应用是QQ读书的人数是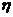 ,由已知
,由已知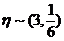 ,且
,且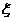 =3-
=3-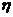 ,
,
所以
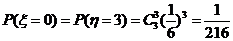
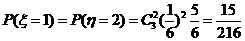
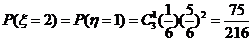
|
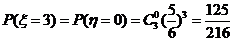
(每求对一个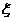 的概率给1分)
的概率给1分)
故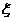 的分布列是
的分布列是
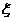
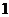
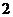
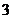
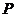
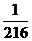
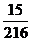
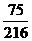
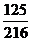
……………………10分
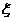 的数学期望是
的数学期望是
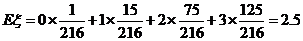
(或者由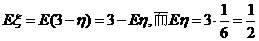 ,
,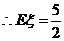 ) ……….12分
) ……….12分
2.(本题满分12分)
解法1:(1)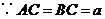
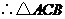 是等腰三角形,
是等腰三角形,

又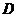 是
是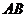 的中点
的中点
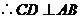 ,
………..…………1分
,
………..…………1分
又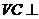 底面
底面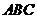
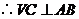 ………………2分
………………2分
于是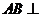 平面
平面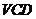 .
………………3分
.
………………3分
又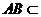 平面
平面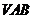
 平面
平面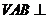 平面
平面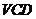 . …………4分
. …………4分
(2)过点 在平面
在平面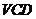 内作
内作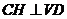 于
于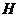 ,连接
,连接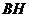 ………………5分
………………5分
则由(1)知AB⊥CH, ∴CH⊥平面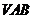 ………………6分
………………6分
于是 就是直线
就是直线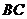 与平面
与平面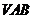 所成的角
………………7分
所成的角
………………7分
在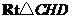 中,CD=
中,CD=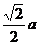 ,
, 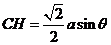 ; ………………8分
; ………………8分
设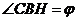 ,在
,在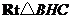 中,
中,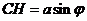 ………………9分
………………9分
 ………………10分
………………10分
 ,
,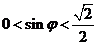 ……11分
……11分
又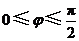 ,
,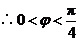
即直线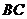 与平面
与平面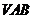 所成角的取值范围为
所成角的取值范围为
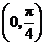 .
………………12分
.
………………12分
解法2:
(1)以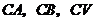 所在的直线分别为
所在的直线分别为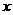 轴、
轴、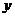 轴、
轴、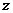 轴,建立如图所示的空间直角坐标系,则
轴,建立如图所示的空间直角坐标系,则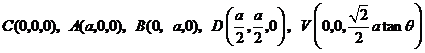 ,…1分
,…1分
于是,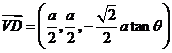 ,
,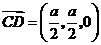 ,
,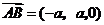 .
.
从而 ,即
,即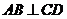 .…2分
.…2分
 同理
同理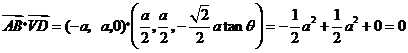 ,…3分
,…3分
即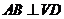 .又
.又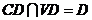 ,
,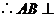 平面
平面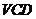 .
.
又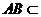 平面
平面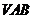 .
.
 平面
平面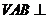 平面
平面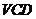 .
………………4分
.
………………4分

(2)设直线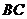 与平面
与平面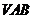 所成的角为
所成的角为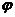 ,平面
,平面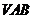 的一个
的一个
法向量为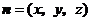 ,则由
,则由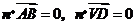 .
.
得 ………………6分
………………6分
可取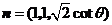 ,又
,又 ,
,
于是 ,
………………10分
,
………………10分
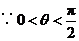 ,
,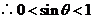 ,
,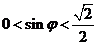 .又
.又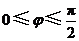 ,
,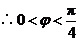 .
.
即直线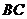 与平面
与平面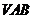 所成角的取值范围为
所成角的取值范围为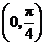 .
………………12分
.
………………12分
1.(本题满分12分)
解:(1)∵
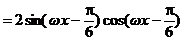
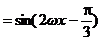 .
.................................3分
.
.................................3分
而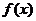 的最小正周期为
的最小正周期为 ,且
,且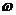 >0,∴
>0,∴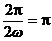 ,∴
,∴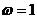 . ...............5分
. ...............5分
(2)由(1)得 .
.
若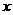 是三角形的内角,则
是三角形的内角,则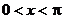 ,∴
,∴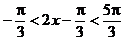 .
.
令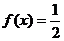 ,得
,得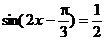 ,
,
∴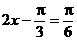 或
或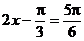 , ∴
, ∴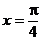 或
或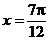 .
…………7分
.
…………7分
由已知,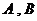 是△
是△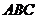 的内角,
的内角,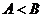 且
且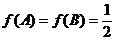 ,
,
∴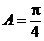 ,
,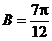 , ∴
, ∴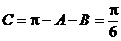 . ….…………………8分
. ….…………………8分
又由正弦定理,得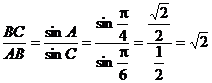 . …..…………10分
. …..…………10分
6.(本小题满分12分)
已知函数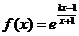 (e是自然对数的底数).
(e是自然对数的底数).
(1)若函数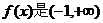 上的增函数,求k的取值范围;
上的增函数,求k的取值范围;
(2)若对任意的 ,求满足条件的最大整数k的值.
,求满足条件的最大整数k的值.
华侨中学2010届高三解答题限时训练1答案
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com