

5. 解:(Ⅰ)因为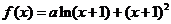 ,
,
所以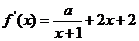 .
……2分
.
……2分
由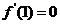 ,可得
,可得  ,
,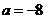 .
.
经检验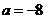 时,函数
时,函数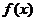 在
在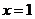 处取得极值,
处取得极值,
所以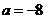 .
………4分
.
………4分
(Ⅱ)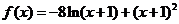 ,数学驿站
,数学驿站
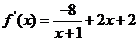
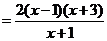 .
……6分
.
……6分
而函数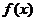 的定义域为
的定义域为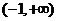 ,
,
当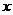 变化时,
变化时,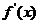 ,
,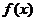 的变化情况如下表:
的变化情况如下表:
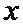 |
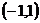 |
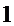 |
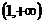 |
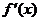 |
- |
0 |
+ |
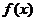 |
↘ |
极小值 |
↗ |
由表可知,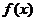 的单调减区间为
的单调减区间为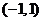 ,
,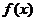 的单调减区间为
的单调减区间为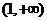 .……9分
.……9分
(3)∵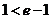 ,
,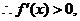
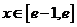 时,
时,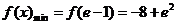 …10分
…10分
不等式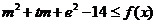 对任意
对任意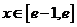 及
及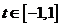 恒成立,即
恒成立,即
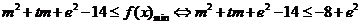 ,
,
即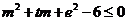 对
对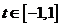 恒成立,
…12分
恒成立,
…12分
令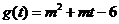 ,
,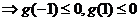
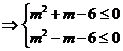 ,
,
解得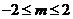 为所求.
…14分
为所求.
…14分
4.(1)解据已知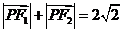 ,所求曲线
,所求曲线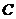 是椭圆,长轴
是椭圆,长轴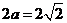 ,
,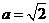 ,
,
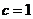 ,所以椭圆的方程为
,所以椭圆的方程为 .
……4分
.
……4分
(2)设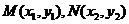 ,由
,由 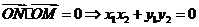 ,设
,设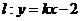 ,
,
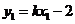 ,
,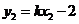 ,
,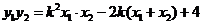 ,
,
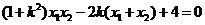
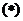 .联立
.联立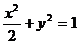 ,得
,得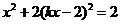 ,
,
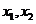 为上述方程的两根,
为上述方程的两根,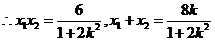 代入
代入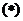 得
得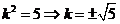 ,所求直线
,所求直线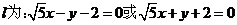 ------9分
------9分
(3)椭圆的右准线为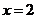 ,设点
,设点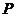 到右准线的距离为
到右准线的距离为 ,则
,则 ,
,
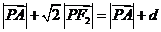 ,此时
,此时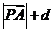 的最小值为点
的最小值为点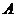 到右准线
到右准线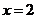 的距离,
的距离,
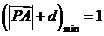 ,此时点
,此时点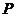 的坐标为
的坐标为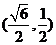 .
------14分
.
------14分
3.(1)证明:由已知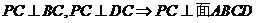 ……2分
……2分
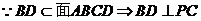 ,数学驿站
,数学驿站
又因为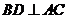 ,
, 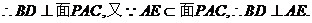 ……4分
……4分
(2)解法一:连AC交BD于点O,连PO,由(1)知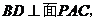

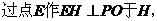 则
则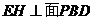 ,
,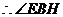 为
为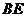 与平面
与平面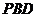 所成的角. 8分
所成的角. 8分
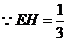 ,
,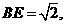 则
则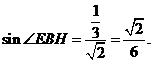 …10分
…10分
法二:空间直角坐标法,略.
(3)解:以正方形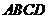 为底面,
为底面,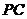 为高补成长方体,此时对角线
为高补成长方体,此时对角线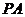 的长为球的直径,
的长为球的直径,
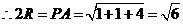 ,
,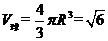 . …14分
. …14分
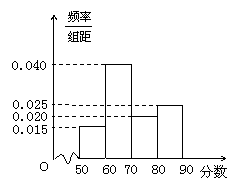
2.解:(1)因为0.015×10=0.15,0.04×10=0.4,在频率分布直方图中,中位数左边和右边的面积相等,所以中位数在区间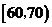 内
……3分
内
……3分
设中位数为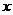 ,则
,则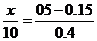 ,解得
,解得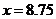 ……4分
……4分
估计该系统所属企业评估得分的中位数是68.75. ……5分
(2)据题意,整改后优秀企业的频率为10×0.025=0.25,不合格企业,良好企业的频率
成等差数列. ……6分
设该等差数列的首项为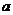 ,公差为
,公差为 ,
,
则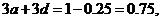 即
即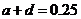 ,
……8分
,
……8分
设该系统所属企业获得贷款的均值为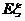 ,则
,则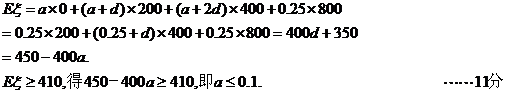
故整改后不合格企业占企业总数的百分比的最大值是10% ……12分
1.解:(Ⅰ)由图象知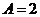
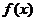 的最小正周期
的最小正周期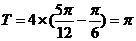 ,故
,故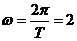 3分
3分
将点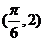 代入
代入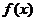 的解析式得
的解析式得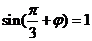 ,又
,又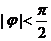 , ∴
, ∴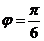
故函数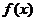 的解析式为
的解析式为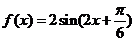 …6分
…6分
(Ⅱ)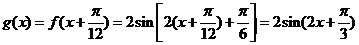 ……8分
……8分
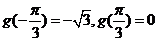 ,
,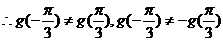 ……10分
……10分
 ,
,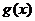 为非奇非偶函数.
……12分
为非奇非偶函数.
……12分
6.(本题满分14分)
已知数列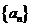 的首项为
的首项为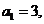 点
点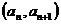 在直线
在直线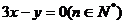 上.
上.
(Ⅰ)求数列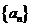 的通项公式;
的通项公式;
(Ⅱ)若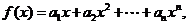 求
求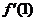 的值,并化简.
的值,并化简.
(Ⅲ)若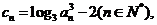 证明对任意的
证明对任意的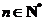 ,不等式
,不等式
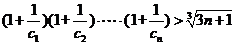 恒成立.
恒成立.
华侨中学2010届高三解答题限时训练1答案
5. (本题满分14分)已知函数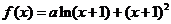 在
在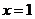 处有极值.
处有极值.
(Ⅰ)求实数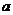 值;数学驿站
值;数学驿站
(Ⅱ)求函数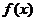 的单调区间;
的单调区间;
(Ⅲ)试问是否存在实数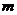 ,使得不等式
,使得不等式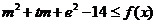 对任意
对任意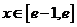 及
及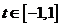 恒成立?若存在,求出
恒成立?若存在,求出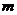 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.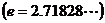
4. (本题满分14分)已知动点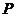 的轨迹为曲线
的轨迹为曲线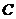 ,且动点
,且动点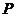 到两个定点
到两个定点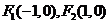 的距离
的距离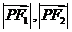 的等差中项为
的等差中项为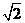 .
.
(Ⅰ)求曲线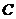 的方程;
的方程;
(Ⅱ)直线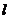 过圆
过圆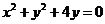 的圆心
的圆心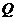 与曲线
与曲线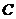 交于
交于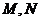 两点,且
两点,且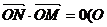 为坐标原点),求直线
为坐标原点),求直线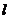 的方程;
的方程;
(Ⅲ)设点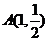 ,点
,点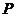 为曲线
为曲线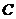 上任意一点,求
上任意一点,求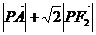 的最小值,并求取得最小值时点
的最小值,并求取得最小值时点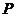 的坐标.
的坐标.
3.(本题满分14分)
已知四棱锥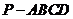 的三视图如下图所示,其中主视图、侧视图是直角三角形,俯视图是有一条对角线的正方形.
的三视图如下图所示,其中主视图、侧视图是直角三角形,俯视图是有一条对角线的正方形. 是侧棱
是侧棱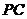 上的动点.
上的动点.
(Ⅰ)求证: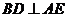
(Ⅱ) 若
若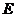 为
为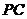 的中点,求直线
的中点,求直线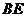 与平面
与平面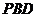 所成角的正弦值;
所成角的正弦值;
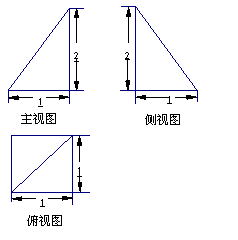
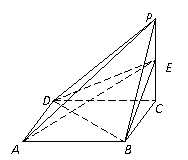 (Ⅲ)若五点
(Ⅲ)若五点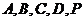 在同一球面上,求该球的体积.
在同一球面上,求该球的体积.
2.(本题满分12分)
2008年金融风暴横扫全球。为抗击金融风暴,市工贸系统决定对所属企业给予低息贷款的扶持.该系统先根据相关评分标准对各个企业进行了评估,并依据评估得分将这些企业分别评定为优秀、良好、合格、不合格4个等级,然后根据评估等级分配相应的低息贷款金额,其评估标准和贷款金额如下表:
为了更好地掌控贷款总额,该系统随机抽查了所属部分企业的评估分数,得其频率分布直方图如下:
(Ⅰ)估计该系统所属企业评估得分的中位数;
 (Ⅱ)该系统要求各企业对照评分标准进行整改,若整改后优秀企业数量不变,不合格企业、合格企业、良好企业的数量依次成等差数列,系统所属企业获得贷款的均值(即数学期望)不低于410万元,那么整改后不合格企业占企业总数的百分比的最大值是多少?
(Ⅱ)该系统要求各企业对照评分标准进行整改,若整改后优秀企业数量不变,不合格企业、合格企业、良好企业的数量依次成等差数列,系统所属企业获得贷款的均值(即数学期望)不低于410万元,那么整改后不合格企业占企业总数的百分比的最大值是多少?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com