
6.(本小题满分12分)
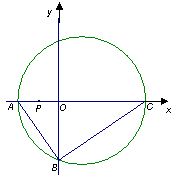
如图,直角三角形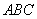 的顶点坐标
的顶点坐标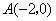 ,直角顶点
,直角顶点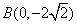 ,顶点
,顶点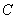 在
在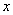 轴上,点
轴上,点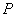 为线段
为线段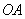 的中点
的中点
 (Ⅰ)求
(Ⅰ)求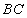 边所在直线方程;
边所在直线方程;
(Ⅱ)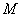 为直角三角形
为直角三角形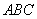 外接圆的圆心,求圆
外接圆的圆心,求圆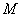 的方程;
的方程;
(Ⅲ)若动圆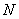 过点
过点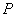 且与圆
且与圆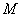 内切,求动圆
内切,求动圆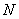 的圆心
的圆心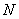 的轨迹方程.
的轨迹方程.
华侨中学2010届高三解答题限时训练3答案
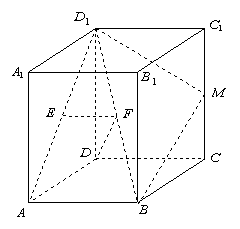
5.如图,已知长方体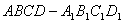 底面
底面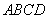 为正方形,
为正方形,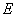 为线段
为线段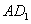 的中点,
的中点,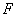 为线段
为线段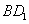 的中点.
的中点.
(Ⅰ)求证: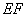 ∥平面
∥平面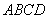 ;
;
(Ⅱ)设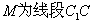 的中点,当
的中点,当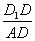 的比值为多少时,
的比值为多少时, 并说明理由.
并说明理由.
4.
4(本小题满分14分)已知函数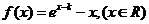
(1)当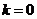 时,若函数
时,若函数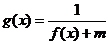 的定义域是R,求实数
的定义域是R,求实数 的取值范围;
的取值范围;
(2)试判断当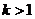 时,函数
时,函数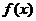 在
在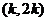 内是否存在零点.
内是否存在零点.
3.
33 (本小题满分14分) 设向量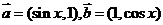 ,
,
记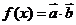 ,
,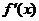 是
是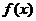 的导函数.
的导函数.
(I)求函数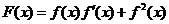 的最大值和最小正周期;
的最大值和最小正周期;
(II)若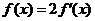 ,求
,求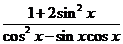 的值.
的值.
2.(本小题满分12分)在等差数列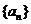 中,设
中,设
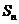 为它的前
为它的前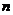 项和,若
项和,若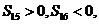 且点
且点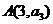 与
与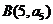 都在斜率为-2的直线
都在斜率为-2的直线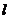 上,
上,
(Ⅰ)求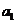 的取值范围;
的取值范围;
(Ⅱ)指出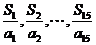 中哪个值最大,并说明理由.
中哪个值最大,并说明理由.
1.(本小题满分12分)
已知全集
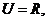 集合
集合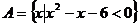 ,
,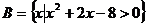 ,
, ,若
,若 ,求实数
,求实数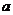 的取值范围.
的取值范围.
21.
解(1)证: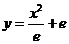
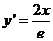 由
由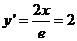 得
得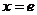 …………2分
…………2分
在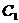 上点
上点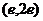 处的切线为
处的切线为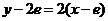 ,即
,即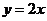 …………3分
…………3分
又在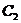 上点
上点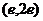 处切线可计算得
处切线可计算得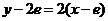 ,即
,即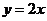
∴直线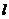 与
与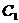 、
、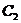 都相切,且切于同一点(
都相切,且切于同一点( )
…………………4分
)
…………………4分
(2)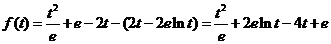
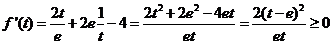 …………………6分
…………………6分
∴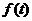 在
在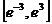 上递增
上递增
∴当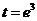 时
时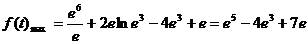 ……………8分
……………8分
(3)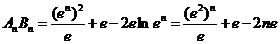
设上式为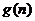 ,假设
,假设 取正实数,则
取正实数,则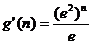 ·
·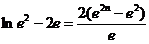
当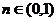 时,
时,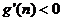 ,
,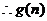 递减;
递减;
当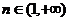 ,
,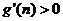 ,
,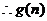 递增. ……………………………………12分
递增. ……………………………………12分
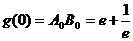
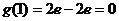
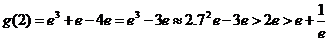
∴不存在正整数 ,使得
,使得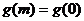
即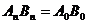 …………………………………………14分
…………………………………………14分
12分
6.(本题满分14分)
5.解证:(I)易得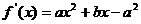 …………………………………………1分
…………………………………………1分
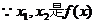 的两个极值点
的两个极值点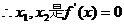 的两个实根,又a>0
的两个实根,又a>0
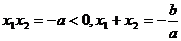 ……………………………………………………3分
……………………………………………………3分
∴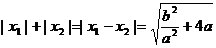 ∵
∵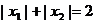
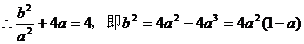
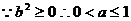 ……7分
……7分
(Ⅱ)设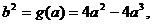 则
则
由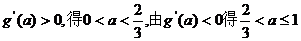
 上单调递增………………10分
上单调递增………………10分
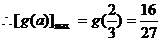
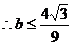 ………………………………………………12分
………………………………………………12分
4.解证:(Ⅰ)由题意知Sn=2an-3n
∴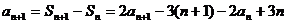
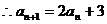 ………………2分
………………2分
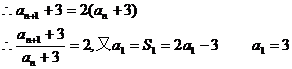 ∴a1+3=6……………4分
∴a1+3=6……………4分
∴数列{an+3}成以6为首项以2为公比的等比数列
(Ⅱ)由(I)得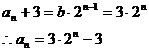 (Ⅲ)设存在s、p、r∈N*且s<p<r使as,ap,ar成等差数列∴2ap=as+ar∴
(Ⅲ)设存在s、p、r∈N*且s<p<r使as,ap,ar成等差数列∴2ap=as+ar∴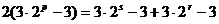
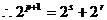 ………………9分
………………9分
即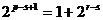 (*)∵s、p、r∈N*且s<p<r
(*)∵s、p、r∈N*且s<p<r
∴ 为奇数∴(*)为矛盾等式,不成立故这样的三项不存在。…12分
为奇数∴(*)为矛盾等式,不成立故这样的三项不存在。…12分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com