
5.解:
(1)由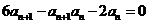
得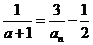 ,
,
则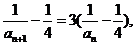
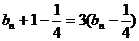
所以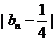 是以3为公比,
是以3为公比,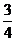 为首项的等比数列
为首项的等比数列
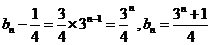 4分
4分
(2)当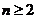 时,
时,
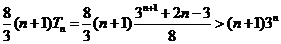
令
则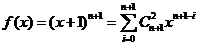
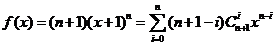
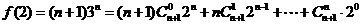
所以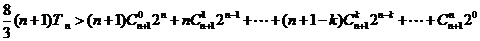
……13分
4.解:
设B型号电视机的价值为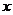 万元(
万元(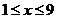 ),农民得到的补贴为
),农民得到的补贴为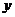 万元,
万元,
则A型号电视机的价值为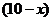 万元,
万元,
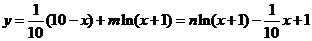
(1)当 时,在
时,在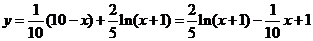
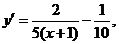
由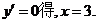
当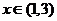 时,
时,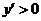 ,
,
当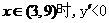
所以当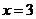 时,
时,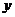 取最大值,
取最大值,
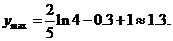
即厂家分别投放A、B两型号电视机7万元和3万元时,农民得到补贴最我,最多补贴约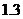 万元。
4分
万元。
4分
(2)由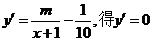
得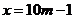
①当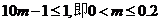 时,
时,
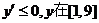 是减函数
是减函数
随B型电视机投放金额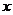 万元的增加,农民得到的补贴逐渐减少。
万元的增加,农民得到的补贴逐渐减少。
②当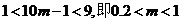 时,
时,
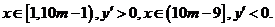
当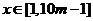 随B型电视机投放金额
随B型电视机投放金额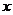 的增加,农民得到的补贴逐渐增加。
的增加,农民得到的补贴逐渐增加。
当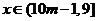 随B型电视机投放金额
随B型电视机投放金额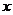 的增加农民得到的补贴逐渐减少。
的增加农民得到的补贴逐渐减少。
③当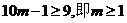 时,
时,
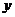 在[1,9]是增函数,随B型电视机投放金额
在[1,9]是增函数,随B型电视机投放金额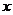 的增加,农民得到的补贴逐渐增加。
的增加,农民得到的补贴逐渐增加。
13分
3.解: (1)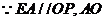 平面ABP
平面ABP
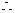 点A、B、P、E共面
点A、B、P、E共面
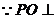 平面ABCD,
平面ABCD,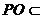 平面PEAB。
平面PEAB。
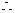 平面PEAB
平面PEAB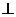 平面ABCD,
平面ABCD,
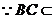 平面ABCD,BC
平面ABCD,BC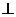 AB
AB
平面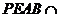 平面ABCD=AB
平面ABCD=AB
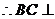 平面PEAB,
平面PEAB,
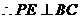
由平面几何知识知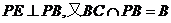
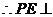 平面PBC 4分
平面PBC 4分
(2)点E即为所求的点,即点M与点E重合。
取PB的中点F,连结EF,CF,DE,
由平面几何知识知EF//AB,
且EF=DE,
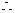 四边形DCFE为平行四边形,
四边形DCFE为平行四边形,
所以DE//CF,
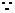 CF在平面PBC内,DE不在平面PBC内,
CF在平面PBC内,DE不在平面PBC内,
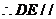 平面PBC。 8分
平面PBC。 8分
(3)由已知可知四边形BCDO是正方形, 显然OD,OB,OP两两垂直;
如图建立空间直角坐标系,
设CD=1,则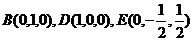 ,
,
设平面BDE的一个法向量为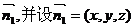
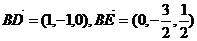
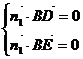
即
取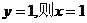
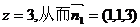
取平面ABD的一个法向量为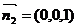
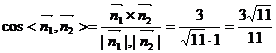
故二面角E-BD-A的余弦值为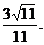
2.解:(1)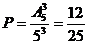 6分
6分
(2)三个区选择的疫苗批号最大数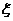 所有可能的取值为1,2,3,4,5
所有可能的取值为1,2,3,4,5
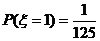 ,
,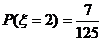
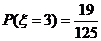 ,
,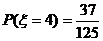
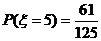
 12分
12分
1.(本题满分12分)
解: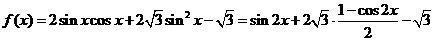
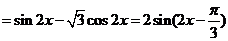
(1)令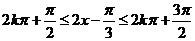
解得单调递减区间是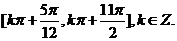
(2)
根据三角函数图像性质可知
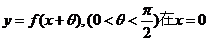 处取最值。
处取最值。
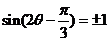
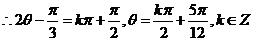
又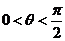
解得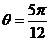 12分
12分
6.(本小题满分13分)
已知焦点在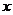 轴上,中心在坐标原点的椭圆C的离心率为
轴上,中心在坐标原点的椭圆C的离心率为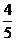 ,且过点
,且过点
(1)求椭圆C的方程;
(2)直线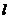 分别切椭圆C与圆
分别切椭圆C与圆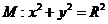 (其中
(其中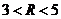 )于A、B两点,求|AB|的最大值。
)于A、B两点,求|AB|的最大值。
华侨中学2010届高三解答题限时训练4答案
5.(本小题满分13分)
各项均不为零的数列 ,首项
,首项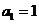 ,且对于任意
,且对于任意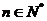 均有
均有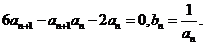
(1)求数列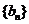 的通项公式;
的通项公式;
(2)若数列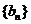 的前
的前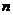 项和为
项和为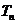
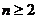 时,
时,
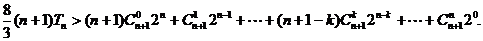
4.(本小题满分13分)
某电视生产厂家有A、B两种型号的电视机参加家电下乡活动。若厂家投放A、B型号电视机的价值分别为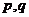 万元,农民购买电视机获得的补贴分别为
万元,农民购买电视机获得的补贴分别为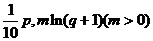 万元。已知厂家把总价值为10万元的A、B两种型号电视机投放市场,且A、B两型号的电视机投放金额都不低于1万元(精确到
万元。已知厂家把总价值为10万元的A、B两种型号电视机投放市场,且A、B两型号的电视机投放金额都不低于1万元(精确到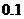 ,参考数据:
,参考数据: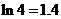 )
)
(1)当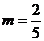 时,请你制定一个投放方案,使得在这次活动中农民得到的补贴最多,并求出其最大值;
时,请你制定一个投放方案,使得在这次活动中农民得到的补贴最多,并求出其最大值;
(2)讨论农民得到的补贴随厂家投放B型号电视机金额的变化而变化的情况。
3.(本小题满分12分)
如图,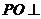 平面ABCD,点O在AB上,EA//PO,四边形ABCD为直角梯形,BC
平面ABCD,点O在AB上,EA//PO,四边形ABCD为直角梯形,BC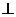 AB,BC=CD=BO=PO,
AB,BC=CD=BO=PO,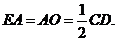
(1)求证:PE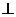 平面PBC;
平面PBC;
 (2)直线PE上是否存在点M,使DM//平面PBC,若存在,求出点M;若不存在,说明理由。
(2)直线PE上是否存在点M,使DM//平面PBC,若存在,求出点M;若不存在,说明理由。
(3)求二面角E-BD-A的余弦值
2.(本小题满分12分)
某市卫生部防疫部门为了控制某种病毒的传染,提供了批号分别为1,2,3,4,5的五批疫苗,供全市所辖的A、B|C三个区市民注射,每个区均能从中任选其中一个批号的疫苗接种。
(1)求三个区注射的疫苗批号互不相同概率;
(2)记A、B、C三个区选择的疫苗批号最大数为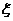 ,求
,求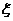 的期望。
的期望。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com