
1.(本小题满分12分)
6.(本小题满分16分)
解:(1)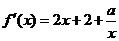
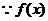 在(0,1)上单调
在(0,1)上单调
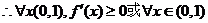
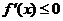 (这是城“=”只对个别
(这是城“=”只对个别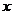 成立)
成立)
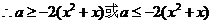
从而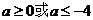 7分
7分
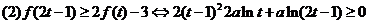 ①
①
令 [
[
则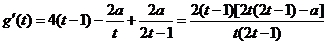
当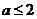 时
时
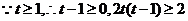
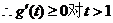 恒成立,
恒成立,
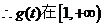 上递增,
上递增,
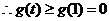 ,即1式对
,即1式对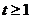 恒成立。
恒成立。
当 时,
时,
令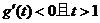 ,
,
解得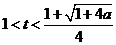
于是,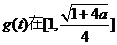 上递减,在
上递减,在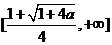 上递增,
上递增,
从而有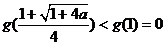 ,即①式不可能恒成立。
,即①式不可能恒成立。
综上所述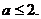
5.(本小题满分14分)
解:(1)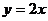 ,
,
设切点分别为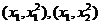
则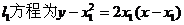
即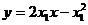 ①
①
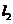 方程为
方程为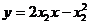 ②
②
由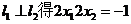
即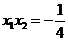
所以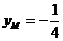 ,即点M的纵坐标为定值
,即点M的纵坐标为定值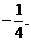
(2)设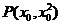 ,
,
则C1在点P处切线方程为: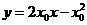
代入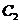 方程
方程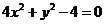
得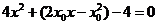
即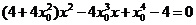
设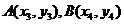
则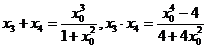
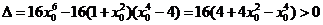 ③
③
由(1)知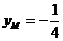
从而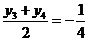 ,
,
即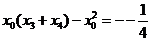
进而得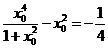 [
[
解得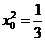 ,且满足③
,且满足③
所以这样点P存在,其坐标为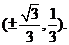 14分[
14分[
4.解:证法1: ∵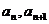 是关于
是关于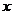 的方程
的方程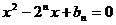
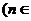 N
N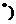 的两根,
的两根,
∴
由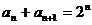 ,得
,得 ,
,
故数列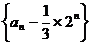 是首项为
是首项为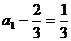 ,公比为
,公比为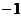 的等比数列.
的等比数列.
证法2: ∵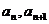 是关于
是关于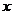 的方程
的方程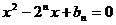
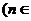 N
N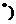 的两根,
的两根,
∴
∵
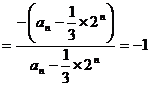 ,
,
故数列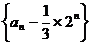 是首项为
是首项为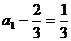 ,公比为
,公比为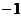 的等比数列.
的等比数列.
(2)解: 由(1)得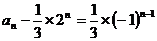 , 即
, 即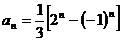 .
.
∴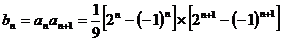
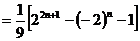 .
.
∴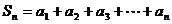
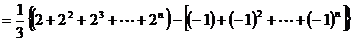
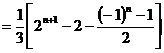 .
.
3.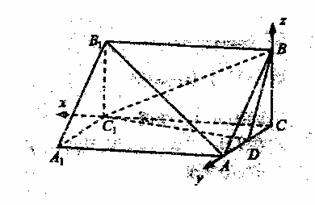 (本小题满分14分)
(本小题满分14分)
解:(1)连接B1C,交BC1于点O,
则O为B1C的中点,
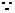 D为AC中点,
D为AC中点,
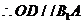 ,
,
又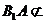 平面BDC1,
平面BDC1,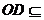 平面BDC1
平面BDC1
 BDC1
4分
BDC1
4分
(2)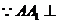 平面ABC,BC
平面ABC,BC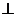 AC,AA1//CC1,
AC,AA1//CC1,
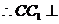 面ABC,数学驿站
面ABC,数学驿站
则BC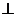 平面AC1,CC1
平面AC1,CC1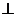 AC
AC
如图建系,则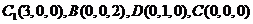
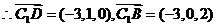
设平面C1DB的法向量为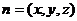
则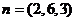
又平面BDC的法向量为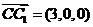
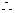 二面角C1-BD-C的余弦值:
二面角C1-BD-C的余弦值:
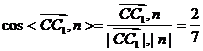 9分
9分
(3)设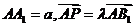 ,
,
则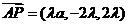

又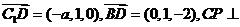 面BDC1,
面BDC1,
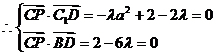
解得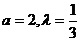
所以AA1=2,点P位置是在线段AB1上且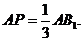 14分
14分
2.(本小题满分14分)
解:(1)不能被4整除的有两种情形;
①4个数均为奇数,概率为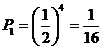 2分
2分
②4个数中有3 个奇数,另一个为2,
概率为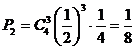 4分
4分
故所求的概率为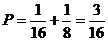 6分
6分
(2)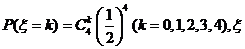 的分布列为
的分布列为
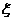 |
0 |
1 |
2 |
3 |
4 |
|
P |
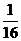 |
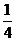 |
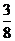 |
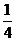 |
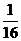 |
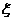 服从二项分布
服从二项分布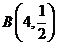 ,
,
则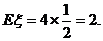 14分
14分
1.(本小题满分14分)
解:由题意得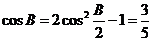
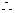 B为锐角,且
B为锐角,且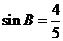 2分
2分
 4分
4分
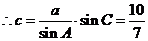 6分
6分
(1)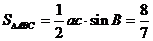 9分
9分
(2) 11分
11分
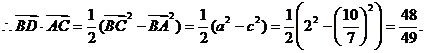 14分
14分
6.(本小题满分16分)
已知函数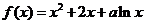
(1)若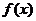 是区间(0,1)上单调函数,求
是区间(0,1)上单调函数,求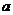 的取值范围;
的取值范围;
(2)若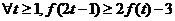 ,试求
,试求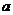
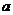 的取值范围。
的取值范围。
华侨中学2010届高三解答题限时训练6答案
5.(本小题满分14分)
已知抛物线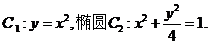
(1)设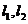 是C1的任意两条互相垂直的切线,并设
是C1的任意两条互相垂直的切线,并设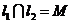 ,证明:点M的纵坐标为定值;
,证明:点M的纵坐标为定值;
(2)在C1上是否存在点P,使得C1在点P处切线与C2相交于两点A、B,且AB的中垂线恰为C1的切线?若存在,求出点P的坐标;若不存在,说明理由。
4.已知数列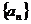 的相邻两项
的相邻两项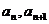 是关于
是关于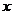 的方程
的方程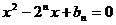
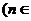 N
N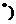 的两根,且
的两根,且
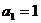 .
.
(1) 求证: 数列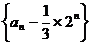 是等比数列;
是等比数列;
(2) 求数列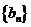 的前
的前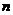 项和
项和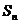 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com